Hemos discutido sobre la teoría de transformador ideal para una mejor comprensión de la realidad elemental teoría del transformador. Ahora vamos a repasar los aspectos prácticos uno por uno de un transformador de energía eléctrica y tratar de dibujar diagrama vectorial del transformador en cada paso. Como dijimos, en un transformador ideal, no hay núcleo pérdidas en el transformador es decir, la pérdida del núcleo libre del transformador. Pero en el transformador práctico, hay histéresis y corriente de remolino pérdidas en el núcleo del transformador.
Teoría del Transformador en No-Carga
No tiene resistencia al devanado y no hay reacción a las fugas
Consideremos una transformador eléctrico con sólo pérdidas de núcleo, lo que significa que sólo tiene pérdidas de núcleo pero no de cobre y no reactancia de fuga del transformador. Cuando se aplica una fuente alternativa en el primario, la fuente suministrará la actual para magnetizar el núcleo del transformador.
Pero esta corriente no es la corriente magnetizadora real, es un poco mayor que la corriente magnetizadora real. La corriente total suministrada por la fuente tiene dos componentes, uno es la corriente magnetizante que se utiliza simplemente para magnetizar el núcleo, y otro componente de la corriente de la fuente se consume para compensar las pérdidas del núcleo en los transformadores.
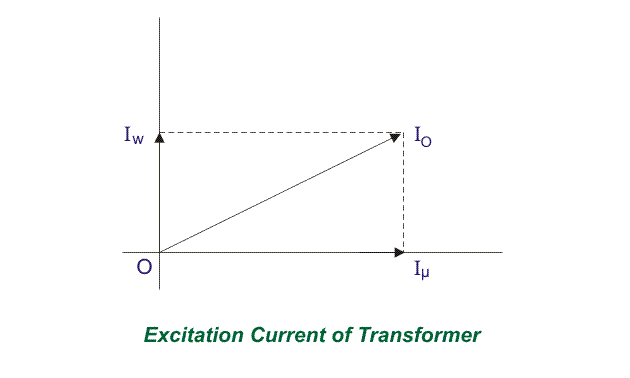
Debido a este componente central de pérdida, la corriente de la fuente en un transformador sin carga condición suministrada por la fuente ya que la corriente de la fuente no está exactamente a 90 lapsos de la tensión de suministro, pero se queda atrás en un ángulo menor de 90o. Si la corriente total suministrada por la fuente es Iotendrá un componente en fase con el suministro voltaje V1 y eles un componentet de la actual Iw es el componente central de la pérdida.
Este componente se toma en fase con el voltaje de la fuente porque está asociado con las pérdidas activas o de trabajo en los transformadores. Otro componente de la corriente de la fuente se denota como Iμ. Este componente produce la alternancia flujo magnético en el núcleo, por lo que no tiene vatios; significa que es una parte reactiva de la corriente de la fuente del transformador. Por lo tanto, yoμ estará en cuadratura con V1 y en fase con flujo alterno. Por lo tanto, la corriente primaria total en un transformador sin carga La condición puede ser representada como:
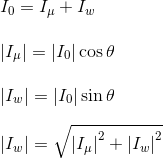
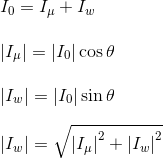
Ahora has visto lo simple que es explicar la teoría del transformador …en sin carga.

Teoría del transformador en carga
No tener resistencia al devanado y reacción a las fugas
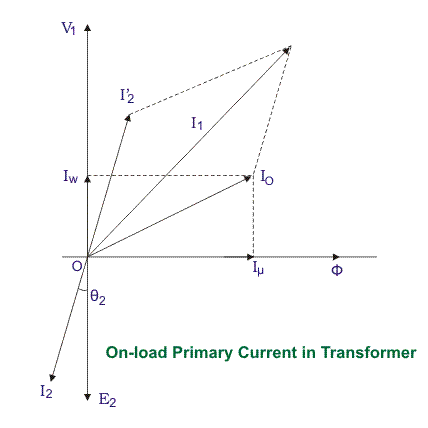

Ahora examinaremos el comportamiento de lo dicho anteriormente transformador en cargaeso significa que la carga está conectada a los terminales secundarios. Considere, un transformador con pérdida de núcleo pero sin pérdida de cobre y reactancia de fuga. Cuando una carga está conectada al bobinado secundario, la corriente de carga comenzará a fluir a través de la carga así como del bobinado secundario.
Esta corriente de carga depende únicamente de las características de la carga y también del voltaje secundario de la transformador. Esta corriente se llama corriente secundaria o corriente de carga, aquí se denota como I2. Como yo.2 está fluyendo a través de la secundaria, un auto mmf en el devanado secundario se producirá. Aquí está N2I2donde, N2 es el número de vueltas del devanado secundario del transformador.


Esta mmf o fuerza magnetomotriz en el devanado secundario produce flujo φ2. Este2 se opondrá al flujo magnetizante principal y debilitará momentáneamente el flujo principal y tratará de reducir la emf E autoinducida primaria1. Si E1 cae por debajo del voltaje de la fuente primaria V1habrá una corriente extra que fluye desde la fuente hasta el devanado primario. Esta corriente extra primaria I2produce un flujo extra en el núcleo que neutralizará el flujo secundario contrario2. Por lo tanto, el principal flujo magnetizante del núcleo, permanece inalterado independientemente de la carga. Así que la corriente total, que este transformador extrae de la fuente puede dividirse en dos componentes. El primero se utiliza para magnetizar el núcleo y compensar la pérdida del núcleo, es decir, Io. Es el componente sin carga de la corriente primaria. La segunda se utiliza para compensar el flujo contrario del devanado secundario. Se conoce como componente de carga de la corriente primaria. Por lo tanto, la corriente primaria total sin carga I1 de un transformador de energía eléctrica sin bobina resistencia y la reactancia de fuga pueden representarse de la siguiente manera
Donde2 es el ángulo entre el voltaje secundario y la corriente secundaria del transformador.
Ahora daremos un paso más hacia un aspecto más práctico de un transformador.
Teoría del transformador en carga, con bobinado resistivo, pero sin reacción de fuga
Ahora, considera la resistencia del bobinado del transformador pero no reactancia de fuga. Hasta ahora hemos discutido sobre el transformador que tiene bobinas ideales, significa bobinas sin resistencia y reactancia de fuga, pero ahora consideraremos un transformador que tiene resistencia interna en el bobinado pero sin reactancia de fuga. Como los devanados son resistivos, habría un voltaje …caen en las bobinas.
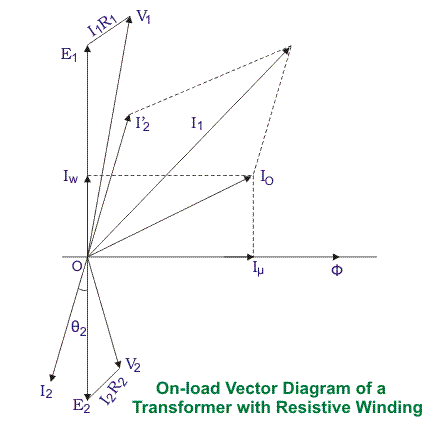

Hemos probado antes que, la corriente primaria total de la fuente en carga es I1. La caída de voltaje en el bobinado primario con resistencia, R1 es R1I1. Obviamente, la EMF inducida a través del devanado primario E1, no es exactamente igual al voltaje de la fuente V1. E1 es menor que V1 por la caída de voltaje I1R1.


De nuevo en el caso del secundario, el voltaje inducido a través del devanado secundario, E2 no aparece totalmente a través de la carga ya que también baja en una cantidad I2R2donde R2 es la resistencia del devanado secundario y yo2 es corriente secundaria o corriente de carga.
De manera similar, el voltaje ecuación del lado secundario del transformador será:


Teoría del Transformador en Carga, con Resistencia así como Reacción de Fuga
Ahora consideraremos la condición, cuando hay una reactancia de fuga del transformador así como la resistencia del devanado del transformador.
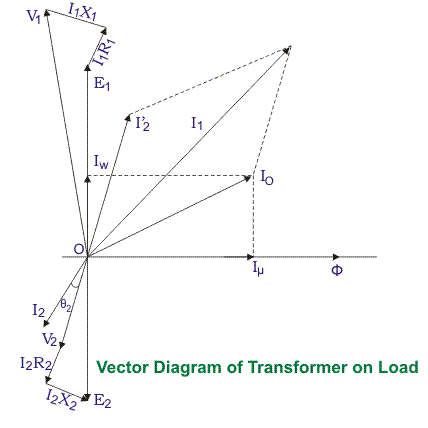

Deje que las reactancias de fuga de los bobinados primarios y secundarios del transformador sean X1 y X2 respectivamente. Por lo tanto, el total impedancia del devanado primario y secundario de transformador con la resistencia R1 y R2respectivamente, puede ser representado como,
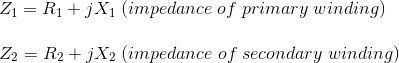
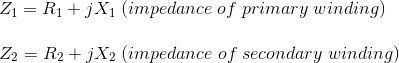
Ya hemos establecido la ecuación de voltaje de un transformador en cargacon sólo resistencias en los devanados, donde las caídas de tensión en los devanados ocurren sólo debido a la caída de tensión resistiva.
Pero cuando consideramos las reactancias de fuga de los devanados de los transformadores, la caída de tensión se produce en el devanado no sólo debido a resistencia, pero también debido a la impedimento de transformador bobinas. Por lo tanto, la ecuación de voltaje real de un transformador puede determinarse fácilmente reemplazando las resistencias R1 & R2 en las ecuaciones de voltaje previamente establecidas con Z1 y Z2.
Por lo tanto, las ecuaciones de voltaje son,
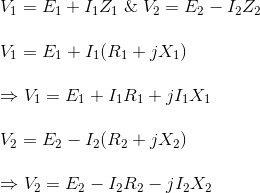
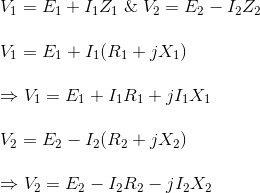
Las caídas de resistencia están en la dirección del vector de la corriente. Pero una gota reactiva será perpendicular al vector de corriente, como se muestra en el anterior diagrama vectorial del transformador.