

¿Cuál es el Principio de Incertidumbre de Heisenberg
El El principio de incertidumbre de Heisenberg es uno de los resultados más interesantes y consecuentes de la naturaleza estadística de la mecánica cuántica. La realización más famosa del principio de incertidumbre afirma que no se puede medir con absoluta certeza la posición y el impulso de un sistema cuántico. Esta es la realización más común y en toda la ciencia popular. Sin embargo, el principio de incertidumbre es mucho más generalizado que esto. El principio de incertidumbre total también se caracteriza por la desigualdad. El principio de incertidumbre generalizada se expresa como:
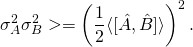
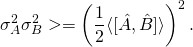
Sólo un caso especial de esta relación generalizada se aplica a la posición y el impulso que atrae la mayor atención. En este artículo, exploraremos lo que significa medir algo, el principio de incertidumbre, y finalmente, el principio de incertidumbre de Heisenberg.
El El principio de incertidumbre de Heisenberg es una consecuencia de la naturaleza estadística de la mecánica cuántica. Para entenderla, primero hay que entender la medición.
¿Qué es medición en la física cuántica?
El acto de medición perturba un sistema cuántico. Por ejemplo, si se realizara cualquier medición como en el artículo para medidas eléctricas se perturbaría el sistema eléctrico subyacente de partículas (también se descubriría rápidamente que no se puede medir con absoluta certeza, pero eso se cubrirá en una fecha posterior). La perturbación en el sistema cuántico se debe a que el proceso de medición es en realidad lo mismo que actuar sobre una función de onda del sistema cuántico (que satisface la Ecuación de Schrodinger) con un operador. Una vez que el operador actúa en la función de onda, la función de onda se colapsará en un eigenstate correspondiente a ese operador. ¡Qué bocado! Demos un paso atrás de toda esta jerga y volvamos a los primeros principios.
Vamos a realizar un experimento de pensamiento sobre la efecto fotoeléctrico tratando de medir dónde exactamente en el otro extremo de la ranura la partícula aterrizará (imagina que tienes una regla y estás tratando de medir dónde a lo largo de la 
 el eje de la partícula aterrizará). Uno de los principales resultados de las primeras etapas de la física cuántica fue que las partículas se comportan como ondas. Eso significa que hay una probabilidad no nula de encontrar la partícula en cualquier lugar a lo largo de la
el eje de la partícula aterrizará). Uno de los principales resultados de las primeras etapas de la física cuántica fue que las partículas se comportan como ondas. Eso significa que hay una probabilidad no nula de encontrar la partícula en cualquier lugar a lo largo de la 
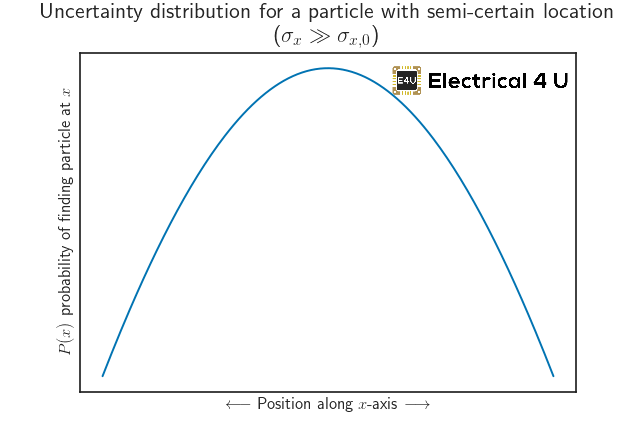
 eje. Veamos algunas distribuciones de probabilidad alrededor de la medición de la posición. Si tuviéramos una idea semicierta de dónde se encuentra la partícula, el error (o la desviación estándar
eje. Veamos algunas distribuciones de probabilidad alrededor de la medición de la posición. Si tuviéramos una idea semicierta de dónde se encuentra la partícula, el error (o la desviación estándar 
 ) de la distribución de las medidas de posición se vería algo así como:
) de la distribución de las medidas de posición se vería algo así como:
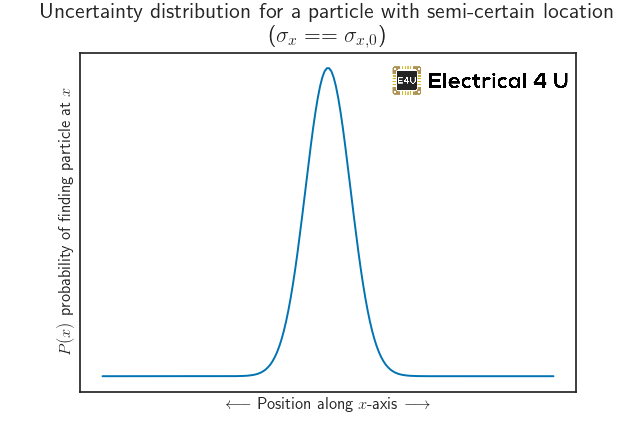

Si de alguna manera supiéramos exactamente dónde se encuentra la partícula a lo largo del eje de posición, la distribución de probabilidad sería algo parecido:
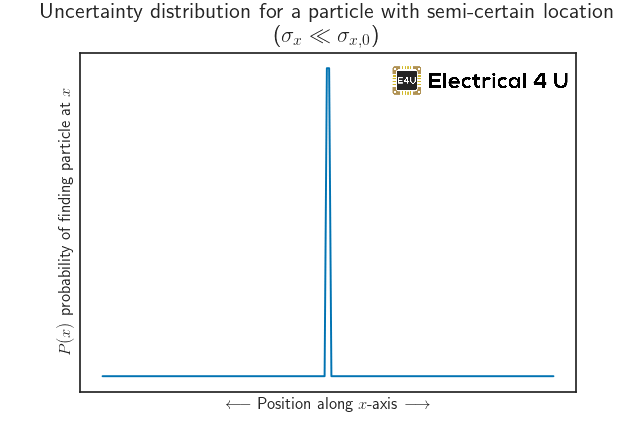

Si tuviéramos poca o ninguna idea de dónde se encuentra la partícula en el otro extremo de la rendija, la distribución de probabilidad sería algo parecido:

Aquí es donde la naturaleza estadística de la mecánica cuántica entra en juego. Cualitativamente, la función de onda proporciona una distribución de probabilidad para cada observable que queramos medir (piensa en la energía, el momento, la posición, la energía total, etc.).
Derivando el principio de incertidumbre de Heisenberg
La derivación de la fórmula de la incertidumbre generalizada se tratará más adelante. El primer hito teórico tiene que ver con la comprensión de que cada vez que se va a realizar una medición, un operador actúa sobre el vector de estado que representa el sistema cuántico. Para la posición, el operador se da como (donde el sombrero implica que es un operador):


Así que cuando se mide la posición de un sistema cuántico, se multiplica el estado por 
 . Para el impulso, el operador parece:
. Para el impulso, el operador parece:
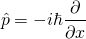
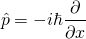
Aquí es donde entra en juego la conversación sobre observables incompatibles. Cada vez que los operadores asociados a los observables tienen un conmutador distinto de cero, no se pueden observar ambos con certeza. El conmutador para dos operadores se define de la siguiente manera:
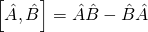
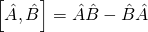
Este conmutador de los dos operadores correspondientes a los observables que intentamos medir se sostiene por la fórmula del principio de incertidumbre generalizada. Ahora vamos a calcular el conmutador para la posición y el momento:
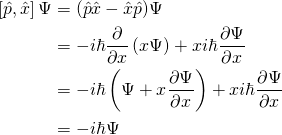
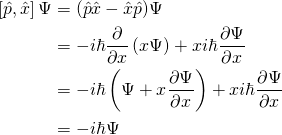
Por lo tanto, si se sustituye este resultado en la fórmula del principio de incertidumbre generalizada, se obtiene el famoso principio de incertidumbre de Heisenberg:
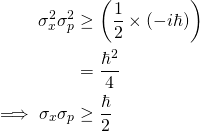
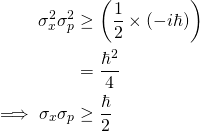
Esta es la famosa realización del principio de incertidumbre. Puede ser interpretado como sigue: a medida que te vuelves más y más seguro acerca de la ubicación de tu sistema cuántico (es decir. 
 más incierto se volverá sobre el impulso del sistema (es decir.
más incierto se volverá sobre el impulso del sistema (es decir. 
 y viceversa. Una vez más, esto se debe al hecho de que la desviación estándar se disparará por el impulso a medida que la desviación estándar por la posición se hace más pequeña (más certidumbre) para mantener el principio de incertidumbre.
y viceversa. Una vez más, esto se debe al hecho de que la desviación estándar se disparará por el impulso a medida que la desviación estándar por la posición se hace más pequeña (más certidumbre) para mantener el principio de incertidumbre.
Citas
- Shankar, R. (1980). Principios de la mecánica cuántica. 1a edición. Nueva York: Springer Science, pp.1-40.
- Gasiorowicz, S. (2019). Física cuántica. 2ª edición. Canadá: Hamilton Printing, pp.1-50.