Teorema de Thevenin
El Teorema de Thevenin dice que un circuito activo entre dos terminales de carga puede ser considerado como una fuente de voltaje individual. El voltaje de esta fuente sería un voltaje de circuito abierto a través de los terminales y la impedancia interna de la fuente es la impedancia equivalente del circuito a través de los terminales.
Para entender el Teorema de Thevenin tomemos un simple ejemplo de un circuito activo resistivo como el que se muestra a continuación.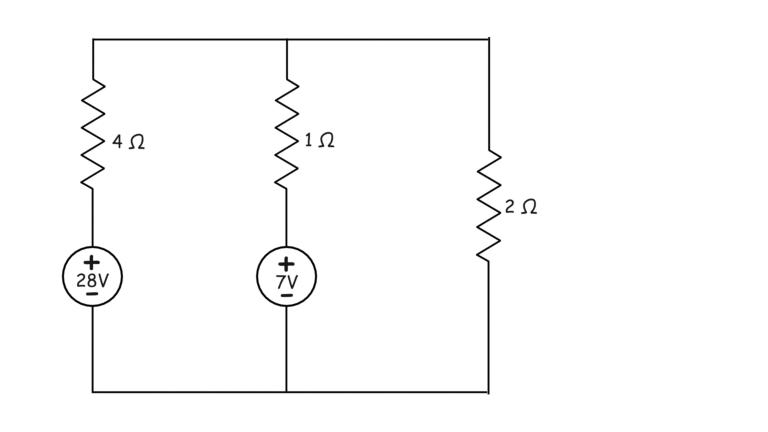
Aquí primero desconectaremos la carga del circuito y luego mediremos el voltaje a través de los terminales del circuito. Este voltaje de circuito abierto a través de los terminales será el voltaje de la fuente si pensamos que todo este circuito es una fuente de voltaje. Este voltaje de circuito abierto también se conoce como voltaje de Thevenin.
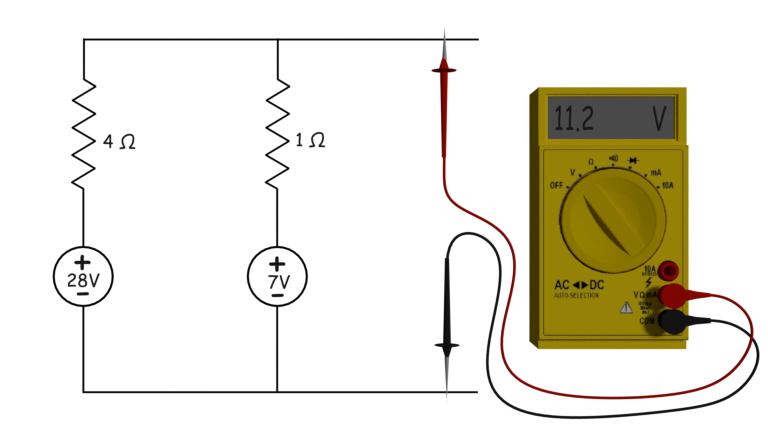
Ahora mediremos la resistencia entre los terminales.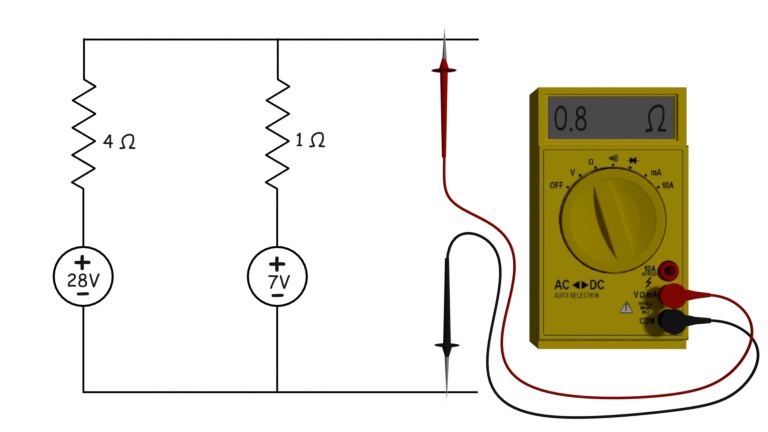
Matemáticamente se puede hacer reemplazando las fuentes individuales con su resistencia interna. En el caso de una fuente de voltaje ideal, podemos hacerlo reemplazando la fuente de voltaje individual por un cortocircuito.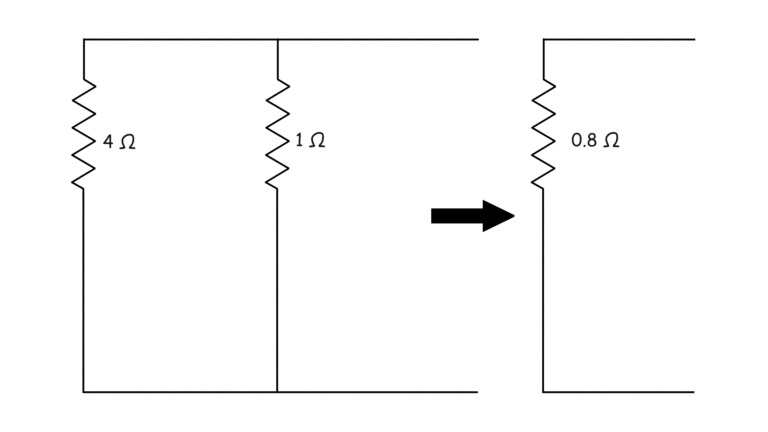 
La resistencia equivalente medida o calculada del circuito a través de los terminales se llama resistencia equivalente de Thevenin.
Todo el circuito activo o red es una fuente de tensión de Thevenin con la resistencia de Thevenin conectada en serie con ella.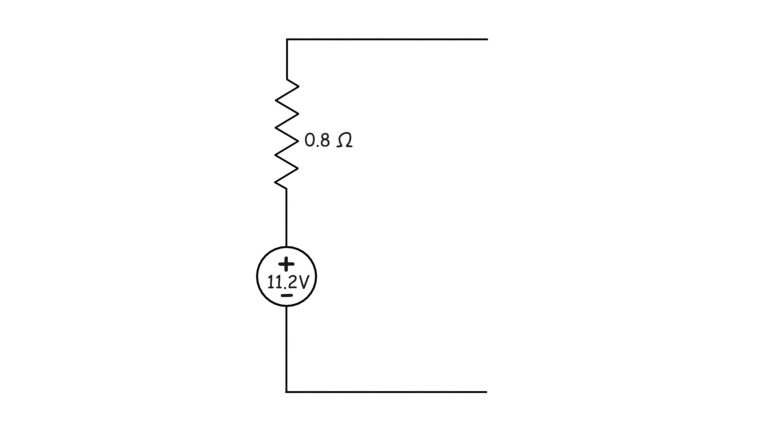
El teorema de Thevenin en un circuito que contiene una fuente de corriente
Aquí la fuente de corriente se convierte primero en una fuente de voltaje equivalente y luego podemos calcular fácilmente el voltaje del circuito abierto o el voltaje de Thevenin y la resistencia del circuito y podemos dibujar la fuente de voltaje de Thevenin equivalente.
No hay nada extra para discutir el Teorema de Thevenin como es tan simple.
El mismo teorema también puede aplicarse para el circuito activo de CA, donde tenemos que tratar con la impedancia en lugar de la resistencia.
Después de revisar los siguientes ejemplos podemos entender mejor el teorema.
Aplicando el Teorema de Thevenins en el circuito de abajo, averigua la corriente de carga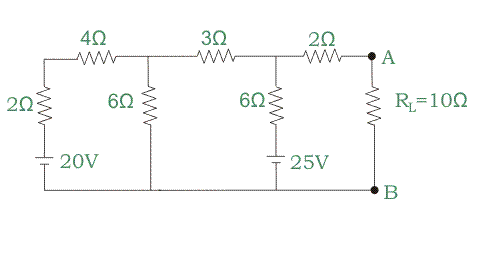
Ahora sigue los pasos uno por uno.
Paso 1: Dibuja el circuito quitando la resistencia de la carga, acortando las fuentes de voltaje y abriendo las fuentes de corriente (si las hay) del circuito. Nombrar los terminales de carga con A y B.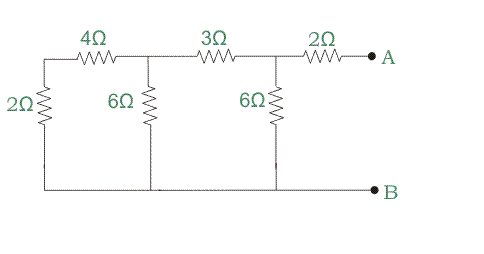
Paso 2: Ver de nuevo en la red de circuito abierto, es decir, desde los terminales abiertos A y B. Calcular la resistencia equivalente del circuito, es decir, RTh.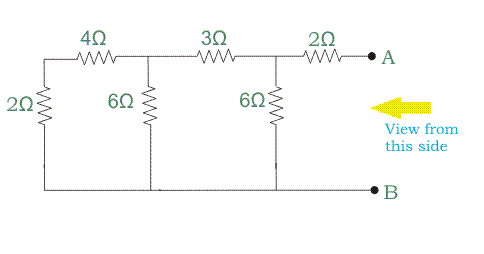
Ahora calcula la resistencia interna de la red.
Tienes el valor de RTh = 5ohm. Del circuito equivalente de Thevenins.
Así que ve a los siguientes pasos para averiguar el valor de VTh.
Paso 3: Dibuja el circuito como antes, pero manteniendo la resistencia de carga eliminada de los terminales A y B.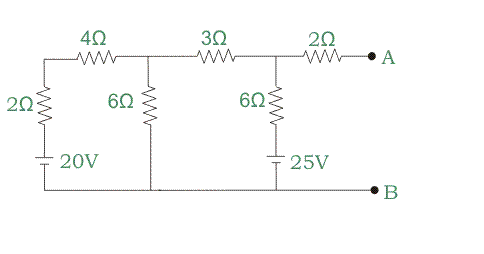
Paso 4: Encuentra los bucles individuales. Aplica la KVL (Ley de voltaje de Kirchhoffs) y encuentra la corriente de los lazos.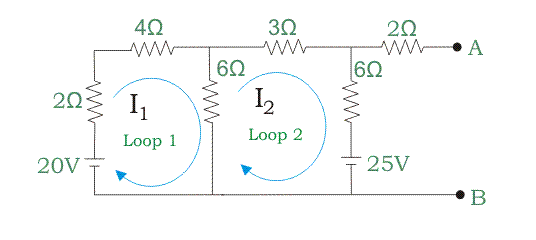
Tienes dos bucles individuales del circuito. Marque los lazos con una flecha en sentido horario como la dirección de la corriente que fluye.
Ahora empieza a aplicar KVL en el primer bucle.
[ya que estás en el bucle 1, considera que yo1 > I2a través de una resistencia de 6 ohmios (I1 I2) la corriente fluirá en]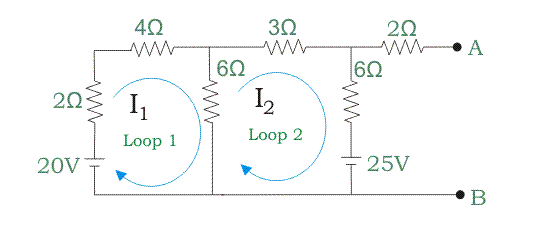
Aplicando KVL en el segundo bucle, conseguimos
[Como estás en el circuito 2, considera que yo2 > I1a través de una resistencia de 6 ohmios (I2 I1) la corriente fluirá en]
Resolviendo dos ecuaciones obtenemos el valor de I1 = 1.041A y I2 = 1.25 A.
Así que la dirección real de la corrientes está marcado en la figura de abajo.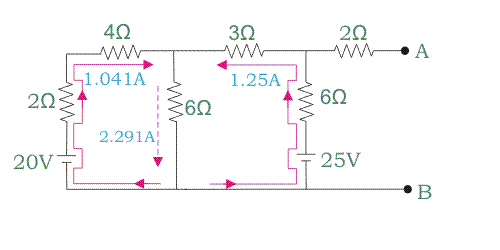
Paso 5: Comienza el viaje desde la terminal A a la B eligiendo cualquier camino de ramas. Calcule el voltaje total al que se ha enfrentado durante el viaje. Este voltaje es VTh.
Supongamos que esta VTh conectados a través de las terminales A y B.
Desde la terminal A comience su viaje por cualquier ramal para llegar a la terminal B.
Comencemos el viaje según el camino marcado por el color rojo.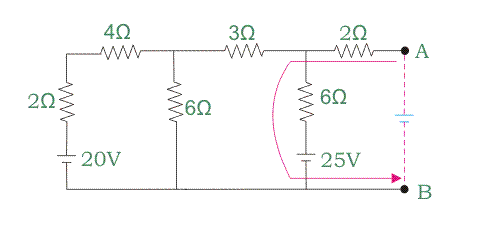
Ahora, aplicando KVL de nuevo, podemos escribir que
[No hay corriente a través de la resistencia de 2 ohmios que acaba de ser conectada al terminal A]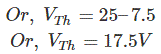
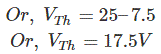
Así que el voltaje de Thevenins VTh es 17.5V.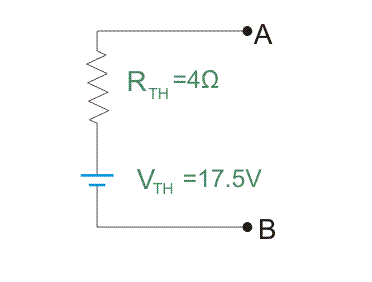
Puede verificar este valor de VTh eligiendo otro camino en el circuito de la terminal A a la B.
Elijamos otro camino según el dibujo de abajo.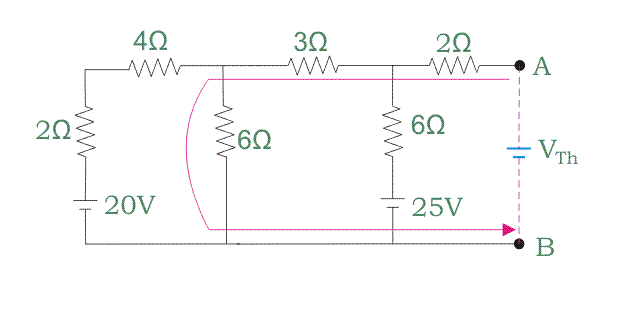
Ahora aplicando la KVL, obtenemos
[no hay corriente a través de la resistencia de 2 ohmios que acaba de ser conectada al terminal A]
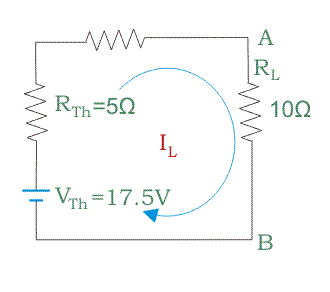
Paso 6: Dibuja el circuito equivalente de Thevenins con el valor de cálculo RTh y VTh. Conecta RL a través de la terminal AB. Aplique de nuevo KVL para averiguar la corriente de carga IL o poner directamente el valor de VTh, RTh y RL en la fórmula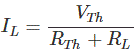
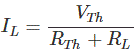
Ahora conecta RL = 10 ohmios a través de la terminal A y B.
De nuevo, aplica. KVL aquí y conseguir
Aplicación del teorema de Thevenins en el sistema de CA
Para calcular la VTh y ZTh tenemos que seguir los pasos que se siguen en el sistema de DC para resolver un problema. Pero una cosa más, es la consideración del ángulo de fase en el sistema de CA.
Empecemos a resolver un problema y familiaricémonos de nuevo con los pasos.
Supongamos que el circuito es como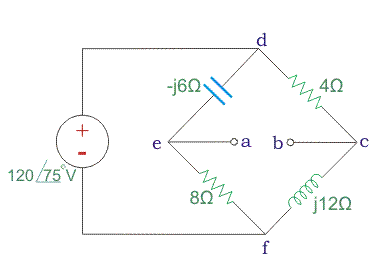
Aquí las terminales A y B son terminales de carga.
Paso 1: Dibuja el circuito quitando la resistencia de la carga, acortando las fuentes de voltaje y abriendo las fuentes de corriente del circuito.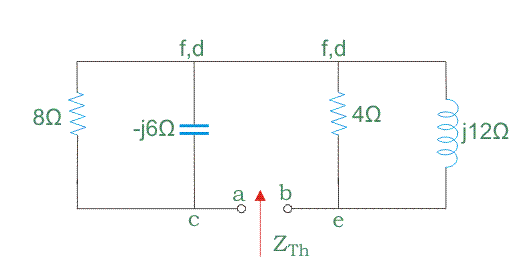
Paso 2: Ver de nuevo en la red de circuito abierto, es decir, desde los terminales abiertos A y B. Calcular la resistencia equivalente del circuito, es decir, ZTh
Paso 3: Dibuja el circuito como antes, pero manteniendo la resistencia de carga eliminada de los terminales A y B.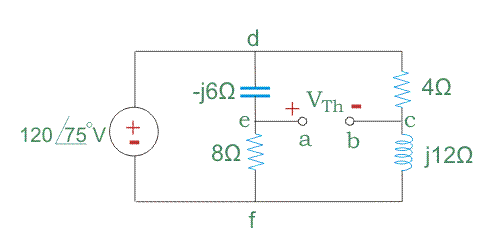
Paso 4: Encuentra los bucles individuales. Aplica la KVL (Ley de voltaje de Kirchhoffs) y encuentra la corriente de los lazos.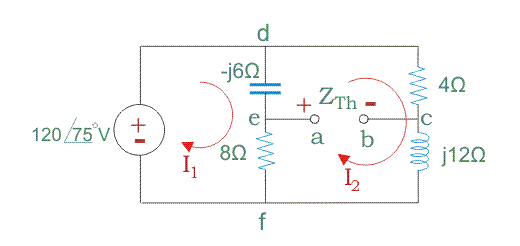
Para el bucle 1,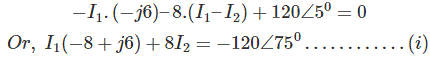
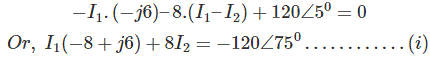
Para el bucle 2,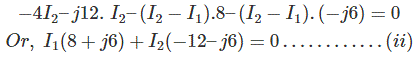
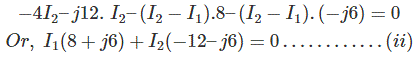
Resolviéndolos conseguimos,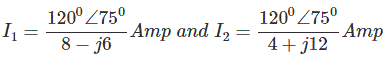
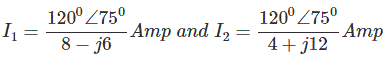
Paso 5: Comienza el viaje desde la terminal A a la B eligiendo cualquier camino de ramas. Calcule el voltaje total al que se ha enfrentado durante el viaje. Este voltaje es VTh.
Elija un camino marcado en rojo en la figura de abajo.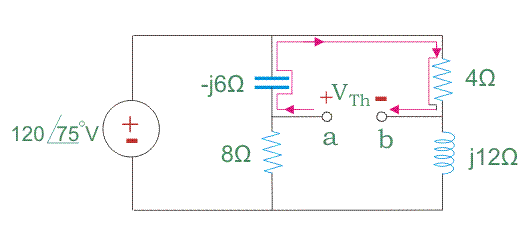
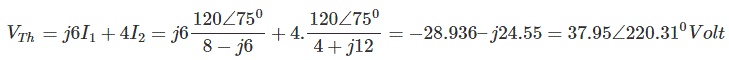
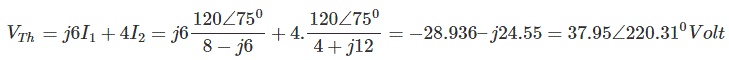
Un problema especial considerando la inducción mutua en el circuito
Sin ninguna inducción mutua, la aplicación del teorema de Thevenin es fácilmente aplicable para averiguar VTh y ZTh. Pero cuando existe el efecto de la inducción mutua en el circuito, entonces un enfoque especial a ser considerado junto con los pasos generales.
Este tipo de circuito se da a continuación.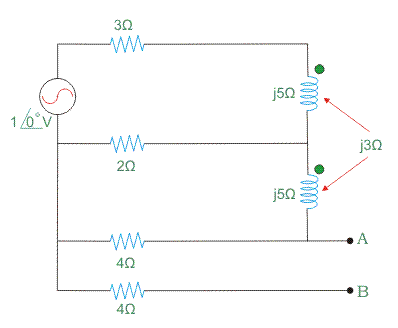
Primero dibuja este circuito según la presencia de inducción mutua.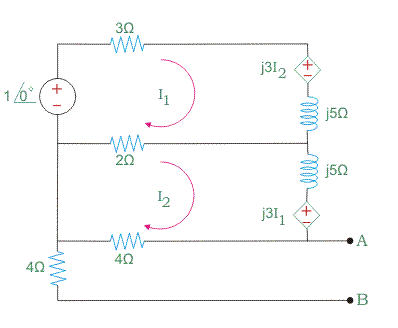
Ahora sigue los pasos uno por uno. Pero surgirá un problema para averiguar que ZTh.
Pero el método más corto y fácil es conectar una fuente de voltaje de 1 voltio a través de los terminales A y B y quitar las fuentes de voltaje del circuito.
Ahora aplica KVL en cada bucle. Por lo tanto, calcula el valor de I3 sólo.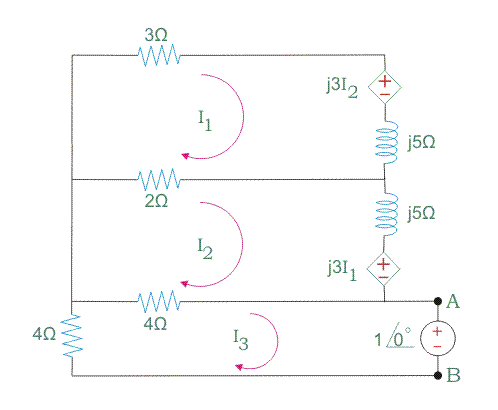
Ahora el valor de ZTh = -1∠0o/I3 ohm.
Pero para averiguar VTh sólo necesitas calcular el valor de I3 del circuito dado abajo.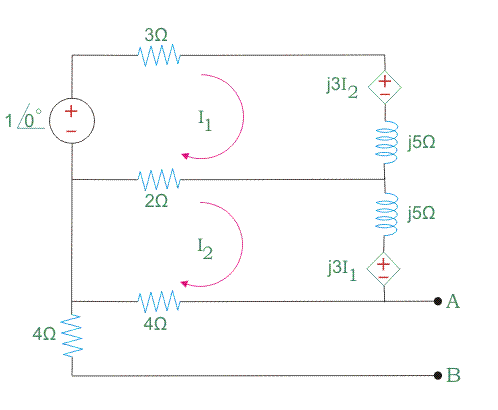
Ahora calcula el valor de I2.
VTh = I20,4 voltios.
Así que obtienes los datos del circuito equivalente de Thevenin.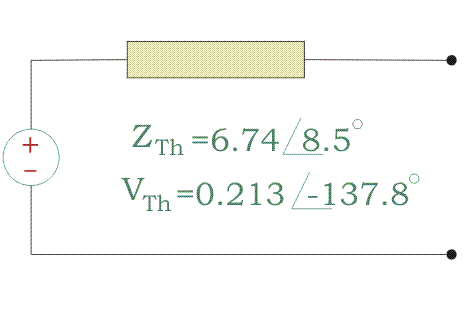
Ejemplo del Teorema de Thevenin
Para los que prefieran una explicación en vídeo, el siguiente vídeo muestra un ejemplo del Teorema de Thevenins en la práctica.
