Si hay varias fuentes que actúan simultáneamente en un circuito eléctrico, entonces la corriente a través de cualquier rama del circuito es la suma de las corrientes que fluirían a través de la rama para cada fuente manteniendo todas las otras fuentes muertas.
Entendamos la declaración.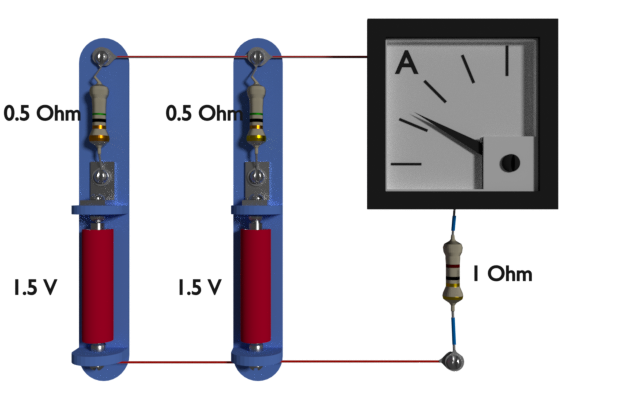

Aquí, dos baterías de 1,5 voltios presentes en el circuito. En esta condición, el actual a través de una resistencia de 1 ohmio es de 1,2 amperios.
El amperímetro indica este valor en la imagen anterior.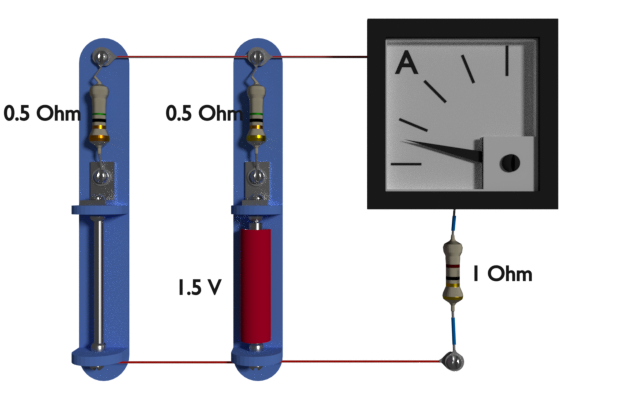

Ahora, reemplazamos el lado izquierdo batería por un cortocircuito como se muestra. En este caso la corriente que fluye a través de la resistencia de 1 ohmio es de 0,6 amperios. El amperímetro indica este valor como se muestra en la imagen de arriba.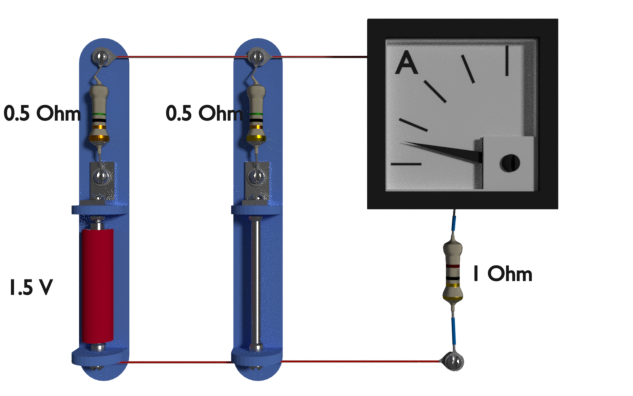

Ahora, reemplazamos la batería del lado derecho por un cortocircuito como se muestra. En este caso la corriente que fluye a través de la resistencia de 1 ohmio es también de 0,6 amperios. El amperímetro indica este valor como se muestra en la imagen de arriba.
1.2 = 0.6 + 0.6
Así que podemos decir que si conectamos una rama de un circuito eléctrico con números de fuentes de voltaje y corriente total actual que fluye a través de esta rama es la suma de todas las corrientes individuales, aportadas por cada fuente individual de voltaje o corriente. Esta simple concepción se representa matemáticamente como Teorema de la superposición.
En lugar de tener dos fuentes como se muestra arriba, hay n número de fuentes que actúan en un circuito debido a que la corriente de I fluye a través de una rama particular del circuito.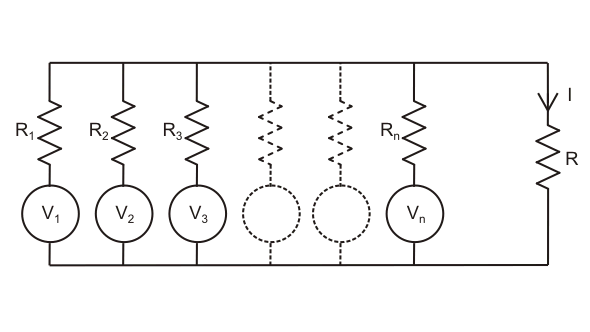

Si alguien reemplaza todas las fuentes del circuito por su resistencia excepto la primera fuente, que ahora está actuando en el circuito y dando corriente I1 a través de dicha rama, luego reconecta la segunda fuente y reemplaza la primera fuente por su resistencia interna.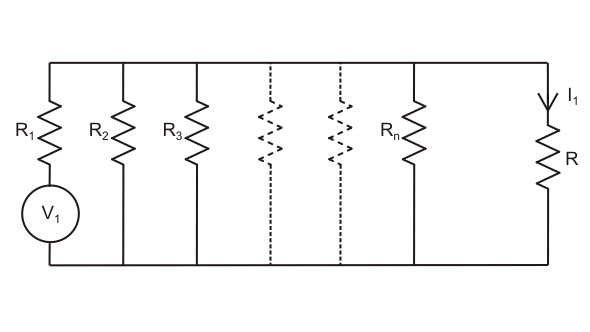

Ahora, la corriente a través de dicha rama para esta segunda fuente solamente puede ser asumida yo2.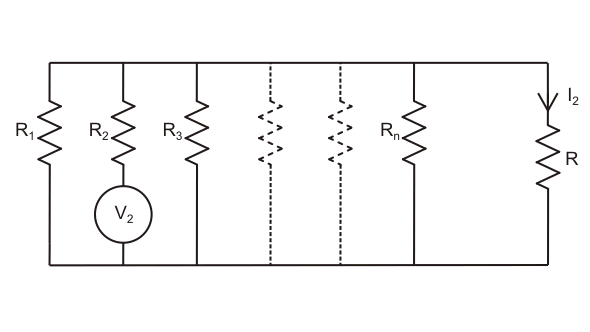

Del mismo modo, si vuelve a conectar la tercera fuente y reemplaza la segunda fuente por su resistencia interna. Ahora la corriente a través de dicha rama para esta tercera fuente, solo se asume que3.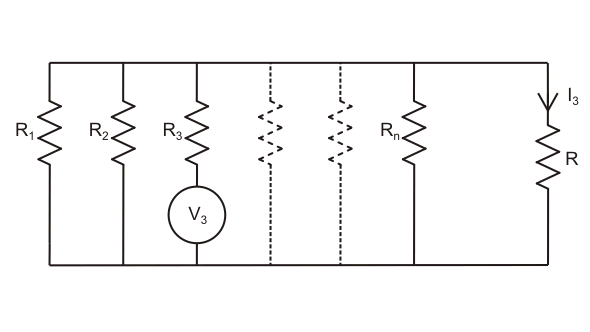

De manera similar, cuando nth la fuente actúa sola en el circuito y todas las demás fuentes son reemplazadas por su resistencias eléctricasentonces dije que yon la corriente fluye a través de dicha rama del circuito.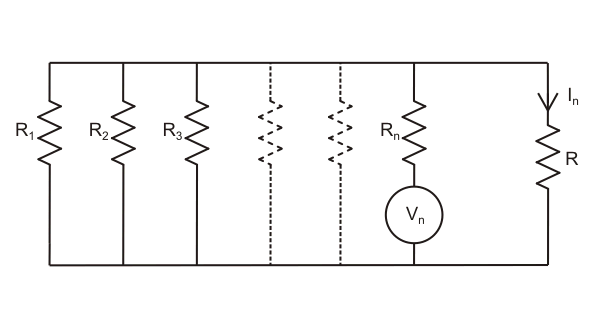

Ahora, de acuerdo con Teorema de la superposiciónla corriente a través de la rama cuando todas las fuentes están actuando en el circuito simultáneamente, no es más que la suma de estas corrientes individuales causadas por las fuentes individuales que actúan solas en el circuito.

Las fuentes eléctricas pueden ser de dos tipos principalmente, una es fuente de tensión y otra es fuente de corriente. Cuando quitamos la fuente de voltaje de un circuito, el voltaje, fue aportado al circuito se convierte en cero. Así que para conseguir el cero diferencia de potencial eléctrico entre los puntos donde la fuente de voltaje retirada fue conectada, estos dos puntos deben ser cortocircuitados por el camino de resistencia cero. Para mayor precisión, se puede reemplazar la fuente de voltaje por su resistencia interna. Ahora, si quitamos una fuente de corriente del circuito, la corriente aportada por esta fuente se convertirá en cero. La corriente cero implica un circuito abierto. Así que cuando quitamos la fuente de corriente de un circuito, sólo desconectamos la fuente de los terminales del circuito y mantenemos ambos terminales en circuito abierto. Como la resistencia interna ideal de una fuente de corriente es infinitamente grande, la eliminación de una fuente de corriente de un circuito puede ser alternativamente referida como el reemplazo de la fuente de corriente por su resistencia. Así que para el teorema de superposición, las fuentes de voltaje son reemplazadas por cortocircuitos y las fuentes s son reemplazadas por circuitos abiertos.
Este teorema sólo es aplicable a un circuito lineal, es decir, un circuito que consiste en resistencias en las que La ley de Ohms es válido. En los circuitos que tienen resistencias no lineales como las válvulas termoiónicas, rectificadores metálicos este teorema no será aplicable. Este teorema es más laborioso que muchos otros teoremas de circuitos. Pero la principal ventaja de este método es que evita las soluciones de dos o más ecuaciones simultáneas. Pero después de un poco de práctica con este método, las ecuaciones pueden escribirse directamente del circuito original y se puede ahorrar el trabajo de dibujar diagramas adicionales. Para una mejor comprensión del procedimiento, hemos proporcionado los diferentes pasos de Teorema de la superposición de la siguiente manera,
Paso 1
Reemplazar todas las fuentes menos una por sus resistencias internas.
Paso 2
Determinar las corrientes en varias ramas usando simples La ley de Ohms.
Paso 3
Repita el proceso usando cada una de las fuentes, vuelta por vuelta, como la única fuente cada vez.
Paso 4
Sume todas las corrientes en una rama particular debido a cada fuente. Este es el valor deseado de corriente en esa rama cuando todas las fuentes actúan en el circuito simultáneamente.
Ejemplo de Teorema de Superposición
Supongamos que hay dos fuentes de tensión V1 y V2 actuando simultáneamente en el circuito.
Debido a estas dos fuentes de voltaje, digamos que la corriente I fluye a través de la resistencia R.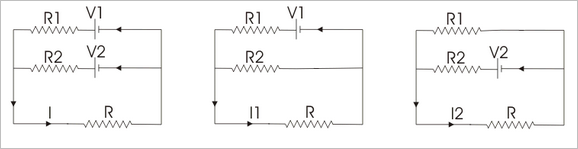

Ahora reemplaza la V2 por un cortocircuito, manteniendo la V1 en su posición y medir la corriente a través de la resistenciaR. Di que soy yo.1.
Entonces reemplace, V1 por un cortocircuito, reconectar V2 a su posición original y medir la corriente a través de la misma resistencia R y decir que es I2.
Ahora, si añadimos estas dos corrientes, yo1 y yo2 obtendremos la corriente que es igual a la corriente que realmente fluía a través de R, cuando ambas fuentes de voltaje V1 y V2 estaban actuando en el circuito simultáneamente. Es decir, yo…1 + I2 = I.