Las funciones de distribución no son más que las funciones de densidad de probabilidad utilizadas para describir la probabilidad con la que una determinada partícula puede ocupar un determinado nivel de energía. Cuando hablamos de Función de distribución del Fermi-Diracestamos particularmente interesados en conocer la posibilidad de encontrar un fermión en un estado energético particular de un átomo (más información sobre esto puede ser encontrada en el artículoEstados de la Energía Atómica). Aquí, por fermiones, nos referimos a los electrones de un átomo que son las partículas con espín, ligadas al principio de exclusión de Pauli.
Necesidad de la función de distribución de Fermi Dirac
En campos como la electrónica, un factor particular de gran importancia es la conductividad de los materiales. Esta característica del material se traduce en el número de electrones que están libres dentro del material para conducir la electricidad.
Según la teoría de la banda de energía (ver el artículoBandas de energía en los cristalespara más información), son el número de electrones que constituyen la banda de conducción del material considerado. Así pues, para tener una idea del mecanismo de conducción, es necesario conocer la concentración de los portadores en la banda de conducción.
Expresión de la distribución de Fermi Dirac
Matemáticamente la probabilidad de encontrar un electrón en el estado de energía E a la temperatura T se expresa como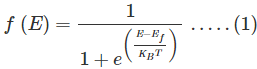
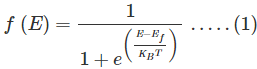
Dónde,
es la constante de Boltzmann
T es la temperatura absoluta
Ef es el nivel de Fermi o la energía de Fermi
Ahora, tratemos de entender el significado del nivel de Fermi. Para lograr esto, pongan
en la ecuación (1). Al hacerlo, obtenemos,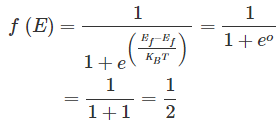
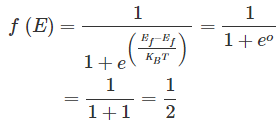
Esto significa que el nivel de Fermi es el nivel en el que se puede esperar que el electrón esté presente exactamente el 50% del tiempo.
Nivel de Fermi en los semiconductores
Semiconductores intrínsecos son los puros semiconductores que no tienen impurezas en ellos. Como resultado, se caracterizan por tener la misma probabilidad de encontrar un agujero que un electrón. Este inturn implica que tienen el nivel de Fermi exactamente entre las bandas de conducción y de valencia como se muestra en la figura 1a.
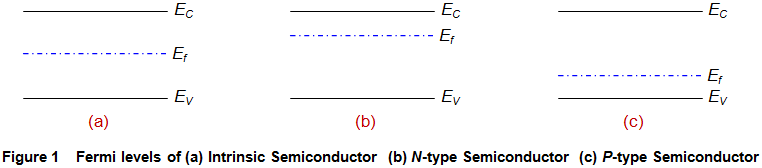

A continuación, considere el caso de un semiconductor tipo n. Aquí, se puede esperar que haya más cantidad de electrones en comparación con los agujeros. Esto significa que hay una mayor posibilidad de encontrar un electrón cerca de la banda de conducción que de encontrar un agujero en la banda de valencia. Por lo tanto, estos materiales tienen su nivel de Fermi localizado más cerca de la banda de conducción como se muestra en la Figura 1b.
Siguiendo con los mismos fundamentos, se puede esperar el nivel de Fermi en el caso de semiconductores tipo p para estar presente cerca de la banda de valencia (Figura 1c). Esto se debe a que estos materiales carecen de electrones, es decir, tienen más agujeros, lo que hace que la probabilidad de encontrar un agujero en la banda de valencia sea mayor en comparación con la de encontrar un electrón en la banda de conducción.
Efecto de la temperatura en la función de distribución del Fermi-Dirac
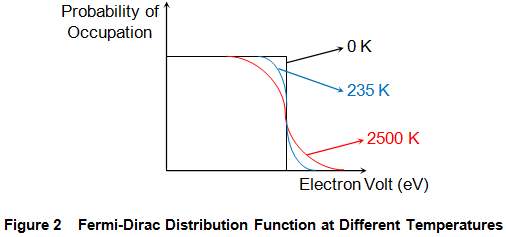

A T = 0 K, los electrones tendrán baja energía y por lo tanto ocuparán estados de energía más bajos. El estado de mayor energía entre estos estados ocupados se denomina nivel de Fermi. Esto significa que ningún estado de energía que esté por encima del nivel de Fermi está ocupado por electrones. Por lo tanto, tenemos una función de paso que define el Función de distribución del Fermi-Dirac como se muestra en la curva negra de la figura 2.
Sin embargo, a medida que la temperatura aumenta, los electrones ganan más y más energía, debido a lo cual pueden incluso subir a la banda de conducción. Así, a temperaturas más altas, no se puede distinguir claramente entre los estados ocupados y los no ocupados, como se indica en las curvas azules y rojas de la figura 2.

