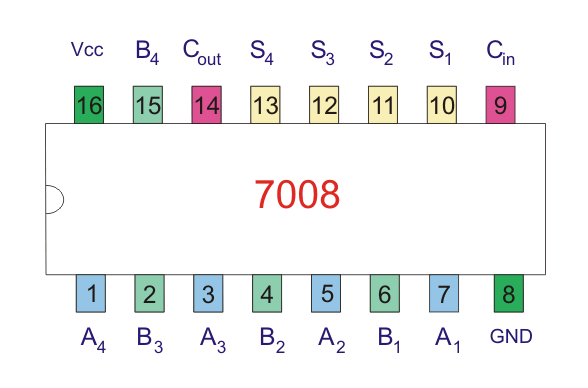
Víbora binaria es uno de los circuitos básicos de lógica combinatoria. Las salidas de un circuito lógico combinatorio dependen sólo de la entrada actual. En otras palabras, las salidas de un circuito lógico combinacional no dependen de ninguna entrada aplicada previamente. No requiere ningún componente de tipo memoria. El sumador binario es uno de los circuitos básicos de lógica combinatoria como estado actual de las variables de entrada.
Diseño de la víbora binaria
Media Víbora
Antes de diseñar un sumador binario, conozcamos algunas reglas básicas de la adición binaria. Las más básicas adición binaria es la adición de dos bits simples números binarios que es la suma de dos dígitos binarios.
Los dígitos binarios son 0 y 1. Por lo tanto, debe haber cuatro combinaciones posibles de adición binaria de dos bits binarios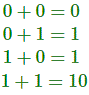
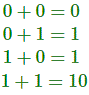
En la lista anterior, las tres primeras operaciones binarias dan como resultado un bit, pero la cuarta da como resultado dos bits. En la suma binaria de un bit, si el aumento y la suma son 1, la suma tendrá dos dígitos. El bit significativo superior (HSB) o el bit del lado izquierdo se llama carry y el bit significativo de la lista (LSB) o el bit del lado derecho del resultado se llama bit de suma. El circuito lógico que realiza esta suma binaria de un bit se llama media víbora.
Diseño de Media Víbora
Para diseñando una media víbora circuito lógico, primero tenemos que dibujar el tabla de la verdad para dos variables de entrada, es decir, los bits de aumento y suma, dos variables de salida llevan y suman bits.
En las tres primeras adiciones binarias, no hay acarreo, por lo que el acarreo en estos casos se considera como 0.
Tabla de la verdad para la media víbora
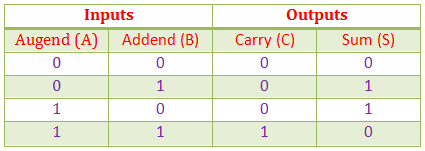

K-map para Half Adder
Ahora desde esta tabla de la verdad podemos dibujar K-map para los cargamentos y las sumas por separado.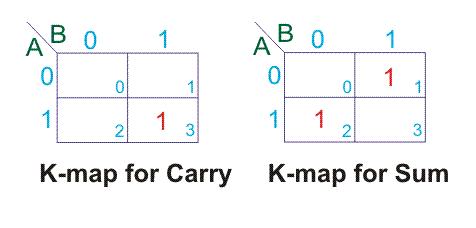

Por encima de los mapas K que tenemos,
Por lo tanto, el diseño lógico de la Media Víbora sería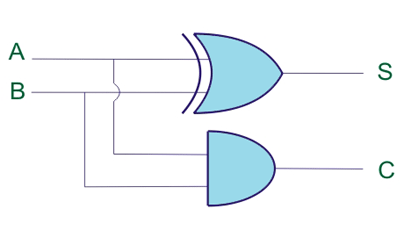

Aunque desde tabla de la verdad se ve claramente que la columna de carga (C) significa Y la operación y la columna de suma (S) significa la operación XOR entre las variables de entrada, pero hasta que pasamos por el K-map como es la práctica general hacerlo para operaciones de lógica binaria más complejas.
Adición completa
Antes de saber acerca de la adición completa, déjanos saber qué es la adición completa… Para eso consideremos el ejemplo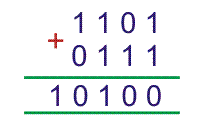

Hay dos números binarios de cuatro bits, 1101 y 0111, que tenemos que añadir. El proceso de adición binaria es como sigue,
- Tenemos que añadir primero el bit significativo de la primera lista (LSB) de ambos números binarios de 4 bits y esto resultará en un número binario de dos bits.


Aquí, los LSB de 1101 y 0111 son 1, por lo tanto 1 + 1 = 10. El LSB de 10 es 0 y el bit significativo superior (HSB) es 1. - El LSB del resultado es la suma y se pondrá en la lista de posición significativa del resultado final de la suma, y el HSB de los dos bits de los resultados se llevará y se sumará con el siguiente bit significativo de dos 4bits augmentar y sumar son 0 y 1 y el llevar de resultado anterior es decir, 1 que se sumará con 0 y 1.
- Después de esta adición, que es la siguiente más alta de la lista de bits significativos de ambos binarios y añadir y es anterior llevar a obtener otro resultado de dos bits. Esto también tiene el acarreo y la suma. Aquí también escribiremos la suma en el resultado final y añadiremos el arrastre a los siguientes bits más significativos del aumento y la suma. Esto continuará hasta la parte más significativa de aumento y suma.
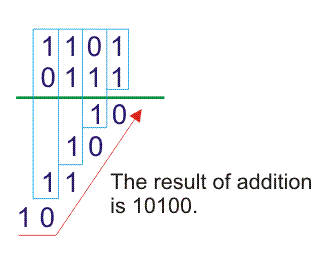

Full Adder
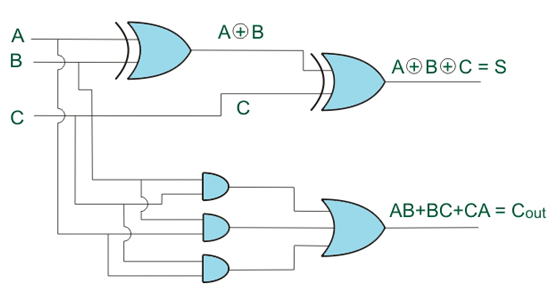
El sumador completo es un circuito condicional que realiza la suma binaria completa, es decir, suma dos bits y un carry y produce un bit de suma y un bit de carry.
Cualquier bit de aumento puede ser 1 o 0 y podemos representar con la variable A, de manera similar cualquier bit de adición que representemos con la variable B. El arrastre después de la adición del mismo bit significativo de aumento y adición puede representar por C. Por lo tanto tabla de la verdad para todas las combinaciones de A, B y C es la siguiente,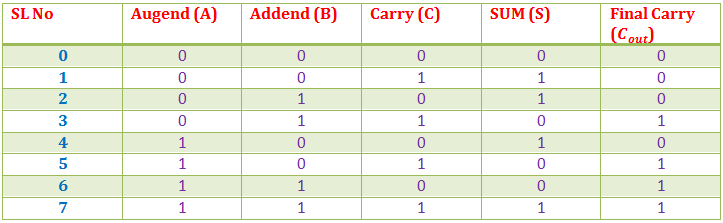

De la tabla anterior, podemos dibujar el mapa K para la suma (s) y el acarreo final (Cfuera).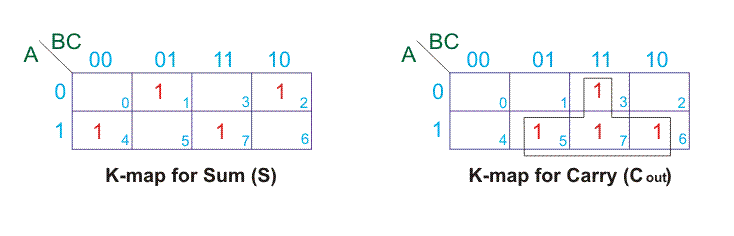

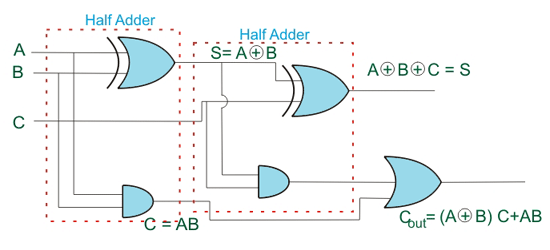
Por lo tanto, de los mapas K,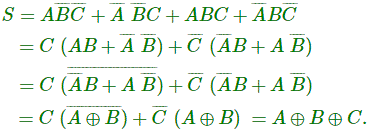
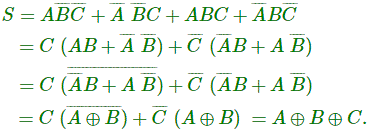

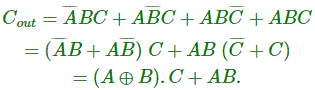
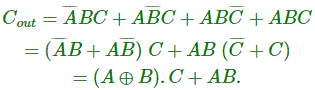

Binary Parallel Adder
Una sumadora binaria completa realiza la adición de cualquier bit individual de un número binario, el mismo significativo o el mismo bit de posición de otro número binario y el transporte proviene del resultado de la adición de los bits anteriores del lado derecho de ambos números binarios. Pero una sola sumadora completa no puede sumar más de un número binario de bits instantáneamente. Esto sólo se puede hacer conectando tantas sumas completas como el número de bits de los números binarios cuya suma se va a realizar. Esta combinación paralela de sumadores completos que realiza la suma de números binarios de bits específicos se llama sumador paralelo binario. Para añadir dos números binarios de 4 bits tenemos que conectar 4 sumadores completos para hacer 4 bits víbora paralela.
A continuación se muestra la interconexión de 4 sumadores completos en sumadores paralelos de 4 bits,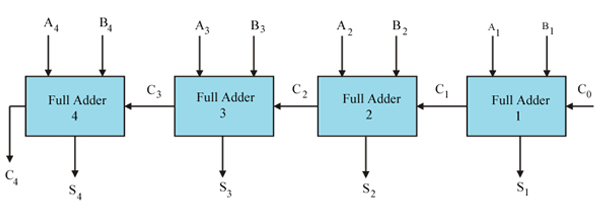

Examinemos la justificación del circuito anterior tomando un ejemplo de adición de dos números binarios de 4 bits.
Añadamos 1011 con 1101.

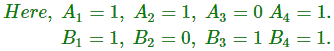
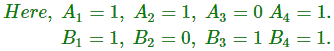
Como no hay una carga previa C0 = 0.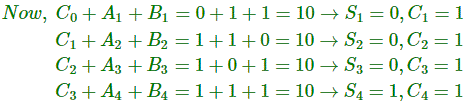
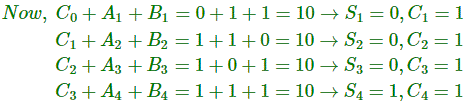
Por lo tanto, el resultado final de la adición sería
Hay 1 bit, 2 bits y 4 bits víboras paralelas Los CI disponibles en el mercado. Para el sumador paralelo de n bits se requiere un número de tales ICs están conectados entre sí.
El IC de 4 bits de la sumadora paralela es 4008. En n bit víbora paralela…el terminal de transporte de salida de un circuito integrado se conectaría con el terminal de transporte de entrada del siguiente circuito integrado.