La entrada y la salida de un red de dos puertos puede ser voltaje o actual. Si la red es impulsada por el voltaje, eso puede ser representado como se muestra a continuación.

Si la red está impulsada por la corriente, eso puede representarse como se muestra a continuación.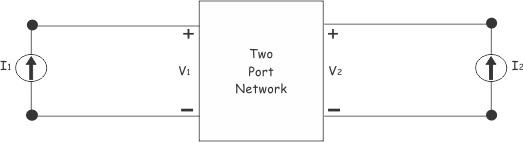

De las dos figuras anteriores, está claro que sólo hay cuatro variables. Un par de variables de voltaje V1 y V2 y un par de variables actuales I1 y yo2. Por lo tanto, sólo hay cuatro relaciones de voltaje a actualy esos son,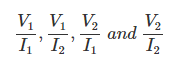
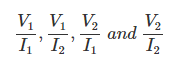
Estas cuatro raciones se consideran como parámetros de la red. Todos lo sabemos,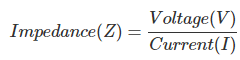
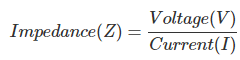
Por eso estos parámetros se llaman parámetro de impedancia o Parámetro Z.
Los valores de estos Parámetro Zs de un red de dos puertospuede ser evaluado haciendo una vez![]()
![]()
y otro una vez![]()
![]()
Expliquémoslo brevemente. Para ello, primero, hacemos que el puerto de salida de la red se abra en circuito abierto como se muestra a continuación.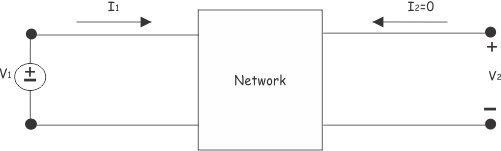

En este caso, como la salida está abierta, no habrá actual en el puerto de salida, es decir.![]()
![]()
En esta condición, la relación de entrada voltaje a la corriente de entrada, se representa matemáticamente como,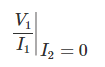
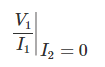
Esto se conoce como impedancia de entrada de la red, mientras que el puerto de salida está abierto. Esto se denota por Z11
Así que, finalmente,

De manera similar,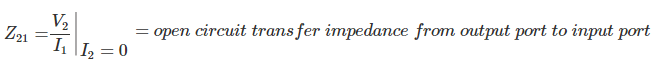
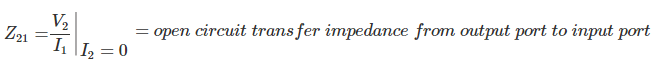
Ahora, Fuente de tensión V2 está conectado a través del puerto 2 que es el puerto de salida, y el puerto 1 o el puerto de entrada se mantiene abierto como se muestra a continuación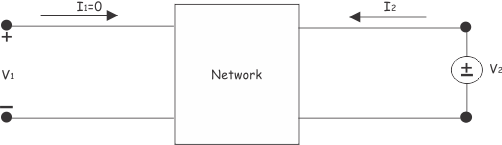

Ahora, la proporción de V2 y yo2 en I1=0 es,![]()
![]()
Esto se llama impedancia de salida de circuito abierto. De manera similar,![]()
![]()
Así,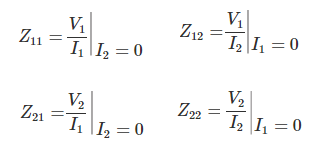
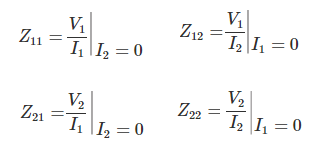
Ya que, todos estos mostrados arriba Parámetro Z se han obtenido por medio de un circuito abierto de puerto de salida o de entrada, los parámetros también se denominan circuito abierto parámetro de impedancia. Ahora, podemos relacionar todos voltaje y las variables actuales de un red de dos puertos por estos Parámetros Z.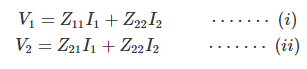
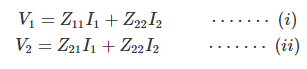
Estas dos ecuaciones pueden ser representadas en forma de matriz, como se muestra a continuación,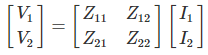
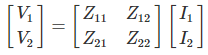
En la ecuación (i), si ponemos I2 = 0, lo conseguimos,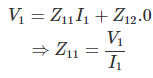
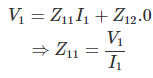
Del mismo modo, si ponemos I1=0, en la misma ecuación, obtenemos,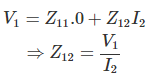
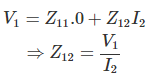
De la misma manera, al poner a I2 = 0 y I1 = 0 alternativamente en la ecuación (ii) Podemos probar,![]()
![]()
Z11 y Z22 también se denominan impedancia del punto de conducción.
Z21 y Z12 también se denominan impedimentos de transferencia. Para una mejor comprensión, tomemos el circuito de abajo,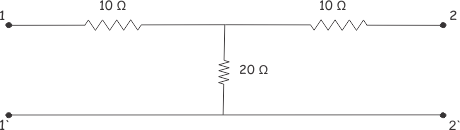

Pongamos un fuente de tensión V1 en la entrada,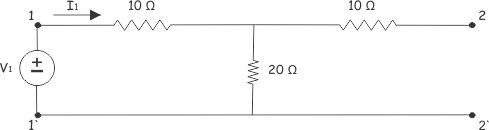

Ahora,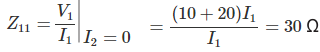
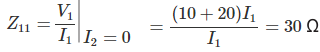
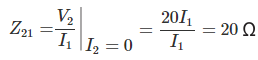
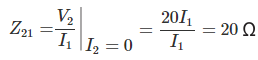
Ahora, conectemos una fuente de voltaje V2 en el puerto de salida y dejar el puerto de entrada tan abierto como se muestra, a continuación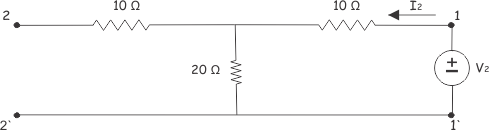

Ahora,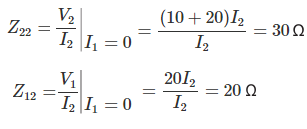
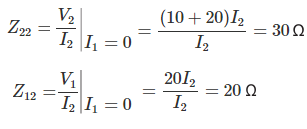
Así que, aquí,![]()
![]()
Cuando en un red de dos puertos…que tenemos,![]()
![]()
Podemos llamarlo red simétrica. Ya que, aquí,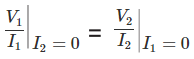
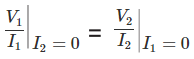
Como esta proporción es la misma, la misma voltaje en cualquiera de los puertos resulta en la misma corrientes en la red. Eso significa que si aplicamos el voltaje V1 en el puerto de salida entonces la corriente de salida será I1. Eso significa que la red tendrá una simetría en forma de espejo entre los puertos de salida y entrada, con respecto a la línea central imaginaria.
Cuando lleguemos,![]()
![]()
Medios,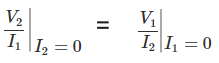
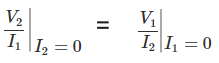
Esto significa que, si la exicación de entrada y la respuesta de salida de la red se intercambian, la impedancia de transferencia permanece igual.
Supongamos que V es el voltaje de entrada y que I es la corriente de salida de la red, como se muestra a continuación.

Ahora bien, si conectamos un fuente de corriente de I en el puerto de entrada, así que el voltaje La respuesta de la red sería, V, en el puerto de salida.

Esto se debe a que la relación entre el voltaje y actual entre la entrada y la salida permanecen iguales en ambas condiciones. Esto es Teorema de la reciprocidad. El red de dos puertos comportarse así se denomina red recíproca.
Para la red simétrica,![]()
![]()
Para la red recíproca![]()
![]()