La suma de dos variables en el sistema binario es así,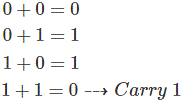
La puerta realiza esta operación de módulo suma sin incluir el transporte se conoce como Puerta XOR. Una puerta XOR es normalmente una puerta lógica de dos entradas donde, la salida es sólo lógica 1 cuando sólo una entrada es lógica 1. Cuando ambas entradas son iguales, es decir, ambas son 1 o ambas son 0, la salida será 0 lógico. Esta es la razón por la que un Puerta XOR también llamado puerta anti-coincidencia o detector de desigualdad. Esta puerta se llama XOR o exclusiva Puerta de la sala de operaciones porque, su salida es sólo 1 cuando una de sus entradas es exclusivamente 1.
El tabla de la verdad de la puerta XOR se da a continuación,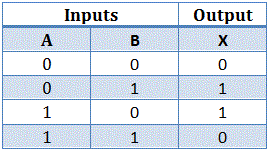

La operación binaria de la tabla de verdad anterior se conoce como operación OR exclusiva y se representa como, A B. El símbolo de la operación OR exclusiva se representa por un anillo de más rodeado por un círculo .
Realización de la puerta XOR de dos entradas
La expresión anterior, A B puede simplificarse como,
Probemos la expresión anterior.
En el primer caso considere, A = 0 y B = 0.
En el segundo caso considere, A = 0 y B = 1.
En el tercer caso considere, A = 1 y B = 0.

En el cuarto caso considere, A = 1 y B = 1.
Así se demuestra que, la expresión booleana para A B es AB + B, ya que esta expresión booleana satisface todos los estados de salida respecto a las condiciones de entrada, de un Puerta XOR.
A partir de esta expresión booleana se puede realizar fácilmente el circuito lógico de una puerta XOR y esto será como un espectáculo,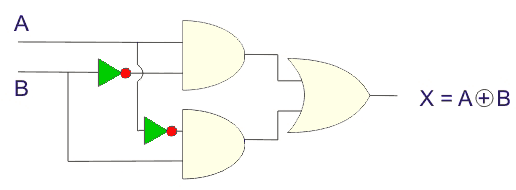

Símbolo lógico de la Puerta XOR
Una puerta XOR se representa lógicamente como,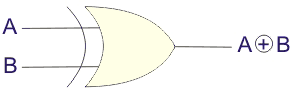

Más de dos entradas Puerta XOR
Como ya dijimos, las puertas XOR son puertas de dos entradas, pero el funcionamiento del XOR de más de dos entradas puede realizarse usando más de una o dos entradas Puerta XOR. El funcionamiento del XOR de más de dos entradas es que, cuando el número impar de entradas en la puerta es 1, la salida es 1 y cuando ninguno o el número par de entradas es 1, la salida es el lógico 0.
Realización de más de dos entradas Puerta XOR
Realicemos una puerta XOR con tres entradas A, B y C.
Ahora, según la definición de la operación XOR con más de tres entradas, el tabla de la verdad sería,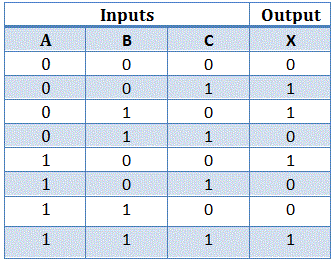

Esta tabla de la verdad puede ser elaborada como,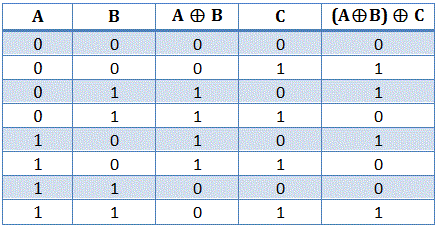

De la tabla de verdad elaborada anteriormente se desprende que, la operación XOR de tres variables binarias es equivalente a, la operación XOR una variable con resultado de operaciones XOR de otras dos variables.
Desde la mesa de la verdad,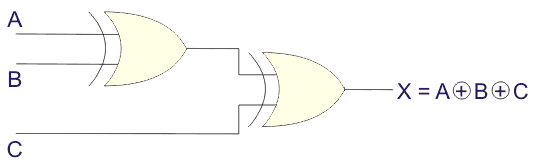

Puerta XNOR
Puerta XNOR es un NO es una puerta seguido de una puerta XOR. Como sabemos que el funcionamiento XOR de las entradas A y B es A B, por lo tanto el funcionamiento XNOR esas entradas serán (A + B) . Eso significa que la salida de la puerta XOR se invierte en la puerta XNOR. En el funcionamiento XOR, la salida es sólo 1 cuando sólo una entrada es 1. La salida es 0 lógico cuando ambas entradas son iguales, es decir, son 1 o 0. Pero en el caso de la puerta XNOR, la salida es 0 cuando sólo una entrada es 0 y la salida es 1 cuando ambas entradas son iguales, es decir, son 0 o 1.
El tabla de la verdad del Puerta XNOR se muestra a continuación,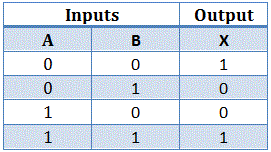

La operación lógica de XNOR está representada por . Es un punto rodeado por un círculo. La expresión de la operación XNOR entre la variable A y B se representa como A B.
Ahora de nuevo, la tabla de la verdad se satisface con la ecuación AB + B .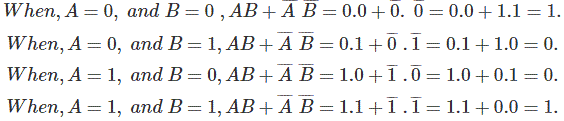
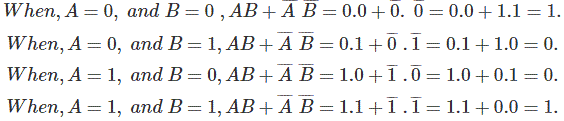
Por lo tanto, se demuestra que A B = AB + B . Lo mismo se puede probar usando K-map también.
Realización de la Puerta XNOR
La expresión de la operación XNOR puede realizarse utilizando dos NO las puertas…dos… Y las puertas y uno Puerta de la sala de operaciones como seguidores,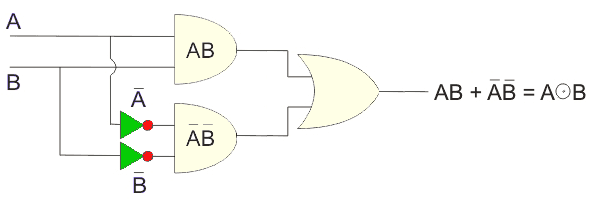

El símbolo de la puerta XNOR.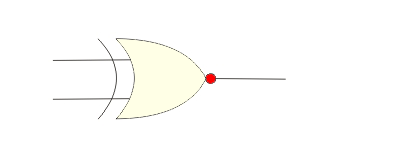

Tres entradas de puertas XNOR
Como Puerta XORLa puerta XNOR sólo existe con dos entradas, pero para el funcionamiento de XNOR con más de dos entradas, tenemos que usar más de una puerta XNOR. El funcionamiento de XNOR con más de dos entradas es así, cuando hay números impares de entradas en condición alta o lógica 1, la salida será 0 en caso contrario la salida será 1.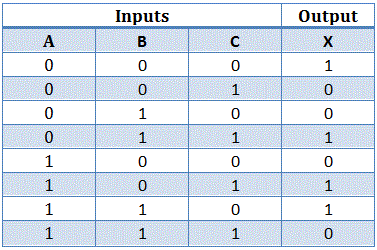

Ahora,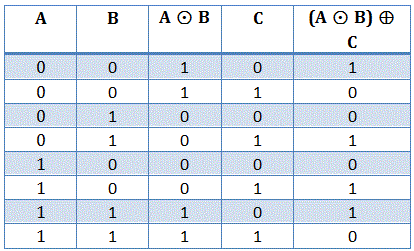

De esta elaborada tabla de la verdad, el símbolo lógico de las tres entradas de la puerta XNOR puede ser representado como,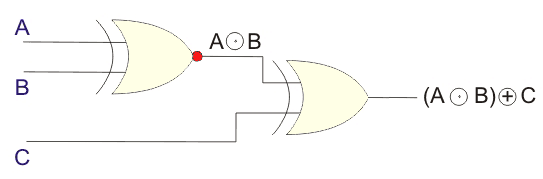

Aplicación de la Puerta XOR
La principal aplicación de la puerta de quirófano exclusiva está en el funcionamiento de media y completa víbora. Si miramos a la tabla de la verdad cuidadosamente encontraremos que los tres primeros resultados son totalmente satisfactorios el proceso de adición binaria pero en la última secuencia de entrada, es decir, cuando ambas entradas son 1, el resultado según la regla de la suma debe ser 0 con una acarreo 1. En la tabla de verdad estamos obteniendo el 0 deseado pero falta un 1.
Para resolver este problema durante el diseño del circuito de un sumador, se añade una puerta Y al Puerta Ex-OR en paralelo. Mostraremos el circuito de la víbora en detalle.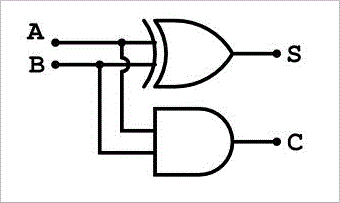

Del diagrama anterior, podemos ver que en el circuito de una media sumadora las dos entradas están pasando por una puerta Exclusiva-OR y por una puerta AND en paralelo. Y con este funcionamiento de los circuitos obtenemos el proceso total de adición binaria sin problemas.
Generación de números pseudo-aleatorios.
Para modelar una retroalimentación lineal registro de cambio Se utilizan puertas Ex-OR y generan una secuencia aleatoria de bits.




