El puente de Wheatstone
Para medir con precisión cualquier resistencia eléctrica El puente de Wheatstone se utiliza ampliamente. Hay dos conocidos resistencias…uno… resistencia variable y una resistencia desconocida conectada en forma de puente como se muestra a continuación. Ajustando la resistencia variable, el actual a través del Galvanómetro se hace cero. Cuando la corriente que pasa por el galvanómetro se convierte en cero, la relación de dos resistencias conocidas es exactamente igual a la relación entre el valor ajustado de la resistencia variable y el valor de la resistencia desconocida. De esta manera el valor de la resistencia desconocida resistencia eléctrica puede ser fácilmente medido usando un puente de Wheatstone.
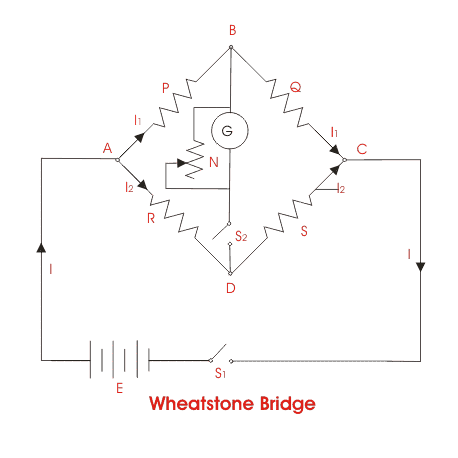

Teoría del puente de Wheatstone
La disposición general de El circuito del puente de Wheatstone se muestra en la siguiente figura. Es un circuito puente de cuatro brazos donde los brazos AB, BC, CD y AD están formados por resistencias eléctricas P, Q, S y R respectivamente.
Entre estas resistencias P y Q se conocen las resistencias eléctricas fijas y estos dos brazos se denominan brazos de relación. Un Galvanómetro preciso y sensible está conectado entre los terminales B y D a través de un interruptor S2.
El fuente de tensión de este El puente de Wheatstone está conectado a los terminales A y C a través de un interruptor S1 como se muestra. A resistencia variable S está conectado entre el punto C y D. El potencial en el punto D puede ser variado ajustando el valor de la resistencia variable. Supongamos que la corriente I1 y la actual I2 están fluyendo a través de los caminos ABC y ADC respectivamente.
Si variamos la resistencia eléctrica valor del brazo CD el valor de la corriente I2 también será variado como el voltaje a través de la A y la C es fijo. Si continuamos ajustando la resistencia variable, puede darse una situación en la que la caída de voltaje a través de la resistencia Es decir, yo…2. S es se convierte en exactamente igual a Caída de tensión a través de la resistencia Q, es decir, yo1Q. Por lo tanto, el potencial en el punto B se convierte en igual al potencial en el punto D, por lo tanto diferencia de potencial entre estos dos puntos es cero, por lo que la corriente a través del galvanómetro es nula. Entonces la desviación en el galvanómetro es nula cuando el interruptor S2 está cerrado.
Ahora, desde El circuito del puente de Wheatstone![]()
![]()
y![]()
![]()
Ahora el potencial del punto B con respecto al punto C no es más que la caída de voltaje a través de la resistencia Q y esto es![]()
![]()
Una vez más, el potencial del punto D con respecto al punto C no es más que el Caída de tensión a través de la resistencia S y esto es![]()
![]()


Al igual que las ecuaciones (i) y (ii) que obtenemos,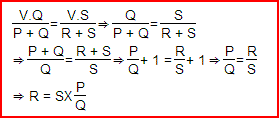
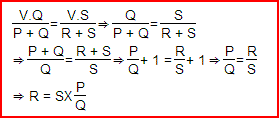
Aquí en la ecuación anterior, el valor de S y PQ son conocidos, por lo que el valor de R puede ser fácilmente determinado.
El resistencias eléctricas P y Q de la El puente de Wheatstone están hechos de una relación definida como 1:1; 10:1 o 100:1 conocidos como brazos de relación y S el brazo del reóstato se hace continuamente variable de 1 a 1.000 o de 1 a 10.000 .
La explicación anterior es muy básica La teoría del puente de Wheatstone.