Teoría del Puente de Schering
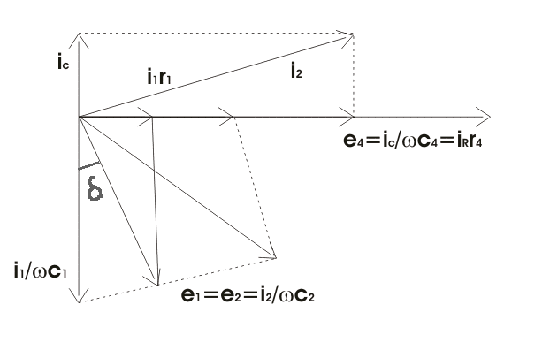
Este puente se utiliza para medir a la capacitancia del condensador, el factor de disipación y la medición de la permitividad relativa. Consideremos el circuito de El puente de Schering como se muestra a continuación: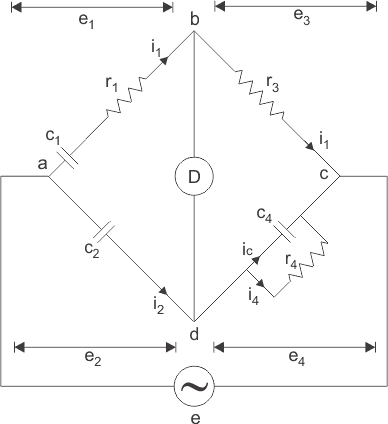
Aquí, c1 es la capacitancia desconocida cuyo valor debe determinarse con la resistencia eléctrica en serie r1.
c2 es un condensador estándar.
c4 es un condensador variable.
r3 es un puro resistencia (es decir, de naturaleza no inductiva).
Y r4 es una resistencia variable no inductiva conectada en paralelo con la variable condensador c4. Ahora el suministro se da al puente entre los puntos a y c. El detector está conectado entre b y d. De la teoría de los puentes ac tenemos en condición de equilibrio,
Sustituyendo los valores de z1, z2, z3 y z4 en la ecuación anterior, obtenemos
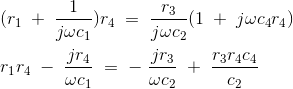
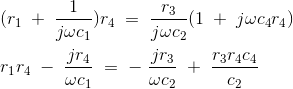
Igualando las partes reales e imaginarias y la separación que obtenemos,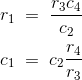
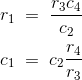
Consideremos el diagrama de fases del circuito del puente de Shering y marquemos el caídas de tensión a través de ab, bc, cd y ad como e1, e3,e4 y e2 respectivamente. A partir del anterior diagrama de fases del puente de Schering, podemos calcular el valor del bronceado, que también se denomina factor de disipación.
La ecuación que hemos deducido anteriormente es bastante simple y el factor de disipación puede ser calculado fácilmente. Ahora vamos a discutir el puente Schering de alto voltaje en detalle. Como hemos discutido, ese simple puente de Schering (que utiliza bajos voltajes) se utiliza para medir el factor de disipación, la capacitancia y la medición de otras propiedades de los materiales aislantes como el aceite aislante, etc. ¿Qué necesidad hay de un puente de schering de alto voltaje? La respuesta a esta pregunta es muy simple, para la medición de la pequeña capacitancia necesitamos aplicar alto voltaje y alta frecuencia en comparación con el bajo voltaje que sufre muchas desventajas. Discutamos más características de este puente Schering de alto voltaje:
- El puente de los brazos ab y ad consiste sólo en condensadores como se muestra en el puente que figura a continuación y las impedancias de estos dos brazos son bastante grandes en comparación con las impedancias de bc y cd. Los brazos bc y cd contienen la resistencia r3 y la combinación paralela del condensador c4 y la resistencia r4 respectivamente. Como las impedancias de bc y cd son bastante pequeñas, por lo tanto, la caída a través de bc y cd es pequeña. El punto c está conectado a tierra, de modo que el voltaje a través de bc y dc están unos pocos voltios por encima del punto c.
- El alto voltaje El suministro se obtiene de una transformador 50 Hz y el detector de este puente es un galvanómetro de vibraciones.
- Las impedancias de los brazos ab y ad son muy grandes, por lo tanto este circuito consume poca corriente y por lo tanto la pérdida de energía es baja, pero debido a esta baja actual necesitamos un detector muy sensible para detectar esta baja corriente.
- El condensador estándar fijo c2 tiene gas comprimido que funciona como dieléctrico, por lo tanto el factor de disipación puede ser tomado como cero para el aire comprimido. Las pantallas de tierra se colocan entre los brazos altos y bajos del puente para evitar errores causados por la inter-capacidad.
Estudiemos cómo el puente Schering mide la permitividad relativa: Para medir la permitividad relativa, necesitamos primero medir la capacitancia de un pequeño condensador con una muestra como dieléctrico. Y a partir de este valor medido de capacitancia la permitividad relativa puede calcularse fácilmente utilizando la relación muy simple:
Donde, r es la permeabilidad relativa.
c es la capacitancia con el espécimen como dieléctrico.
d es el espacio entre los electrodos.
A es el área neta de los electrodos.
y es la permitividad del espacio libre.
Hay otra forma de calcular la permitividad relativa del espécimen cambiando el espaciado de los electrodos. Consideremos el diagrama que se muestra a continuación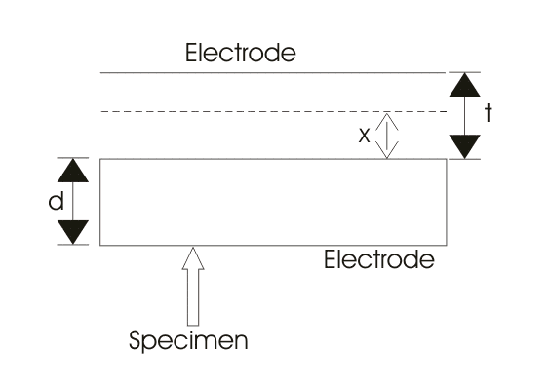
Aquí A es el área de los electrodos.
d es el grosor del espécimen.
t es el hueco entre el electrodo y la muestra (aquí este hueco se llena con gas o aire comprimido).
cs es la capacidad del espécimen.
co es la capacitancia debido al espacio entre el electrodo y la muestra.
c es la combinación efectiva de cs y co.
De la figura de arriba, como dos condensadores están conectados en serie,
εo es la permitividad del espacio libre,r es la permitividad relativa, cuando quitamos el espécimen y el espaciado reajustado para tener el mismo valor de capacitancia, la expresión para la capacitancia se reduce a
Al equiparar (1) y (2), obtendremos la expresión final der como:
