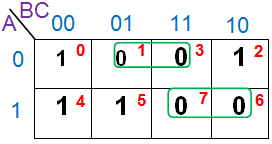
Solución de Minterm del Mapa K
A continuación se indican los pasos para obtener una solución simplificada de la minoría utilizando K-map.
Paso 1: Iniciar
Expresar la expresión dada en su forma canónica
Paso 2: Poblar el mapa K
Introduzca el valor de uno para cada término de producto en la celda del mapa K, mientras llena otras con ceros.
Paso 3: Formar grupos
- Considere los consecutivos en las celdas del mapa K y agrúpelos (recuadros verdes).
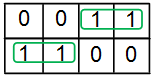

- Cada grupo debe contener el mayor número de unos y ninguna celda en blanco.


- El número de unos en un grupo debe ser una potencia de 2, es decir, un grupo puede contener


- El agrupamiento debe llevarse a cabo en orden decreciente, es decir, hay que tratar de agrupar por 8 (octetos) primero, luego por 4 (cuádruples), seguido por 2 y por último por 1 (aislados).


- La agrupación se hace ya sea horizontal o verticalmente, o en el interior de cuadrados o rectángulos. La agrupación diagonal de unos no está permitida.


- El mismo elemento o elementos pueden repetirse en múltiples grupos sólo si esto aumenta el tamaño del grupo.


- Los elementos que rodean los bordes de la mesa se consideran adyacentes y pueden agruparse.
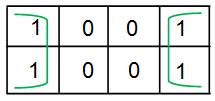

- Las condiciones de no cuidado deben considerarse sólo si ayudan a aumentar el tamaño del grupo (de lo contrario, se descuidan).
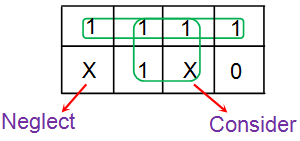

Paso 4: Obtener la expresión booleana para cada grupo
Exprese cada grupo interms de variables de entrada observando las variables comunes que se ven en el etiquetado de las células. Por ejemplo, en la figura que se muestra a continuación hay dos grupos con dos y un número de uno en ellos (Grupo 1 y Grupo 2, respectivamente). Todos los del Grupo 1 de la K-map están presentes en la fila para la cual A = 0. Por lo tanto, contienen la variable A. Además, estas dos están presentes en columnas adyacentes que sólo tienen en común el término B, como se indica en la flecha rosa de la figura.
Por lo tanto, el siguiente término es B. Esto da el término de producto correspondiente a este grupo como AB. De manera similar, el del Grupo 2 del mapa K está presente en la fila para la cual A = 1. Además las variables correspondientes a su columna son BC. Así se obtiene el término de producto global para este grupo como ABC.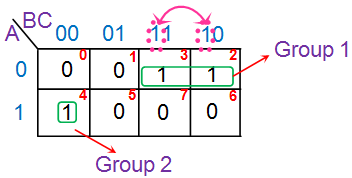

Paso 5: Obtener la expresión booleana para la salida
Los términos del producto obtenidos para grupos individuales se combinarán para formar una forma de suma de productos (SOP) que produzca el total de la expresión booleana simplificada. Esto significa que para el mapa K que se muestra en el paso 4, la expresión de salida simplificada general es
A continuación se muestran algunos ejemplos más en los que se elabora el proceso de simplificación del mapa K.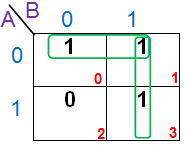

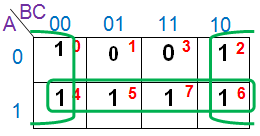

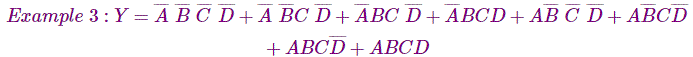
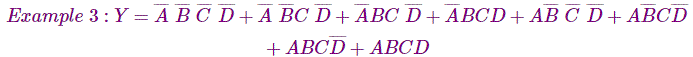
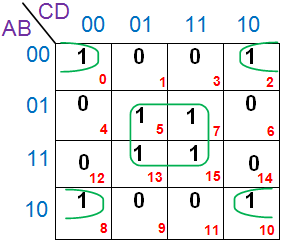

Solución Maxterm del Mapa K
El método que se debe seguir para obtener una solución de maxterm El uso de K-map es similar al de solución de minterm excepto los cambios menores que se enumeran a continuación.
- K-map las células deben ser pobladas por ceros para cada término de suma de la expresión en lugar de unos.
- La agrupación debe ser llevada a cabo por ceros y no por unos.
- Expresiones booleanas para cada grupo deben expresarse como términos de suma y no como términos de producto.
- Las sumas de todos los grupos individuales deben combinarse para obtener la expresión booleana simplificada general en forma de producto de suma (POS).