La simplificación de las expresiones booleanas es un paso importante en el diseño de cualquier sistema digital. Mapas de Karnaugh o K-maps es una de esas técnicas de simplificación, introducida por Maurice Karnaugh en 1953, que es de naturaleza gráfica. Este método de minimizar las expresiones lógicas es más adecuado cuando el número de variables involucradas es menor o igual a cuatro. Esto se debe a que K-map emplea el uso de tablas bidimensionales para simplificar las expresiones, cuyo tamaño aumenta a un ritmo muy elevado con el aumento del número de variables. Este hecho se establece además en la figura 1, que muestra los mapas K para dos, tres y cuatro variables en orden.
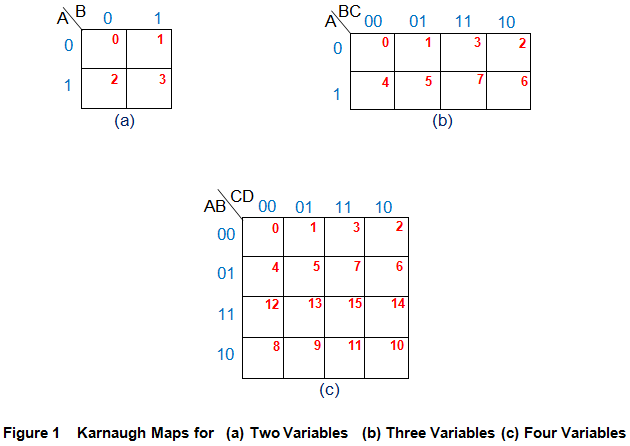

A partir de la cifra, es evidente que el número de celdas del mapa K es una función del número de entradas. En general, si hay n entradas, entonces el mapa K correspondiente tiene que ser de 2n células. Por ejemplo, si el número de variables de entrada es 2, entonces tenemos que considerar un mapa K con 4 (=22), mientras que si hay 3 variables de entrada, entonces requerimos un 8 (=23) de la celda K-map, y de forma similar para 4 entradas se obtiene 16 (=24) célula K-map y así sucesivamente.
Estructura del K-map
Se considera que todos los mapas K, independientemente de su tamaño, poseen una estructura generalizada (Figura 1). Cada mapa K tiene un conjunto de variables de entrada representadas en su esquina superior izquierda (alfabetos negros). Estas son las variables de entrada que intervienen en la expresión lógica que debe simplificarse. El valor o valores de estas variables se muestran en binario a lo largo de sus respectivos lados (combinación de ceros y unos en azul). Aquí se ve que los patrones binarios de dos celdas adyacentes cualesquiera difieren en un solo bit. Este tipo de esquema de codificación se denomina código gris y se emplea para facilitar el proceso de agrupación que a su vez minimiza la expresión lógica.
Además, se observa que estas secuencias binarias asignan un patrón de bits de entrada definido para cada celda del mapa K, cuyo equivalente decimal se muestra en números rojos dentro de cada una de ellas. Por ejemplo, la tercera celda de la primera fila de la figura 1b corresponde al patrón de bits de entrada ABC = 011 que se representa por su equivalente decimal 3.
El procedimiento de simplificación del mapa K se inicia introduciendo los valores de la variable de salida (ya sea para la suma de productos, SOP o para el producto de suma, POS) en las celdas apropiadas del mapa K. Luego hay que agrupar el número máximo de unos (en el caso de SOP) o ceros (en el caso de POS). Estos grupos deben ser necesariamente en potencias de 2 y deben ser llevados en orden descendente solamente. Por ejemplo, si hay 8 celdas en el mapa K, entonces, primero, trate de agrupar para 8 (=23), luego por 4 (=22), siguiente para 2 (=21) y, por último, considerar los términos aislados. Después de esto, cada grupo se expresa interms de la combinación de variables de entrada que corresponden a los valores binarios comunes a lo largo de las filas y columnas asociadas. Finalmente, estos se utilizan para expresar la salida de la expresión lógica.
Ventajas del Mapa de Karnaugh
Las ventajas del K-map se muestran a continuación
- La simplificación del mapa K no exige el conocimiento de Los teoremas algebraicos de Boole.
- Por lo general, requiere un menor número de pasos en comparación con la técnica de minimización algebraica.
Desventajas del mapa de Karnaugh
Las desventajas del K-map se muestran a continuación
- La complejidad de K-map El proceso de simplificación aumenta con el incremento del número de variables
- La expresión mínima obtenida podría no ser única