Introducción del sistema numérico binario
En electrónica digital Los números binarios son la herramienta más importante para dar entradas digitales. Ahora, antes de entender sistema numérico binariotenemos que entender el sistema de números decimales, que usamos en nuestra vida diaria. El sistema numérico introducido por primera vez en la historia de la humanidad con el propósito de contar. Los diferentes números para contar están representados por diferentes símbolos. Así como una sola cosa se cuenta por un símbolo 1, si hay dos cosas, el símbolo será 2, para contar tres cosas, el símbolo es 3. Para cuatro, cinco, seis, siete, ocho, nueve los símbolos utilizados en los sistemas decimales son 4, 5, 6, 7, 8 y 9 respectivamente. El símbolo 0 (cero) significa que no hay nada que contar. Así, 0 ,1, 2, 3, 4, 5, 6, 7, 8, 9 son diez símbolos básicos usados para contar de cero a nueve. Por eso se llama sistema numérico decimal o sistema de base 10.
Pero si hay más de nueve cosas que contar, entonces no vamos por otro símbolo nuevo, sino que combinamos dos o más símbolos del 0 al 9 y representamos los números que son más de nueve. Para representar nueve + uno que es diez, usamos 10, para nueve + dos usamos 11 y así sucesivamente. De esta manera establecimos el sistema numérico decimal.
Ahora llegando al sistema numérico binario, el nombre es así porque tiene dos bases (0 y 1), todo el sistema de no. puede ser representado por él.
Historia del sistema numérico binario
Sistema numérico binario fue introducida por un erudito indio, Pingala, alrededor de los siglos V y II a.C. Las sílabas largas y cortas fueron usadas por él para ilustrar los dos tipos de números, es más como el código Morse.
Gottfried Leibniz en 1679 introdujo el tipo moderno de sistema de números binarios que todavía usamos.
Cualquier tipo de número (decimal) puede ser representado por el sistema numérico binario. El uso de este sistema es popular en la electrónica digital porque el modo de encendido y apagado puede ser muy fácil de entender por esto.
Aquí, en la tabla anterior, cada número está representado por la combinación de dos de los símbolos básicos (0 a 9). Estos símbolos básicos se conocen como dígitos y la posición correspondiente de estos dígitos en un número representado se conoce como bit. Así que todos los números decimales representados arriba son dos dígitos, número de bits dobles. El bit más a la izquierda de un número se denomina bit más significativo (MSB), mientras que el bit más a la derecha se denomina bit menos significativo (LSB).
Si observamos los números dados arriba encontraremos que los primeros diez números sucesivos, es decir, del 00 al 09, están representados por el cambio de diez dígitos decimales en LSB. Entonces MSB se cambia al siguiente dígito sucesivo y al cambiar los dígitos en LSB se representan otros diez números sucesivos (del 10 al 19). En la tercera fila de la tabla se cambia el MSB al siguiente dígito sucesivo y al cambiar los dígitos en LSB se representan otros diez números sucesivos (del 20 al 29). Hay un total de 100, es decir, de 00 a 99 números representados por dos bits en el sistema decimal. 100 significa 102 lo que implica (número de dígitos básicos)número de bits. Por lo tanto, por 3 bits 103 o 1000 números (es decir, de 000 a 999) pueden ser representados. De manera similar, por n bits 10n los números pueden ser representados.
Ahora piense en la situación, donde un sistema numérico tiene sólo dos dígitos 0 y 1. Este sistema también puede ser representado en la misma lógica que el sistema decimal. El sistema numérico con sólo dos dígitos 0 y 1 se conoce como sistema numérico binario. Aquí, el cero se representa con un símbolo 0 y el uno se representa como 1, pero si el número es más de uno, entonces el MSB se cambia a 1, y al cambiar el LSB se pueden representar otros dos números sucesivos. Al igual que el sistema decimal, los números totales contados por sistema binario depende de sus bits. Para dos bits binarios, 22 los números, es decir, de cero a tres pueden ser representados. La fórmula es la misma aquí, los números totales representados por el sistema numérico binario = (número de dígitos básicos)número de bits. Número de dígitos básicos en sistema binario es dos (0 y 1) pero el número de bits puede ser elegido cualquier cosa desde el 1 hasta el infinito, por lo tanto todo el rango de números puede ser fácilmente representado por el sistema binario, como todo otro sistema numérico.
Definición del sistema numérico binario
El sistema numérico binario tiene la base (o radix) 2 y los números de este sistema están formados por dos dígitos 1 y 0.
Ahora, piensa en un número decimal como el 625. A partir de un concepto muy básico podemos entender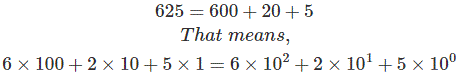
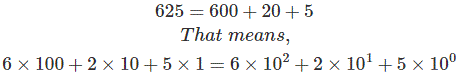
Aquí, 625 es un número decimal de tres bits, cuyo dígito más derecho o dígito en LSB es 5 y si contamos los bits de la derecha el más bit será 0. El siguiente bit de la derecha se numera como 1 y aquí se coloca el dígito 2 y de manera similar el más bit de la izquierda es 2 y el dígito es 6. Así que a partir de este ejemplo está claro que cualquier número decimal puede ser representado como
dígito 10posición o bit correspondiente
Aquí en la expresión anterior 10 es el número total de dígitos utilizados en el sistema decimal, es decir, de 0 a 9
Como el sistema decimal, cualquier sistema numérico puede ser representado por la misma expresión, sólo 10 en la expresión debe ser reemplazado por el número total de dígitos utilizados en ese sistema. Por lo tanto, cualquier número en cualquier sistema, puede ser representado como
dígito (número de dígitos utilizados en ese sistema)posición o bit correspondiente
El número de dígitos utilizados en el sistema numérico binario es 2. Por lo tanto, cualquier número puede ser representado en este sistema por,
dígito (2)posición o bit correspondiente
| 5 | 4 | 3 | 2 | 1 | 0 | → Posición o bit |
| 1 | 0 | 1 | 0 | 1 | 0 | → Los dígitos binarios |
Aquí, el número binario número 101010. Por lo tanto, según la expresión anterior, el número puede expresarse como,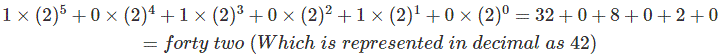
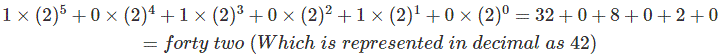
Para una mejor comprensión, por favor, observe la siguiente tabla,
| Número binario | Equivalente decimal | |||||||
| Posición o morder… |
7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 027 + 026 + 025 + 024 + 023 + 022 + 021 + 020 = 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 027 + 026 + 025 + 024 + 023 + 022 + 021 + 1×20 = 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 027 + 026 + 025 + 024 + 023 + 022 + 1×21 + 020 = 2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 027 + 026 + 025 + 024 + 023 + 022 + 1×21 + 1×20 = 3 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 027 + 026 + 025 + 024 + 023 + 1×22 + 021 + 020 = 4 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 027 + 026 + 025 + 024 + 023 + 1×22 + 021 + 1×20 = 5 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 027 + 026 + 025 + 024 + 023 + 1×22 + 1×21 + 020 = 6 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 027 + 026 + 025 + 024 + 023 + 1×22 + 1×21 + 1×20 = 7 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 027 + 026 + 025 + 024 + 1×23 + 022 + 021 + 020 = 8 |
Vea el golpe de animación para tener una idea de cuán diferente números binarios contado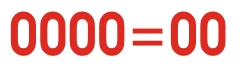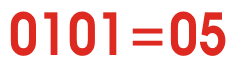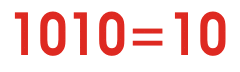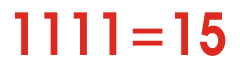
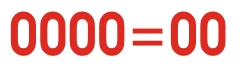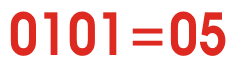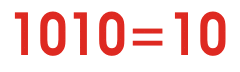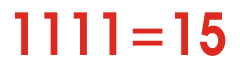
Conversión de decimal a binario
Esto es muy simple, se puede entender claramente si seguimos el ejemplo. Dejemos que un número decimal sea (87)10. Dividimos 87 por 2 y obtenemos 43 como el cociente y 1 como el resto. Estos restos se escriben al lado como se muestra a continuación.
| 2 | 87 | → 1 |
| 2 | 43 | → 1 |
| 2 | 21 | → 1 |
| 2 | 10 | 0 |
| 2 | 5 | → 1 |
| 2 | 2 | 0 |
| 1 |
La posibilidad de remanente (87)10 = (1010111)2 es sólo 1 y 0. Por lo tanto, el número se cuenta desde el último resto. Como el 1 → 0 → 1 → 0 → 1 → 1 → 1. Así es como conversión de decimal a binario está hecho.
Conversión binaria a decimal
Esta conversión también es un método muy simple. Dejemos que un número binario sea (11010)2 Donde el peso de los dígitos binarios del M.S.B. son 2…4, 23, 22, 21, 20 respectivamente. Ahora los bits se multiplican con sus pesos y la suma de esos productos es el número de decimeles respectivo. Ahora sigamos los siguientes pasos matemáticamente.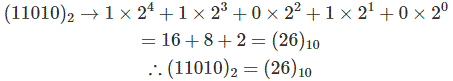
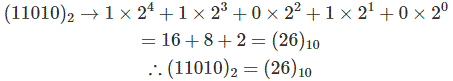
Por lo tanto, (26)10 es el número decimal requerido. Así es como conversión binaria a decimal está hecho