En los primeros días sistema de número octal se utilizaba principalmente en minicomputadoras. La palabra TCO significa ocho. El sistema de número octal dice que es un sistema numérico de base 8, lo que significa que necesitamos 8 símbolos diferentes para representar cualquier número en el sistema octal. Los símbolos son 0, 1, 2, 3, 4, 5, 6 y 7. El número más pequeño de dos dígitos en este sistema es (10)8 que equivale al decimal 8.
Por ejemplo, en este sistema de números, el número se escribe como (352)8. La base debe escribirse como 8, de lo contrario se supone que el número está en el sistema numérico decimal por defecto. Por lo tanto, esto debe ser tenido en cuenta al escribir el número. Un pequeño error puede resultar en el cambio de la base del sistema numérico. La principal ventaja de usar el sistema numérico octal es que puede ser convertido directamente a binario de una manera muy fácil. Como sabemos, el ordenador sólo entiende el sistema numérico binarioasí que la conversión de binario a octal o de octal a binario es bastante más fácil, por lo que se utiliza este sistema numérico.
Como su base es 8 = 23cada símbolo de este sistema puede ser representado por su equivalente binario de tres bits.

Como cada dígito de un número en el sistema octal se representa por separado por su equivalente binario de tres bits, el sistema octal requiere un tercio de la longitud en comparación con los números binarios. Es básicamente un sistema numérico ponderado posicionalmente. Las posiciones de los dígitos en el sistema numérico octal tienen peso como![]()
![]()
Conversión de números
Conversión de octal a binario
La conversión se realiza convirtiendo un dígito octal individual a binario. Cada dígito debe ser convertido a un número binario de 3 bits y el resultante será el equivalente binario de un número octal.
Ejemplo
Conversión (145.56)8 a binario…

Esta tabla debe utilizarse para convertir cualquier número octal en binario. De la tabla, escribiendo el equivalente binario de cada uno de los dígitos que obtenemos-
que es el equivalente binario del número octal.
Conversión binaria a octal
La misma tabla puede utilizarse para convertir un número binario en octal. Primero, agrupa el número binario en el grupo de tres bits y escribe el equivalente octal del mismo.
Ejemplo
Equivalente octal de (11001111)2 es
Los grupos que tenemos aquí son…
011,001,111. Un cero antes del número se añade para completar la agrupación en forma de tres dígitos binarios.
Ahora el equivalente octal de los números son…
3, 1, 7. Así que el número octal que tenemos es (317)8.
Conversión de octal a decimal
El método de convertir un número octal en su equivalente decimal es muy simple. Sólo hay que expandir el número en la base del ocho con su peso posicional y la resultante será un número decimal.
Ejemplo
Conversión (317)8 a su equivalente decimal.
Esto puede hacerse de la siguiente manera…
Conversión de decimal a octal
Esto puede hacerse dividiendo el número por 8 utilizando el método de división repetida conocido como método de doble salto. Se hace la división repetida y se toma el resto. Se puede hacer de la siguiente manera.
Ejemplo
Encuentra el equivalente octal de 158.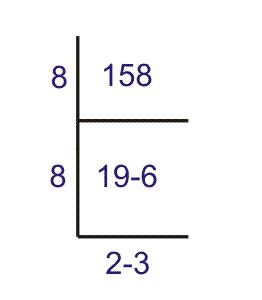

El número equivalente en el sistema octal es (236)8.
Cuando hay un número en fracción o después del punto decimal, que se puede convertir en-
Digamos que tenemos que convertir 0,40 a octal.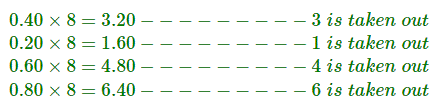

Así que vemos que el número se repite. Esto continuará y será un proceso interminable para que podamos aproximar el resultado a-
(.3146…)8.
Ventajas de los sistemas de número octal
- Es de un tercio de longitud del binario.
- Fácil proceso de conversión de binario a octal y viceversa.
- Más fácil de manejar la entrada y la salida en la forma octal.
Desventajas de los sistemas de número octal
La computadora no entiende sistema de número octal por lo que debe haber un requisito de circuitos adicionales conocidos como convertidores de octal a binario antes de que se aplique a un sistema digital o a una computadora.

