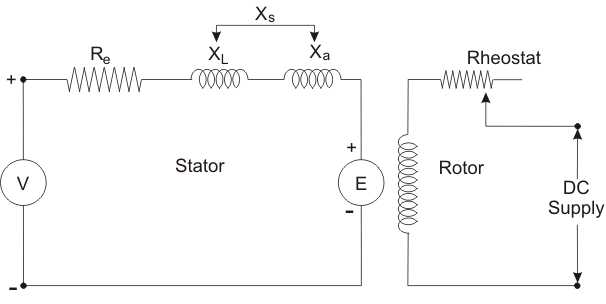

V = Voltaje de terminal
Re = Resistencia efectiva
XL = Reactancia de fuga
Xa = Reactancia ficticia
Xs = Reactancia síncrona
E = Contrapartida emf
En caso de motor sincrónico la estructura del campo giratorio debe ser energizada por corriente directa. En el devanado del estator se deben considerar dos efectos: el efecto del corte de los conductores del estator a velocidad sincrónica y el efecto del campo giratorio del estator. A voltaje inducido en el bobinado del estator debido al campo magnético rotativo. Este voltaje se llama contra-emf (E) opone el voltaje aplicado (V) al estator. La magnitud del EMF inducido depende de la fuerza de la corriente de excitación. En la sección del estator hay dos reactancias contadas, una es la reactancia de fuga y la otra es la reactancia ficticia. El efecto de la reacción de armadura puede ser sustituido por la reactancia ficticia (Xa) que cuando se combina con la reactancia de fuga de la armadura da una reactancia sincrónica (Xs) combinado con la resistencia efectiva de la armadura (Re) da la impedancia sincrónica (Zs).
Método de Factor de Potencia Cero o Triángulo de Potier
Antes de discutir el triángulo de Potier tenemos que discutir la característica de Potier. La característica de factor de potencia cero (ZPFC) de un alternador es una curva de la tensión terminal del inducido por fase trazada contra la corriente de campo con una corriente de inducido nominal constante a velocidad síncrona y un f.p. de retardo cero. La forma del gráfico característico del factor de potencia cero es muy parecida a la del O.C.C. desplazado horizontalmente hacia abajo.
El diagrama de los fáseres como sigue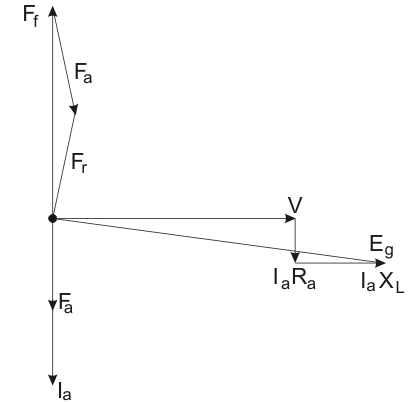

Aquí,
Y = Voltaje de terminal
Ia = Corriente de armadura
Ra = Resistencia de la armadura
XL = Reactancia de fuga
Eg = Voltaje generado por fase
Fa = Reacción de la armadura mmf
Ff = Campo mmf
Fr = Emf resultante
Si descuidamos la resistencia de la armadura, el fásor hará lo siguiente…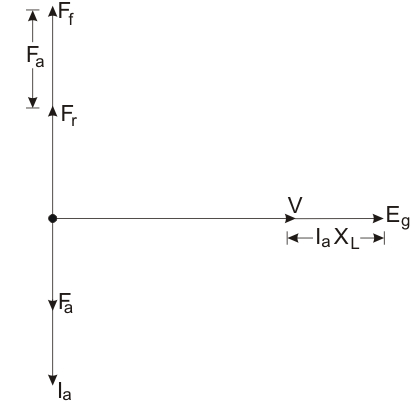

Tomando el voltaje terminal de referencia a cero f.p. de retraso, la corriente de armadura se retrasa voltaje por 90o. Aquí.aRa paralelo a la I.a, IaXL perpendicular a Ia.
Entonces podemos decir que desde el primer diagrama de fases
Del segundo diagrama de fases podemos decir que el voltaje terminal (V), la caída de voltaje de la reactancia (IaXL), y el voltaje generado (Eg) están en fase.
Aritméticamente decimos que..:
También los fáseres de tres mmf están en fase para que podamos decir que..:
Si convertimos esta ecuación en la corriente de campo equivalente dividiendo sus dos lados por Tf que es el número efectivo de vueltas por polo en el campo de roter.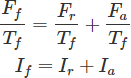
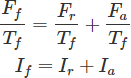
Dónde,
If = Corriente de campo
Ir = Corriente resultante
Ia = Corriente de armadura
Consideremos b a cero p.f. tallar a la tensión nominal de los terminales (v) y a la corriente de campo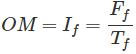
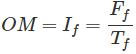
La corriente de armadura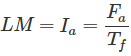
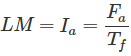
La corriente resultante![]()
![]()
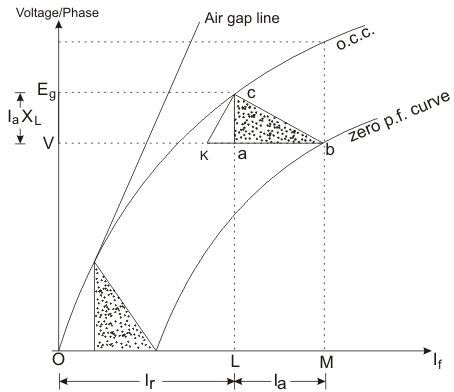

El actual campo OL resultaría en la generación de
De modo que la distancia vertical AC debe ser igual a la caída de voltaje de la reactancia de fuga (IaXL)![]()
![]()
El triángulo formado por los vértices a, b, c llamado Triángulo de Potier.



