Motor Schrage es esencialmente una combinación de motor de inducción de rotor bobinado y convertidor de frecuencia. El motor Schrage puede ser tratado como un motor de inducción polifásico invertido. A diferencia de motor de inducción el bobinado primario del motor Schrage está en el rotor. El suministro trifásico se da al primario con la ayuda de 3 anillos colectores. El devanado secundario está en el estator. Aparte del primario y el secundario hay un tercer tipo de bobinado llamado terciario que está conectado al conmutador. El primario y el terciario están alojados en las mismas ranuras del rotor y están acoplados mutuamente. Los terminales del devanado secundario están conectados al conmutador por medio de tres juegos de cepillos móviles A1A2, B1B2 y C1C2. La posición del cepillo puede ser cambiada por una rueda proporcionada en la parte trasera del motor. El desplazamiento angular entre los cepillos determina el EMF inyectado en el devanado secundario que se requiere para el control de la velocidad y el factor de potencia.
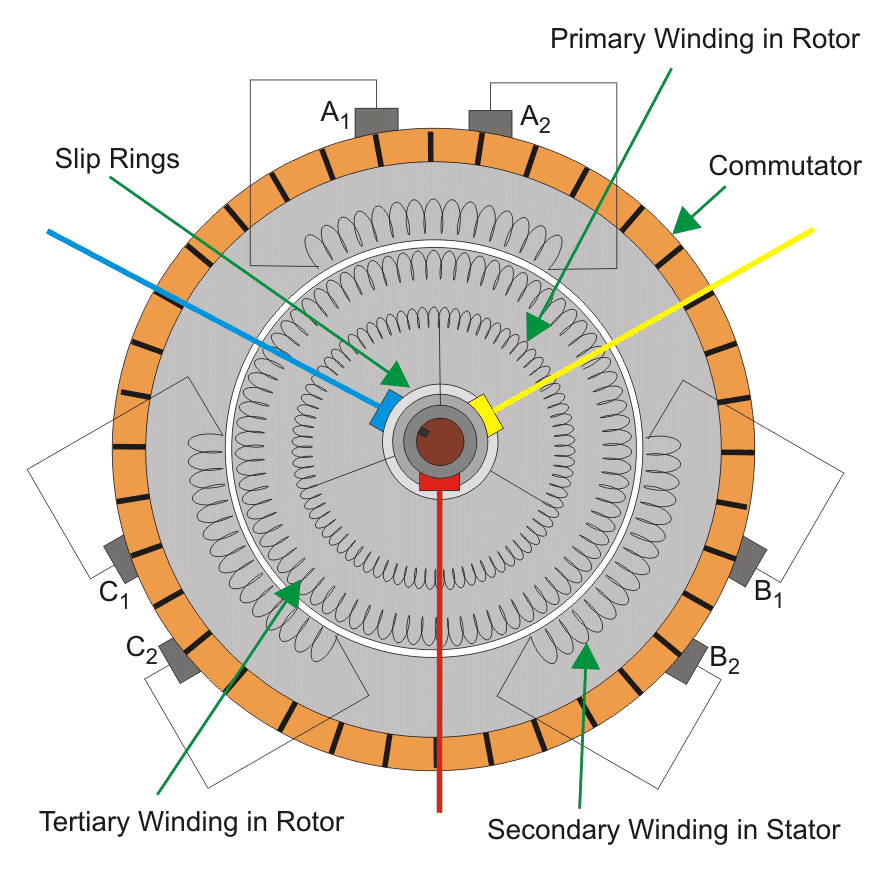

Principio de funcionamiento del motor Schrage
En condiciones de reposo debido a las corrientes trifásicas que fluyen en el devanado primario se produce un campo giratorio. Este campo giratorio corta al secundario con una velocidad sincrónica ns.
Por lo tanto, de acuerdo con La ley de Lenzs el rotor girará en una dirección para oponerse a la causa, es decir, para inducir la frecuencia de deslizamiento emfs en el secundario. Por lo tanto, el rotor gira en sentido contrario a la dirección de rotación del campo de rotación sincrónica. Ahora el campo de entrehierro está rotando a una velocidad de deslizamiento ns nr con respecto a la secundaria. Por lo tanto, la EMF recogida por los cepillos estacionarios está en la frecuencia de deslizamiento y por lo tanto es adecuada para la inyección en el secundario.
Control de velocidad del motor Schrage
Control de la velocidad del motor schrage es posible variando la EMF inyectada en el motor que puede ser controlada cambiando el desplazamiento angular entre los dos cepillos. Para entender el control de la velocidad del motor schrage entendamos el control de la velocidad en WRIMs usando el método de emf inyectado.
Considere los siguientes circuitos del rotor (los valores son sólo para fines ilustrativos).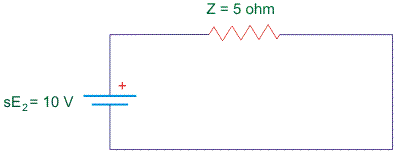

Dejemos que el par eléctrico inicial (Te) = par de carga (Tl) = 2Nm
Corriente del rotor Ir = 2A.
Vamos a ver…2 = deslizamiento emf inducido en el rotor ckt.
Y Ej = EMF inyectada en el rotor CKT.
Caso 1: Cuando Ej está en fase de oposición al sE2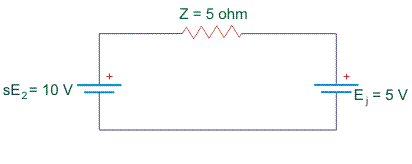

Ahora la corriente del rotor se convierte en Ir = 1A. Por lo tanto Te < Tl debido a que el motor se desacelera. Por lo tantor disminuye. Eso implica que el deslizamiento aumenta. Por lo tantor disminuye hasta el sE2 se convierte en 15V y yor = 2A, es decir, hasta Te = Tl otra vez.
Caso 2: Cuando Ej está en fase con sE2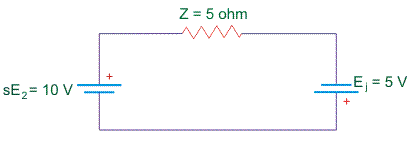

Ahora la corriente del rotor se convierte en 3A. Por lo tanto Te > Tl debido a que el motor se acelera. Por lo tantor …aumenta. Eso implica que el deslizamiento disminuye. Por lo tantor aumenta hasta el sE2 se convierte en 5V y yor = 2A, es decir, hasta Te = Tl otra vez.
Del análisis anterior se puede ver que para aumentar la velocidad el emf inyectado debe estar en fase con el emf de deslizamiento en el rotor. Para disminuir la velocidad, el EMF inyectado debe estar desfasado con el EMF de deslizamiento en el rotor.
Ahora, basándonos en los principios anteriores, echaremos un vistazo al control de la velocidad del motor de la silla.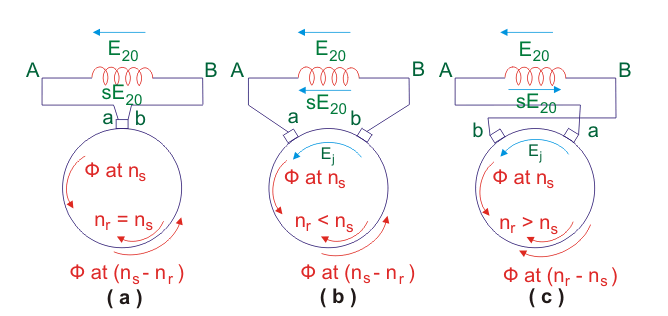

En la figura anterior
E20 = parada emf inducida en el secundario.
sE20 = inducida emf en cualquier deslizamiento s.
a, b = terminales del cepillo.
En la figura (a) ambos cepillos están conectados al mismo segmento del conmutador y por lo tanto están en cortocircuito. El EMF inyectado en este caso es cero. Por lo tanto, el rotor gira con una velocidad cercana a la velocidad sincrónica.
En la fig. b) los pinceles a y b están separados por un desplazamiento angular tal que el eje de enrollamiento terciario entre los pinceles a y b coincide con el eje de enrollamiento secundario. Ahora, al trazar el camino BAabB encontramos que la emf inyectada Ej está en fase de oposición a E20. Por lo tanto, de acuerdo con los principios antes mencionados, la velocidad del motor disminuirá de lo que era en el caso a. Por lo tanto, el motor funciona a velocidades sub-sincrónicas, es decir, nr < ns.
En la fig(c) las posiciones de los pinceles están intercambiadas. Ahora al trazar el camino BAabB encontramos que la EMF inyectada está en fase con la EMF parada E20. Por lo tanto, la velocidad del motor debe aumentar de lo que era en el caso a. Por lo tanto, el motor funciona a velocidad súper sincrónica, es decir, nr > ns.
Para cualquier separación de pinceles, la EMF inyectada está dada por![]()
![]()
De la ecuación se puede ver que el valor mínimo de emf E inyectadaj = 0 a = 0 (es decir, cuando los pinceles están en cortocircuito). Y el valor máximo de emf inyectada es Ej = Ejmax a = 90 grados (es decir, cuando los pinceles están a un polo de distancia).
Control del factor de potencia
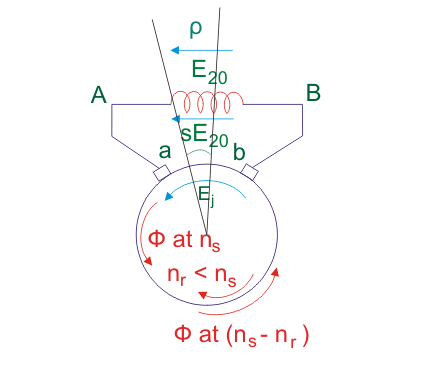

Para mejorar factor de potencia se introduce un desplazamiento angular de entre el eje de bobinado terciario y el eje de bobinado secundario. Ahora flujo corta el eje de la bobina terciaria algún tiempo después de que haya cubierto un desplazamiento angular de grados. Por lo tanto, la fase E del EMFj en este caso se retrasa el fásor E de la EMFj en el caso b por un ángulo .
El diagrama de los fáseres para los dos casos es el siguiente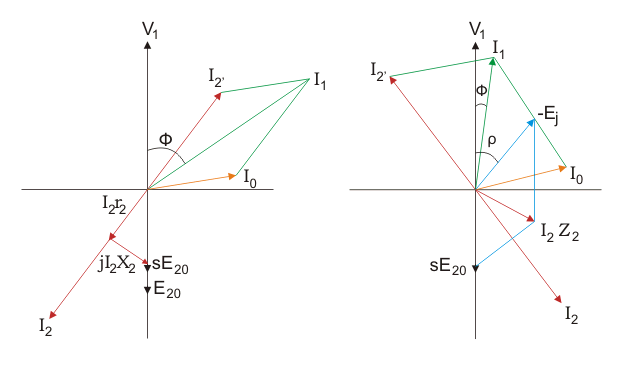

El diagrama de fases se ha construido en base a las siguientes ecuaciones:
I2 rezagos I2Z2 por algún ángulo . I2es dibujar lo opuesto a I2. El resultado de I2y la corriente magnetizadora I0 da la corriente primaria I1.
Del diagrama de fases se desprende claramente que si el eje del devanado terciario y el eje del devanado secundario se desplazan por un ángulo, el factor de potencia mejora.
Características del Schrage Motor
Si aplicamos KVL a un circuito secundario, entonces tenemos
En condiciones de no carga…2 es muy pequeño y por lo tanto puede ser descuidado.
Por lo tanto, lo hemos hecho,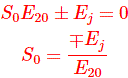
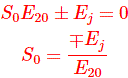
¿Dónde?0 es el deslizamiento sin carga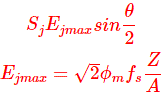
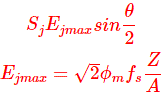
Dónde,
Ejmax es el transformador inducida por el EMF en el devanado del Terciario.
φm = vinculación de flujo máximo
fs = frecuencia de suministro
Z = número de conductores en el terciario
A = número de caminos paralelos
También
Dónde,
E20 = el transformador emf inducido en el secundario.
N2= número efectivo de vueltas en el secundario
Ahora, al sustituir estos valores en la expresión de deslizamiento sin carga, obtenemos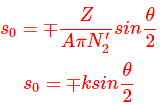
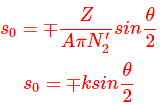
Esto implica que los valores de deslizamiento dependen completamente de las constantes de la máquina y la separación de la brocha.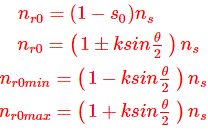
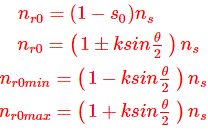
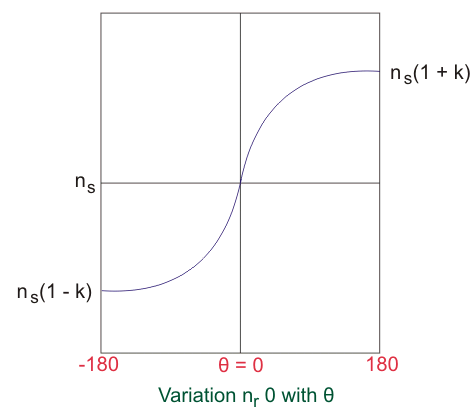

Esto demuestra que son posibles dos velocidades diferentes sin carga, dependiendo de la fase de la EMF inyectada. La magnitud de estas velocidades puede ser controlada ajustando la separación de los cepillos.
Bajo condiciones de carga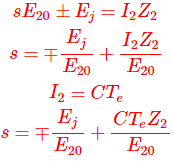
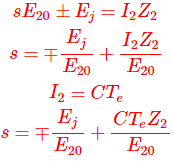
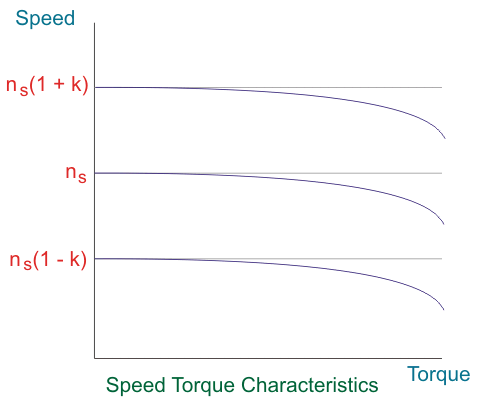

Aplicaciones
Se utiliza en accionamientos que requieren una velocidad variable como grúas, ventiladores, bombas centrífugas, transportadores, etc.


