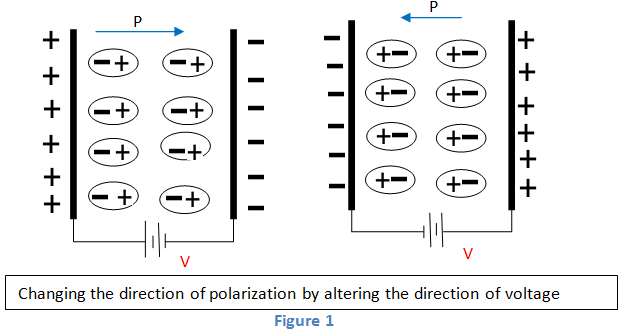
El primero que se descubrió material ferroeléctrico es la sal de Rochelle de Valasek en 1921. Estos materiales pueden producir una polarización espontánea. Invirtiendo la dirección del campo eléctrico aplicado, la dirección de la polarización de estos materiales puede ser invertida o cambiada (figura 1). Esto se llama conmutación. También puede mantener la polarización incluso una vez que se elimina el campo. Estos materiales tienen algunas similitudes sobre materiales ferromagnéticos que revelan un momento magnético permanente. El bucle de histéresis es casi igual para ambos materiales. Ya que, hay similitudes; el prefijo es el mismo para ambos materiales. Pero todo el material ferroeléctrico no debe tener Ferro (hierro). Todos los materiales ferroeléctricos exhiben un efecto piezoeléctrico. Las propiedades opuestas de estos materiales se ven en los materiales antiferromagnéticos.

Teoría de los materiales ferroeléctricos
La energía libre del material ferroeléctrico basada en la teoría de Ginburg-Landau sin campo eléctrico y cualquier estrés aplicado puede ser escrito como una expansión de Taylor. Se escribe en términos de P (parámetro de orden) como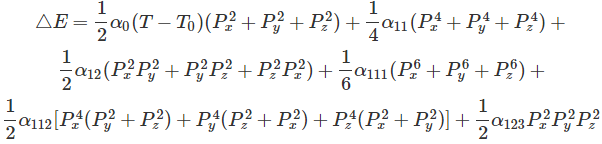
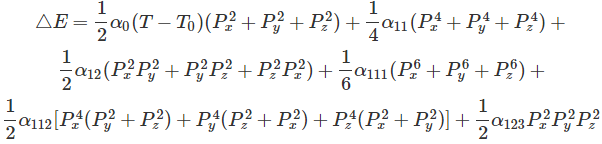
(si se utiliza la expansión de sexto orden)
Px componente del vector de polarización, x
Py componente del vector de polarización, y
Pz componente del vector de polarización, z
αi,ij,ijk Los coeficientes deben ser constantes con la simetría del cristal.
α0 > 0,111> 0 para todos los ferroeléctricos
α11< 0 ferroeléctricos con transición de primer orden
α0 > 0 ferroeléctricos con transición de segundo orden
Para investigar diferentes fenómenos y formación de dominios en los ferroeléctricos, estas ecuaciones se utilizan en el modelo de campo de fase. Normalmente se utiliza añadiendo algunos términos como un término elástico, un término de gradiente y un término electrostático a esta ecuación de energía libre. Utilizando el método de diferencias finitas, las ecuaciones se resuelven sujetas a las limitaciones de la elasticidad lineal y la ley de Gausss.
Para una transición de fase cúbica a tetragonal de una polarización espontánea de un ferroeléctrico se puede obtener de la expresión para la energía libre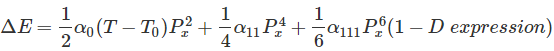
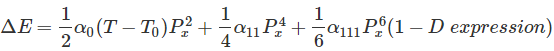
Tiene un carácter de potencial de doble pozo con mínimos de doble energía en P = Ps
Ps polarización espontánea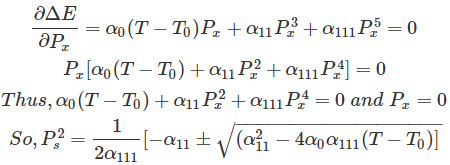
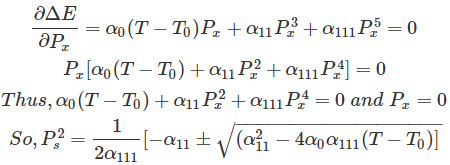
Simplificando, eliminando la raíz negativa y el sustituto11 = 0 que obtenemos,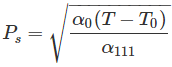
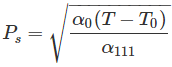
Bucle de polarización e histéresis
Primero tomamos una material dieléctrico y se da un campo eléctrico periférico, entonces podemos ver que la polarización será siempre directamente proporcional al campo aplicado que se representa en la figura 2.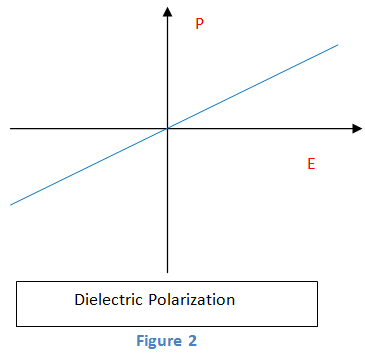

A continuación, cuando polarizamos un material paraeléctrico, obtenemos una polarización no lineal. Sin embargo, es una función del campo como se muestra en la figura 3.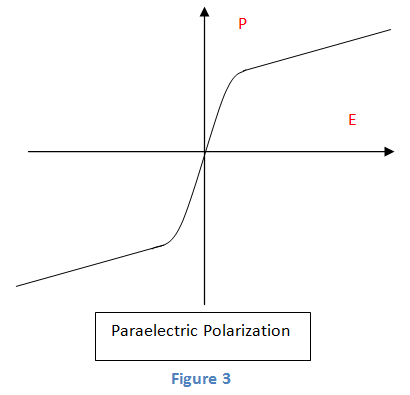

A continuación, tomamos una material ferroeléctrico y campo eléctrico se le da. Obtenemos una polarización no lineal. También muestra una polarización espontánea no nula sin un campo periférico. También podemos ver que invirtiendo la dirección del campo eléctrico aplicado, la dirección de la polarización puede ser invertida o cambiada.
Por lo tanto, podemos decir que la polarización dependerá de la condición actual y previa del campo eléctrico. El bucle de histéresis se obtiene como en la figura 4.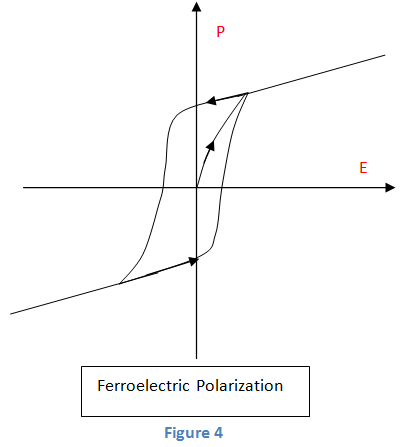

Temperatura del Curie
Las propiedades de estos materiales sólo existen por debajo de una temperatura de conversión de fase definida. Por encima de esta temperatura, el material se convertirá en material paraeléctrico. Es decir, la pérdida en la polarización espontánea. Esta temperatura definida se llama temperatura de Curie (TC). La mayoría de estos materiales por encima de Tc también perderá la propiedad piezoeléctrica. La variación de la constante dieléctrica por medio de la temperatura en el estado no polar y paraeléctrico se muestra por la ley de Curie-Weiss como se indica a continuación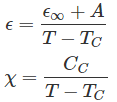
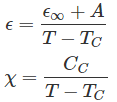
La constante dieléctrica
ε∞ a temperatura, T >> TC
Una constante
TC Punto curioso
Temperatura T
Susceptibilidad
CC La constante curiosa del material
La constante dieléctrica y la temperatura características de un material ferroeléctrico están representados a continuación.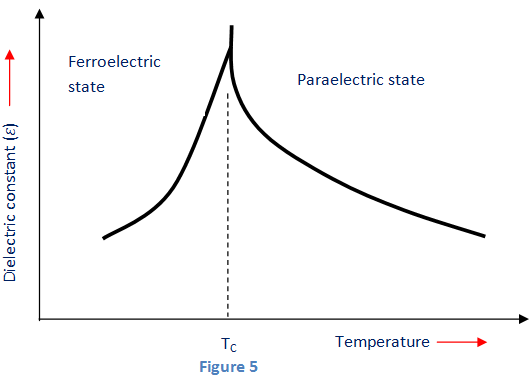

Ejemplos de materiales ferroeléctricos
- BaTiO3
- PbTiO3
- Titanato de Circonato de Plomo (PZT)
- Sulfato de triglicina
- PVDF
- Litio tantalita, etc.
Aplicación de los materiales ferroeléctricos
Los materiales ferroeléctricos tienen muchas aplicaciones, entre ellas:
- Termistores
- Osciladores
- Memoria no volátil
- Filtros
- Condensadores
- Deflectores de luz
- Transchargers
- Materiales electro-ópticos
- Moduladores
- Piezoeléctricos
- Pantalla, etc.