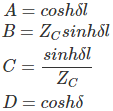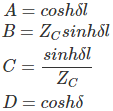¿Qué es la línea de transmisión larga?
A larga línea de transmisión se define como un línea de transmisión con una longitud efectiva de más de 250 km. A diferencia de líneas de transmisión cortas y líneas de transmisión de mediosya no es razonable asumir que los parámetros de la línea están amontonados. Para modelar con precisión una línea de transmisión larga, debemos considerar el efecto exacto de los parámetros distribuidos en toda la longitud de la línea. Aunque esto hace que el cálculo de Parámetros ABCD de la línea de transmisión más complejo, también nos permite derivar expresiones para el voltaje y la corriente en cualquier punto de la línea.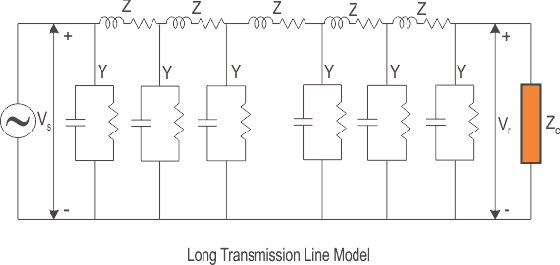

En una línea de transmisión larga, las constantes de la línea están distribuidas uniformemente en toda la longitud de la línea. Esto se debe a que la longitud efectiva del circuito es mucho mayor que la de los modelos anteriores (línea larga y media) y por lo tanto ya no podemos hacer las siguientes aproximaciones:
- Ignorando la admisión de la red, como en un modelo de línea de transmisión pequeña.
- Considerando la impedancia del circuito y admisión para ser amontonados y concentrados en un punto como fue el caso del modelo de línea media.
Más bien, por todas las razones prácticas, debemos considerar que la impedancia y la admitancia del circuito se distribuyen a lo largo de toda la longitud del circuito como se muestra en la figura siguiente. Los cálculos de los parámetros del circuito, por esta razón, van a ser ligeramente más rigurosos como veremos aquí. Para un modelado preciso para determinar los parámetros del circuito, consideremos el circuito de la larga línea de transmisión como se muestra en el siguiente diagrama.
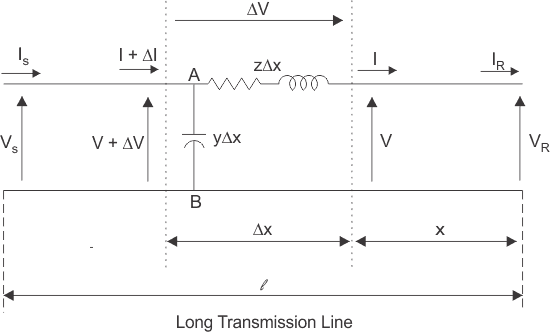

Aquí una línea de longitud l > 250km se suministra con un extremo de envío voltaje y actual de VS y yoS respectivamente, mientras que la VR y yoR son los valores de voltaje y corriente obtenidos del extremo receptor. Consideremos ahora un elemento de longitud infinitamente pequeña x a una distancia x del extremo receptor como se muestra en la figura donde.
V = valor del voltaje justo antes de entrar en el elemento x.
I = valor de la corriente justo antes de entrar en el elemento x.
V+V = voltaje que sale del elemento x.
I+I = corriente que sale del elemento x.
V = caída de voltaje a través del elemento x.
zx = impedancia en serie del elemento x
yx = admisión de la derivación del elemento x
Donde, Z = z l y Y = y l son los valores de la impedancia total y la admitancia de la larga línea de transmisión.
Por lo tanto, la caída de voltaje a través del infinitamente pequeño elemento x viene dada por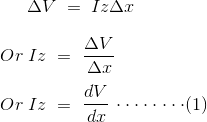
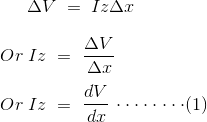
Ahora para determinar la I actual, aplicamos KCL al nodo A.
Dado que el término V yx es el producto de 2 valores infinitamente pequeños, podemos ignorarlo para facilitar el cálculo.
Por lo tanto, podemos escribir ![]()
![]()
Ahora derivando ambos lados de la ecuación (1) w.r.t x,![]()
![]()
Ahora sustituyendo ![]()
![]() de la ecuación (2)
de la ecuación (2)![]()
![]()
La solución de la anterior ecuación diferencial de segundo orden viene dada por.
Ecuación de derivación (4) w.r.to x.![]()
![]()
Ahora comparando la ecuación (1) con la ecuación (5)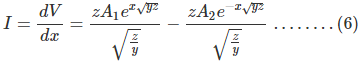
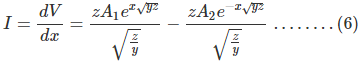
Ahora para ir más allá definamos la impedancia característica Zc y la constante de propagación de una larga línea de transmisión como![]()
![]()
Entonces la ecuación de voltaje y corriente puede expresarse en términos de impedancia característica y constante de propagación como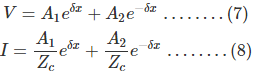
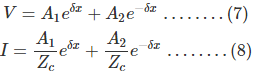
Ahora en x=0, V= VR y I= Ir. Sustituyendo estas condiciones por las ecuaciones (7) y (8) respectivamente.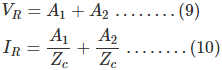
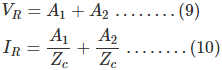
Resolviendo las ecuaciones (9) y (10),
Obtenemos valores de A1 y A2 como,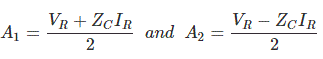
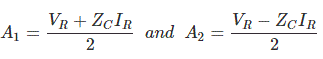
Ahora, aplicando otra condición extrema en x = l, tenemos V = VS y I = IS.
Ahora para determinar la VS y yoS sustituimos x por l y ponemos los valores de A1 y
A2 en la ecuación (7) y (8) obtenemos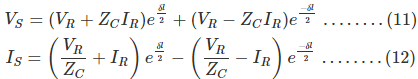
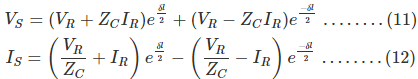
Por los operadores trigonométricos y exponenciales sabemos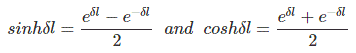
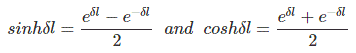
Por lo tanto, la ecuación (11) y (12) puede ser reescrita como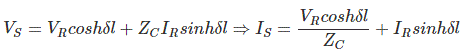
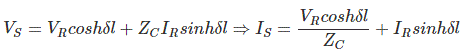
Así, comparado con la ecuación general de los parámetros del circuito, obtenemos los parámetros ABCD de un larga línea de transmisión como,