Sabemos que siempre hay un campo eléctrico estático alrededor de una carga eléctrica positiva o negativa y en ese campo eléctrico estático hay un flujo de tubo de energía o flujo. En realidad esto… flujo es irradiado/emanado por la carga eléctrica. Ahora la cantidad de este flujo de flujo depende de la cantidad de carga de la que emana. Para averiguar esta relación, el Teorema de Gauss se introdujo. Este teorema puede ser considerado como uno de los más poderosos y útiles en el campo de la ciencia eléctrica. Podemos averiguar la cantidad de flujo radiado a través de la superficie que rodea la carga de este teorema.


Este teorema establece que el total flujo eléctrico a través de cualquier superficie cerrada que rodee una carga, es igual a la carga positiva neta encerrada en esa superficie.
Supongamos que los cargos Q1, Q2_ _ _ _Qi, _ _ _ Qn están encerrados por una superficie, entonces el teorema puede ser expresado matemáticamente por la integral de la superficie como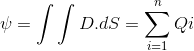
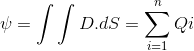
¿Dónde, D es la flujo densidad en culombios/m2 y el dS es el vector dirigido hacia el exterior.
Explicación del Teorema de Gauss
Por explicar el Teorema de Gausses mejor pasar por un ejemplo para una comprensión adecuada.
Dejemos que Q sea la carga en el centro de una esfera y el flujo emanada de la carga es normal en la superficie. Ahora, este teorema establece que el total flujo emanada de la carga será igual a los culombos Q y esto puede ser probado matemáticamente también. Pero ¿qué pasa cuando la carga no se coloca en el centro, sino en cualquier otro punto que no sea el centro (como se muestra en la figura).
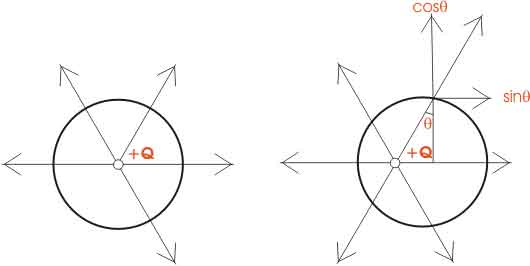

En ese momento, las líneas de flujo no son normales a la superficie que rodea la carga, entonces este flujo se resuelve en dos componentes que son perpendiculares entre sí, el horizontal es el componente sin y el vertical es el componente cos. Ahora bien, cuando la suma de estos componentes se toma para todas las cargas, entonces el resultado neto es igual a la carga total del sistema que demuestra Teorema de Gauss.
Prueba del Teorema de Gauss
Consideremos una carga puntual Q ubicada en un medio isotrópico homogéneo de permitividad.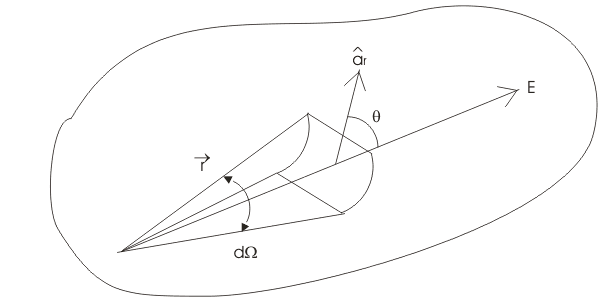

El intensidad del campo eléctrico en cualquier punto a una distancia r de la carga es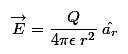
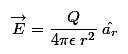
El densidad de flujo se da como,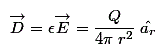
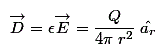
Ahora desde la figura el flujo a través del área dS

Donde, es el ángulo entre D y el normal a dS.
Ahora, dScos es la proyección de dS es normal al vector del radio. Por definición de un ángulo sólido

Donde, d es el ángulo sólido subtendido en Q por la superficie elemental son dS. Así que el desplazamiento total de flujo a través de toda la superficie es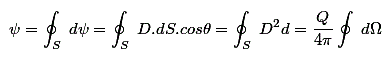
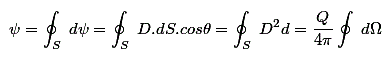
Ahora, sabemos que el ángulo sólido subtendido por cualquier superficie cerrada es de 4 estereorradiantes, por lo que el flujo eléctrico total a través de toda la superficie es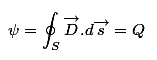
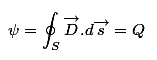
Esta es la forma integral de Teorema de Gauss. Y por lo tanto este teorema está probado.