La transformación de Laplace es una técnica para resolver ecuaciones diferenciales. Aquí la ecuación diferencial de la forma del dominio del tiempo se transforma primero en la ecuación algebraica de la forma del dominio de la frecuencia. Después de resolver la ecuación algebraica en el dominio de la frecuencia, el resultado se transforma finalmente a la forma de dominio del tiempo para lograr la solución definitiva de la ecuación diferencial. En otras palabras, se puede decir que el La transformación de Laplace no es más que un método abreviado para resolver la ecuación diferencial.
En este artículo, discutiremos Laplace se transforma y cómo se usan para resolver ecuaciones diferenciales. También proporcionan un método para formar una función de transferencia para un sistema de entrada-salida, pero esto no se discutirá aquí. Proporcionan los bloques de construcción básicos para la ingeniería de control, utilizando diagramas de bloques, etc.
Ya existen muchos tipos de transformaciones, pero Laplace se transforma y Fourier se transforma son los más conocidos. La transformación de Laplace se utiliza generalmente para simplificar una ecuación diferencial en un simple y solucionable problema de álgebra. Incluso cuando el álgebra se vuelve un poco compleja, sigue siendo más fácil de resolver que resolver una ecuación diferencial.
Mesa de transformación de Laplace
Siempre hay una tabla disponible para el ingeniero que contiene información sobre las transformaciones de Laplace. Un ejemplo de Mesa de transformación de Laplace se ha hecho abajo. Conoceremos la transformación de Laplace de varias funciones comunes a partir de la siguiente tabla.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Definición de la transformación de Laplace
Cuando se aprende la transformación de Laplace, es importante entender no sólo las tablas sino también la fórmula.
Para entender la fórmula de transformación de Laplace: Primero Sea f(t) la función de t, el tiempo para todo t 0
Entonces la transformación Laplace de f(t), F(s) puede ser definida como![]()
![]()
Siempre que la integral exista. Donde el Operador Laplace, s = + j; será real o complejo j = (-1)
Desventajas del método de transformación de Laplace
Las transformaciones de Laplace sólo pueden utilizarse para resolver complejas ecuaciones diferenciales y, como todos los grandes métodos, tiene una desventaja, que puede no parecer tan grande. Es decir, sólo se puede utilizar este método para resolver ecuaciones diferenciales CON constantes conocidas. Si tienes una ecuación sin las constantes conocidas, entonces este método es inútil y tendrás que encontrar otro método.
La historia de Laplace se transforma
La transformación en matemáticas trata de la conversión de una función en otra función que puede no estar en el mismo dominio. El método de transformación encuentra su aplicación en aquellos problemas que no pueden ser resueltos directamente. Esta transformación recibe el nombre del matemático y renombrado astrónomo Pierre Simon Laplace que vivió en Francia.
Usó una transformación similar en sus adiciones a la teoría de la probabilidad. Se hizo popular después de la Segunda Guerra Mundial. Esta transformación se hizo popular por Oliver Heaviside, un ingeniero eléctrico inglés. Otros científicos famosos como Niels Abel, Mathias Lerch y Thomas Bromwich la usaron en el siglo XIX.
La historia completa de las Transformaciones Laplace puede ser rastreada un poco más al pasado, más específicamente a 1744. Fue entonces cuando otro gran matemático llamado Leonhard Euler estaba investigando sobre otros tipos de integrales. Sin embargo, Euler no lo persiguió muy lejos y lo dejó. Un admirador de Euler llamado Joseph Lagrange; hizo algunas modificaciones al trabajo de Euler e hizo más trabajo. El trabajo de Lagrange llamó la atención de Laplaces 38 años más tarde, en 1782, donde continuó continuando donde Euler lo había dejado. Pero no fue 3 años más tarde; en 1785 donde Laplace tuvo un golpe de genio y cambió la forma de resolver las ecuaciones diferenciales para siempre. Continuó trabajando en ello y continuó desbloqueando el verdadero poder de la transformación de Laplace hasta 1809, donde comenzó a utilizar el infinito como una condición integral.
Método de transformación de Laplace
La transformación de Laplace es una parte importante de la ingeniería del sistema de control. Para estudiar o analizar un sistema de control, tenemos que llevar a cabo la transformación de Laplace de las diferentes funciones (función del tiempo). El Laplace inverso es también una herramienta esencial para averiguar la función f(t) de su forma de Laplace. Tanto las transformadas Laplace inversas como las transformadas Laplace tienen ciertas propiedades en el análisis de los sistemas de control dinámico. Las transformaciones de Laplace tienen varias propiedades para los sistemas lineales. Las diferentes propiedades son:
Linealidad, Diferenciación, integración, multiplicación, desplazamiento de frecuencia, escala de tiempo, desplazamiento de tiempo, convolución, conjugación, función periódica. Hay dos teoremas muy importantes asociados con los sistemas de control. Estos son:
- Teorema del valor inicial (IVT)
- Teorema del valor final (FVT)
La transformación de Laplace se realiza en una serie de funciones, que son impulso, impulso unitario, paso, paso unitario, paso unitario desplazado, rampa, decadencia exponencial, seno, coseno, seno hiperbólico, coseno hiperbólico, logaritmo natural, función de Bessel. Pero la mayor ventaja de aplicar la transformación de Laplace es resolver fácilmente ecuaciones diferenciales de orden superior convirtiéndolas en ecuaciones algebraicas.
Hay ciertos pasos que deben seguirse para hacer una transformación Laplace de una función de tiempo. Para transformar una función de tiempo f(t) dada en su correspondiente transformación Laplace, tenemos que seguir los siguientes pasos:
- Primero multiplica f(t) por e-sts es un número complejo (s = + j ).
- Integrar este producto con el tiempo con límites como el cero y el infinito. Esta integración da como resultado la transformación Laplace de f(t), que se denota por F(s).
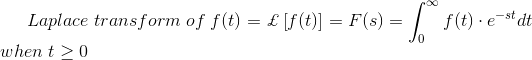
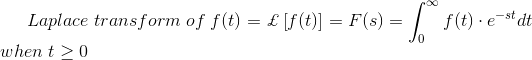
La función de tiempo f(t) se obtiene de la transformación de Laplace por un proceso llamado transformación inversa de Laplace y denotado por-1

Laplace Transformar las propiedades
Las principales propiedades de la Transformación Laplace pueden resumirse como sigue:
La linealidad: Que C1, C2 ser constantes. f(t), g(t) ser las funciones del tiempo, t, entonces

Primer Teorema del cambio:

Propiedad de cambio de escala: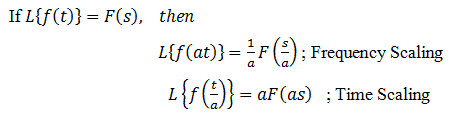
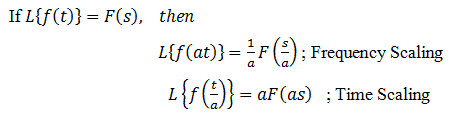
Diferenciación: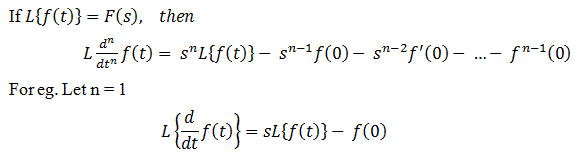
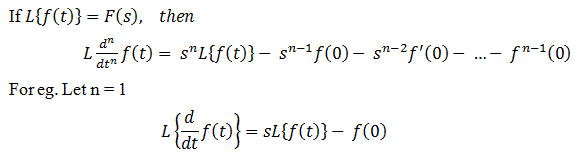
Integración: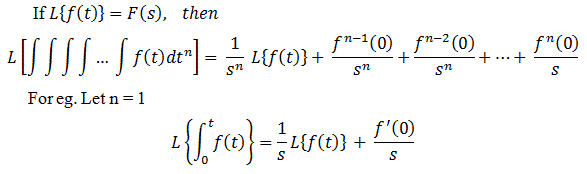
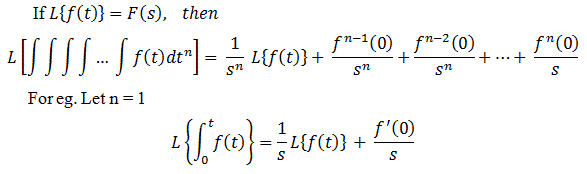
El cambio de tiempo:
Si L{f(t) } = F(s), luego la Transformada Laplace de f(t) después del retardo del tiempo, T es igual al producto de la Transformada Laplace de f(t) y e-st que es

Donde, u(t-T) denota la función de paso de unidad.
Producto:
Si L{f(t) }=F(s), entonces el producto de dos funciones, f1 t) y f)2 (t) es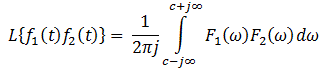
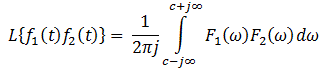
Teorema del valor final:

Este teorema es aplicable en el análisis y diseño del sistema de control de retroalimentación, ya que la Transformada Laplace da solución a las condiciones iniciales
Teorema del valor inicial:

Examinemos los métodos de transformación de Laplace de una simple función f(t) = et para entender mejor el asunto.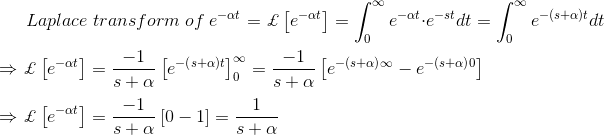
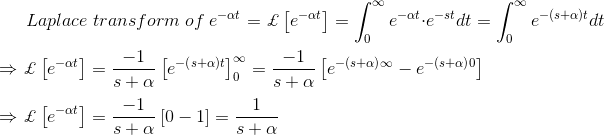
Comparando la solución anterior, podemos escribir,![]()
![]()
De manera similar, al poner = 0, obtenemos,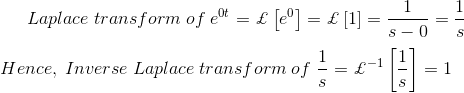
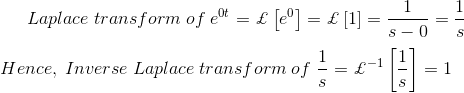
De manera similar, al poner = j, obtenemos,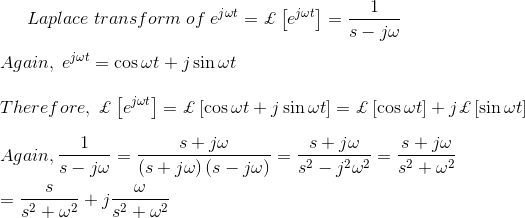
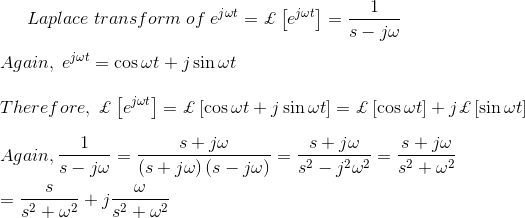
![]()
![]()
Y así,![]()
![]()
Examinemos otro ejemplo de la transformación de Laplace métodos para la función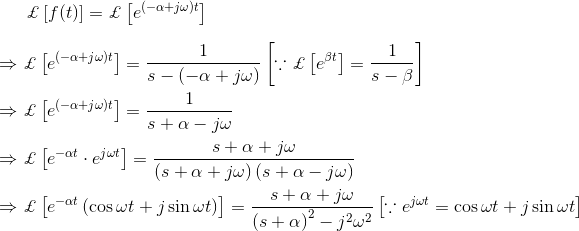
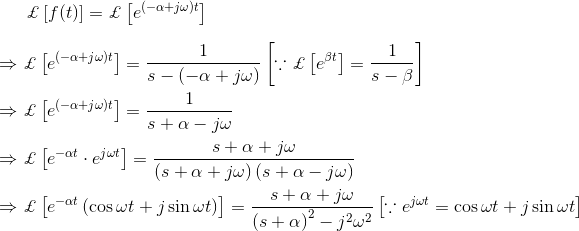
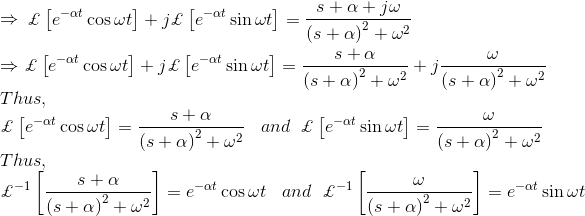
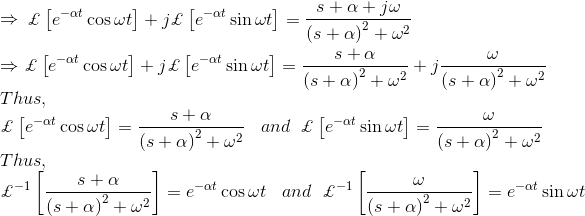
De nuevo la forma de transformación Laplace de et es,![]()
![]()
Este formulario de Laplace puede ser reescrito como![]()
![]()
Ahora, de la definición de las series de energía que obtenemos,![]()
![]()
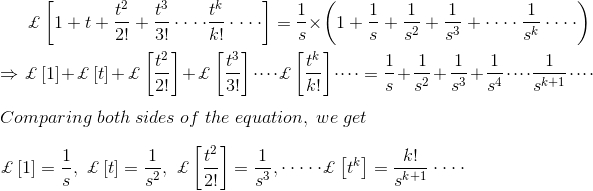
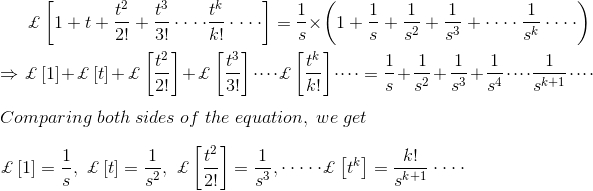
Ejemplos de transformación de Laplace
Resuelve la ecuación usando Laplace se transforma,

Usando la tabla de arriba, la ecuación puede ser convertida en forma de Laplace:

Utilizando los datos que se han dado en la pregunta se puede simplificar el formulario de Laplace.

Dividiendo por (s2 + 3s + 2) da![]()
![]()
Esto puede resolverse mediante fracciones parciales, lo que es más fácil que resolverlo en su forma anterior. En primer lugar, el denominador debe ser factorizado.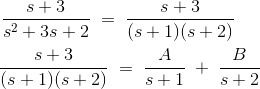
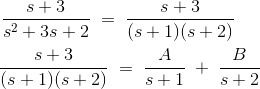
La multiplicación cruzada da:

A continuación hay que encontrar los coeficientes A y B

Sustituyendo en la ecuación:![]()
![]()
Luego, utilizando la tabla que se proporcionó anteriormente, esa ecuación puede ser convertida de nuevo a su forma normal.
Ejemplos para probarse a sí mismo
Calcule y escriba la transformación Laplace inversa de lo siguiente, se recomienda encontrar una tabla con las conversiones Laplace en línea:![]()
![]()
Soluciones: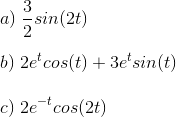
Excavemos un poco más en algunos ejemplos de transformación trabajados en laplace:
1) Donde, F(s) es la forma Laplace de una función de dominio de tiempo f(t). Encuentra la expiración de f(t).![]()
![]()
Solución![]()
![]()
Ahora, la transformación inversa Laplace de F(s), es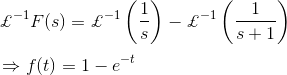
2) Encontrar la función de transformación inversa Laplace de![]()
![]()
Solución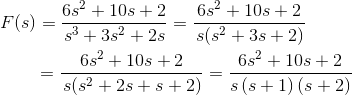
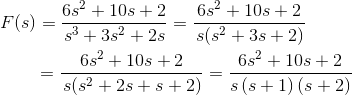
Ahora,![]()
![]()
![]()
![]()
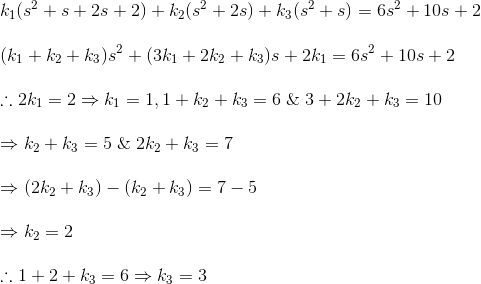
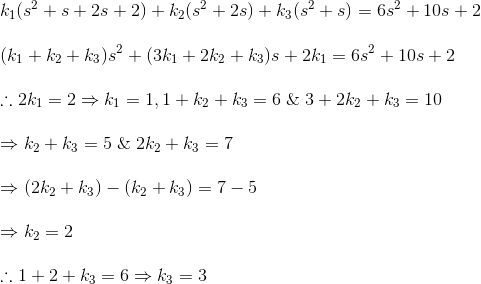
Por lo tanto,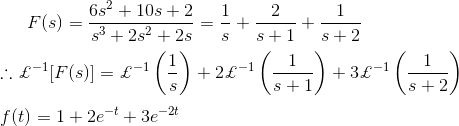
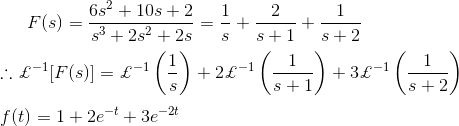
3) Resolver la ecuación diferencial![]()
![]()
Solución
Como sabemos, la transformación de Laplace de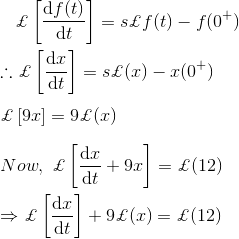
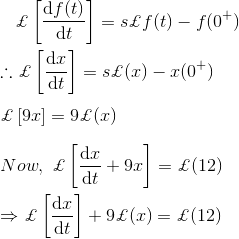
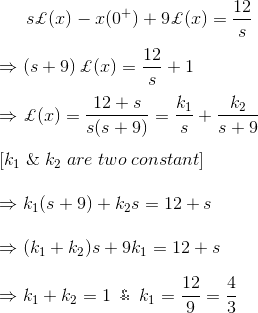
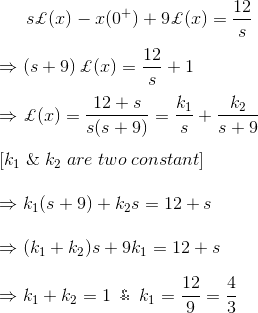
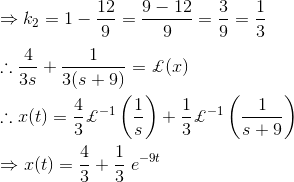
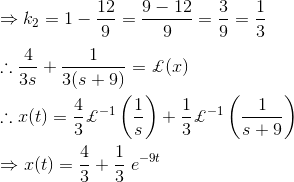
4) Resolver la ecuación diferencial,![]()
![]()
Solución
Como sabemos eso,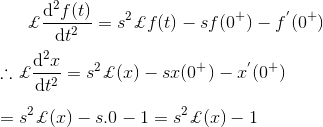
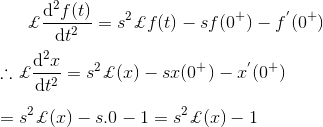
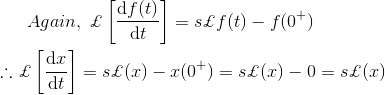
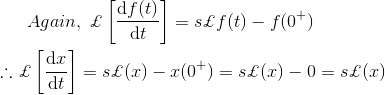
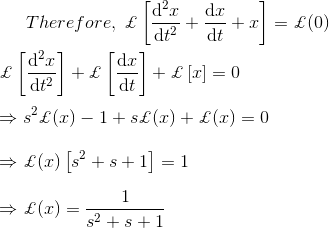
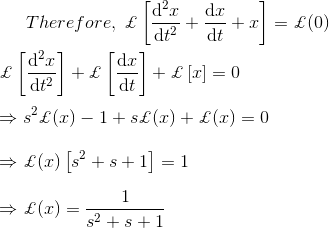
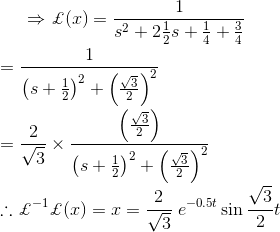
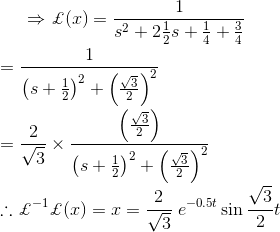
5) Para el circuito de abajo, calcule la corriente de carga inicial del condensador usando la técnica de la Transformación de Laplace.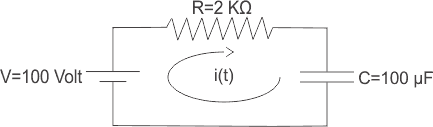

Solución
La figura anterior puede ser redibujada en forma de Laplace,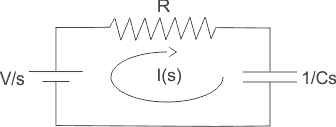

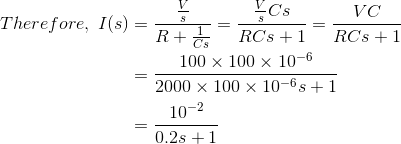
Ahora, la corriente de carga inicial,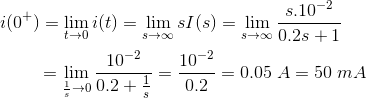
6) Resolver el El circuito eléctrico… usando la transformación de Laplace para la corriente final de estado estacionario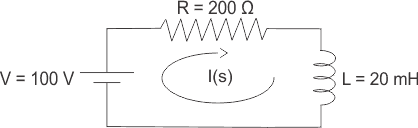

Solución
El circuito anterior puede ser analizado usando Ley de tensión de Kirchhoff y luego tenemos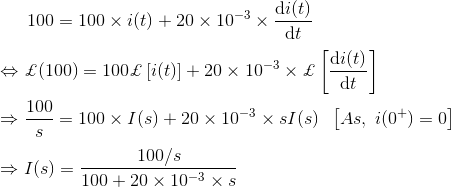
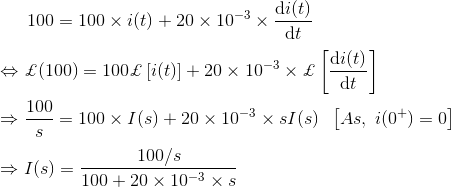
El valor final de la corriente de estado estacionario es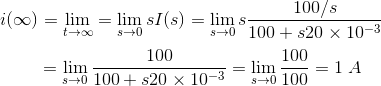
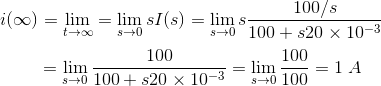
7) Un sistema está representado por la relación![]()
![]()
Donde, R(s) es la forma Laplace de la función de paso de la unidad. Encuentra el valor de x(t) en t .
Como R(s) es la forma de Laplace de la función de paso de la unidad, puede escribirse como
Solución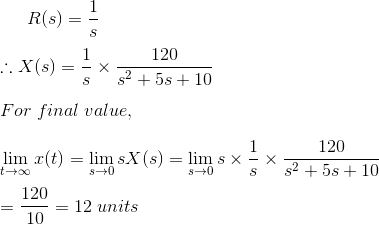
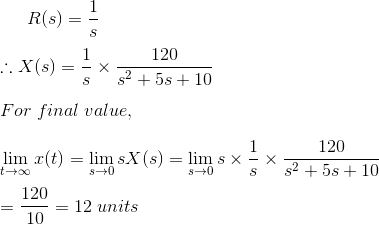
8) Encuentra f(t), f‘t) y f)“(t) para una función de dominio temporal f(t). La forma de transformación Laplace de la función se da como![]()
![]()
Aplicando el teorema del valor inicial, obtenemos,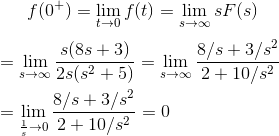
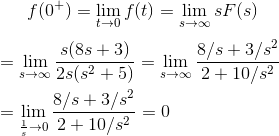
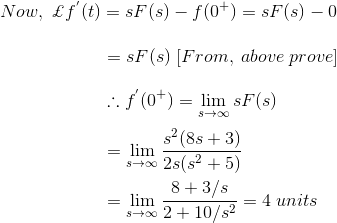
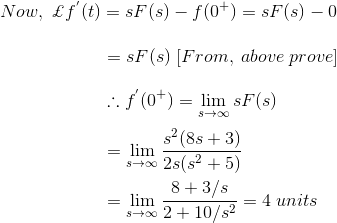
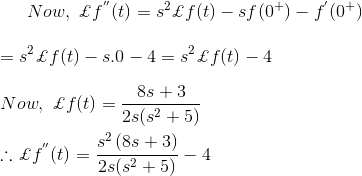
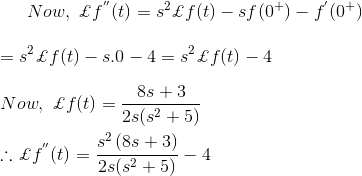
Aplicando el Teorema del Valor Inicial, obtenemos,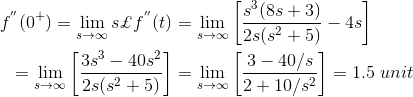
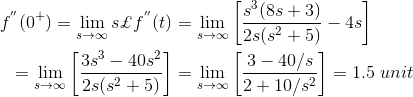
9) La Transformación Laplace de f(t) está dada por,![]()
![]()
Encuentra el valor final de la ecuación usando el teorema del valor final, así como el método convencional de encontrar el valor final.
Solución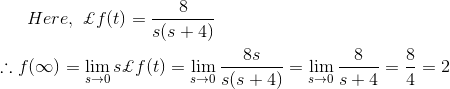
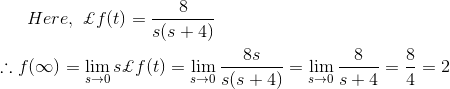
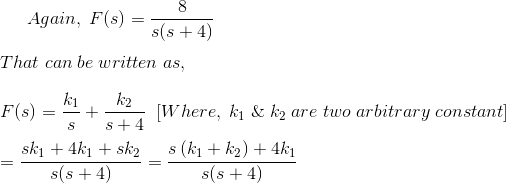
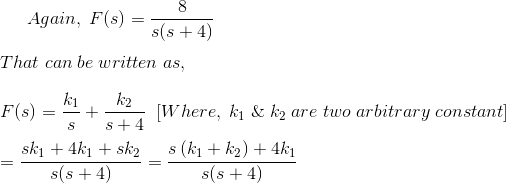
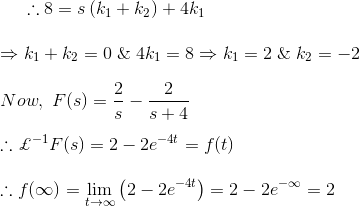
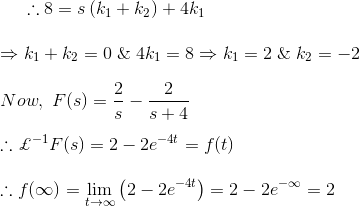
De ahí que se demuestre que de ambos métodos el valor final de la función se convierte en el mismo.
10) Encuentra la transformación de la función Laplace inversa,![]()
![]()
Solución
La F(s) puede ser reescrita como,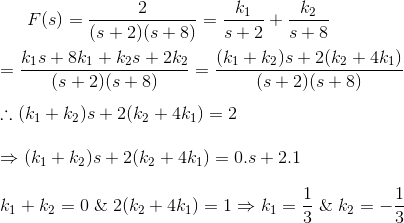
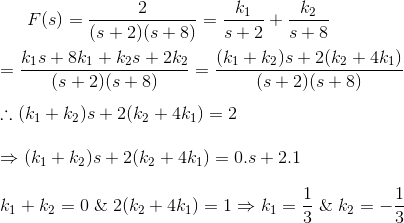
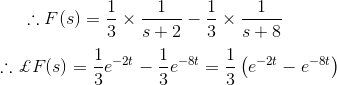
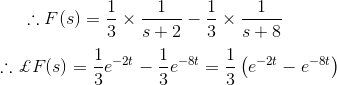
11) Encuentra la transformación Laplace inversa de![]()
![]()
Solución
La F(s) puede ser reescrita como,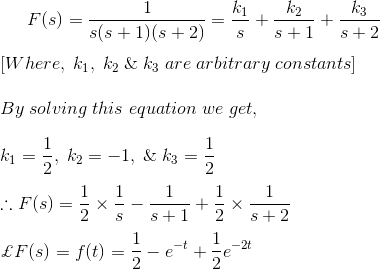
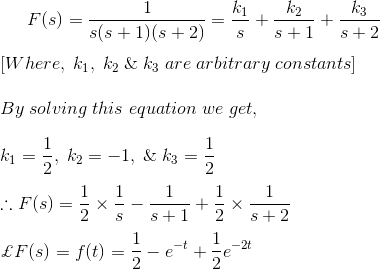
12) Encuentra la transformación Laplace inversa de![]()
![]()
Solución
La F(s) puede ser reescrita como,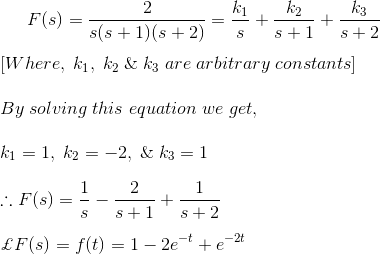
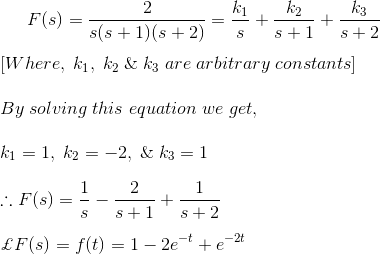
13) Expresar la ecuación diferencial en forma de transformación de Laplace![]()
![]()
Solución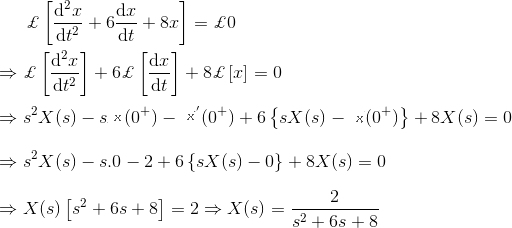
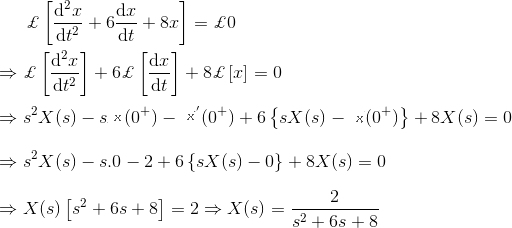
14) Expresar la ecuación diferencial en forma de transformación de Laplace![]()
![]()
Solución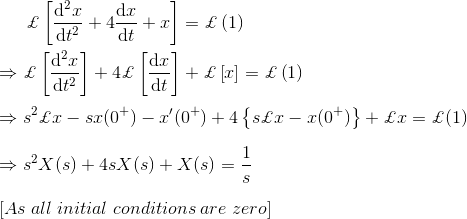
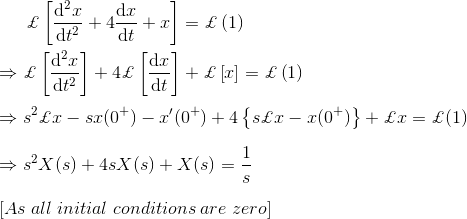
![]()
![]()
¿Dónde se usan las Transformaciones Laplace en la vida real?
El Laplace Transformar se deriva de la Ley de anulación de Lerchs. En el método de la Transformación Laplace, la función en el dominio del tiempo se transforma en una función Laplace en el dominio de la frecuencia. Esta función de Laplace tendrá la forma de una ecuación algebraica y puede ser resuelta fácilmente. La solución puede ser nuevamente transformada de nuevo al dominio del tiempo usando una Transformación Laplace inversa.
Esta transformación se utiliza más comúnmente para los sistemas de control, como se mencionó brevemente anteriormente. Las transformaciones se utilizan para estudiar y analizar sistemas como la ventilación, la calefacción y las condiciones del aire, etc. Estos sistemas se utilizan en todas las construcciones y edificios modernos.
Las transformaciones de Laplace también son importantes para los controles de procesos. Ayuda en el análisis de las variables que cuando se alteran producen los resultados requeridos. Un ejemplo de esto se puede encontrar en los experimentos relacionados con el calor.
Aparte de estos dos ejemplos, las transformaciones de Laplace se utilizan en muchas aplicaciones de ingeniería y es un método muy útil. Es útil tanto en la ingeniería electrónica como en la mecánica.
La acción de control de un sistema de control dinámico, ya sea eléctrico, mecánico, térmico, hidráulico, etc., puede representarse mediante una ecuación diferencial. La ecuación diferencial del sistema se deriva según las leyes físicas que rigen es un sistema. Para facilitar la solución de una ecuación diferencial que describe un sistema de control, la ecuación se transforma en una forma algebraica. Esta transformación se hace con la ayuda de la La transformación de Laplace es decir, la ecuación diferencial del dominio del tiempo se convierte en una ecuación algebraica del dominio de la frecuencia.
Una analogía interesante que puede ayudar a entender a Laplace es esta. Imagina que te encuentras con un poema inglés que no entiendes. Sin embargo, tienes un amigo español que es excelente para darle sentido a estos poemas. Así que traduces este poema al español y se lo envías, él a su vez explica este poema en español y te lo devuelve. Entiendes la explicación en español y entonces eres capaz de transferir el significado del poema al inglés y así entender el poema en inglés.
