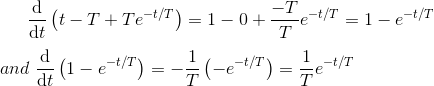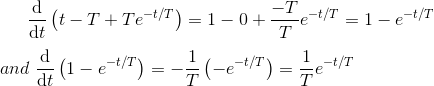En un sistema de control…puede haber algunos elementos de almacenamiento de energía adheridos a ella. Los elementos de almacenamiento de energía son generalmente inductores y condensadores en caso de un sistema eléctrico. Debido a la presencia de estos elementos de almacenamiento de energía, si el estado de energía del sistema es perturbado, tomará un cierto tiempo para cambiar de un estado de energía a otro. El tiempo exacto que tarda el sistema en cambiar de un estado de energía a otro se conoce como tiempo transitorio y el valor y patrón voltajes y corrientes durante este período se conocen como la respuesta transitoria.
Una respuesta transitoria se asocia normalmente a una oscilación, que puede ser sostenida o de naturaleza decadente. La naturaleza exacta del sistema depende de los parámetros del sistema. Cualquier sistema puede representarse con una ecuación diferencial lineal. La solución de esta ecuación diferencial lineal da la respuesta del sistema. La representación de un sistema de control por una ecuación diferencial lineal de funciones de tiempo y su solución se denomina colectivamente análisis en el dominio del tiempo del sistema de control.
Paso Función
Tomemos un independiente… fuente de tensión o un batería que está conectado a través de un voltímetro a través de un interruptor, s. Se ve claramente en la figura de abajo, cuando el interruptor s está abierto, el voltaje que aparece entre los terminales del voltímetro es cero. Si la tensión entre los terminales del voltímetro se representa como v (t), la situación puede representarse matemáticamente como

Ahora consideremos que a t = 0, el interruptor se cierra e instantáneamente el voltaje de la batería V voltio aparece a través del voltímetro y esa situación puede ser representada como,

Combinando las dos ecuaciones anteriores obtenemos![]()
![]()
En las ecuaciones anteriores si ponemos 1 en lugar de V, obtendremos una función de paso de unidad que puede ser definida como![]()
![]()
Ahora vamos a examinar el Laplace transformar de la función de paso de la unidad. La transformación de cualquier función puede obtenerse multiplicando esta función por e-st e integrándose multiplicado de 0 a infinito.
Fig 6.2.1![]()
![]()
Si la entrada es R(s), entonces![]()
![]()
Función de rampa
La función que se representa por una línea recta inclinada que intersecta el origen se conoce como función de rampa. Esto significa que esta función comienza de cero y aumenta o disminuye linealmente con el tiempo. Una función de rampa puede ser representada como,![]()
![]()
Aquí en esta ecuación anterior, k es la pendiente de la línea.
Fig 6.2.2
Ahora vamos a examinar el Laplace transformar de la función de rampa. Como dijimos antes, la transformación de Laplace de cualquier función se puede obtener multiplicando esta función por e-st e integrándose multiplicado de 0 a infinito.![]()
![]()
![]()
![]()
Función parabólica
Aquí, el valor de la función es cero cuando el tiempo t<0 y es cuadrático cuando el tiempo t > 0. Una función parabólica puede ser definida como,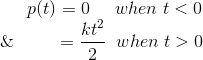
Ahora examinemos la transformación de Laplace de la función parabólica. Como dijimos antes, la transformación de Laplace de cualquier función se puede obtener multiplicando esta función por e-st e integrándose multiplicado de 0 a infinito.
Fig 6.2.3![]()
![]()
![]()
![]()
Función de impulso
La señal de impulso se produce cuando la entrada se aplica repentinamente al sistema durante un tiempo infinitesimal. La forma de onda de dicha señal se representa como una función de impulso. Si la magnitud de dicha función es unidad, entonces la función se denomina función de impulso unitario. La primera derivada temporal de la función de paso es la función de impulso. Por lo tanto, la transformación de Laplace de la función de impulso unitario no es más que la transformación de Laplace de la primera derivada temporal de la función de paso unitario.
Fig 6.2.4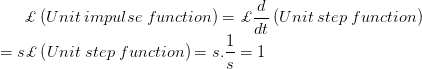
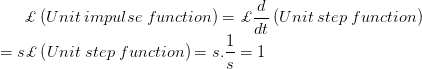
Respuesta temporal de los sistemas de control de primer orden
Cuando la potencia máxima de s en el denominador de una función de transferencia es uno, la función de transferencia representa un sistema de control de primer orden. Comúnmente, el sistema de control de primer orden puede ser representado como![]()
![]()
Tiempo de respuesta para la función de paso
Ahora se le da una entrada de paso unitario al sistema, entonces analicemos la expresión de la salida: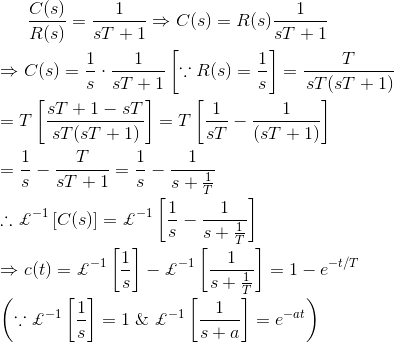
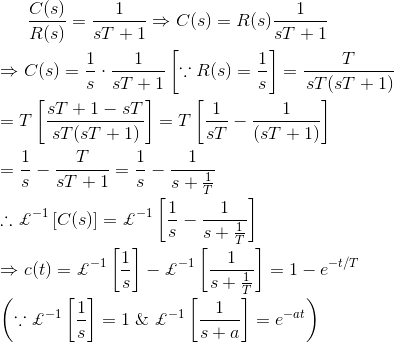
Fig 6.3.2 Se ve en la ecuación de error que si el tiempo se aproxima al infinito, la señal de salida llega exponencialmente al valor de estado estacionario de una unidad. Como la salida se aproxima a la entrada de forma exponencial, el error de estado estacionario es cero cuando el tiempo se aproxima al infinito.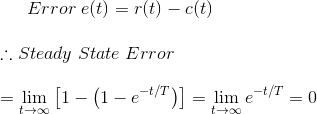
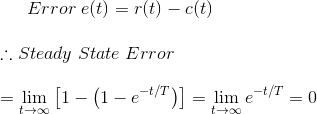
Pongamos t = T en la ecuación de salida y luego obtenemos,

Esta T se define como la constante de tiempo de la respuesta y la constante de tiempo de una señal de respuesta es el tiempo durante el cual la señal alcanza su 63,2% de su valor final. Ahora bien, si ponemos t = 4T en la anterior ecuación de respuesta de salida, entonces obtenemos,

Cuando el valor real de la respuesta alcanza el 98% del valor deseado, entonces se dice que la señal se alcanza en su condición de estado estable. Este tiempo requerido para alcanzar la señal hasta el 98 % de su valor deseado se conoce como tiempo de ajuste y naturalmente el tiempo de ajuste es cuatro veces la constante de tiempo de la respuesta. La condición de la respuesta antes del tiempo de ajuste se conoce como condición transitoria y la condición de la respuesta después del tiempo de ajuste se conoce como condición de estado estacionario. De esta explicación se desprende claramente que si la constante de tiempo del sistema es menor, la respuesta del sistema alcanza su condición de estado estacionario más rápidamente.
Tiempo de respuesta para la función de rampa
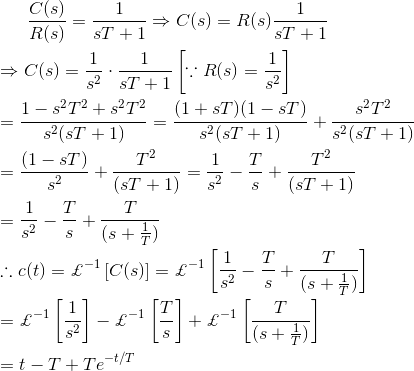
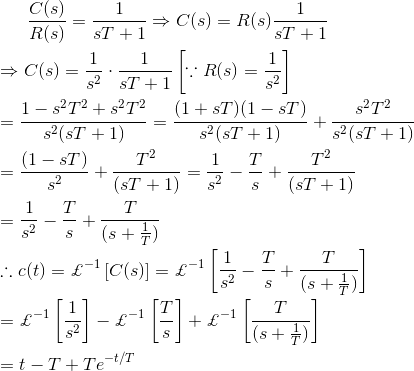
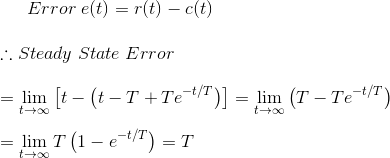
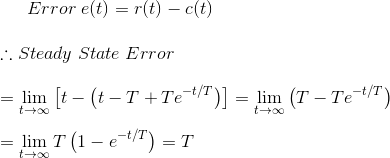
En este caso, durante la condición de estado estacionario, la señal de salida se retrasa con respecto a la de entrada en un tiempo igual a la constante de tiempo del sistema. Si la constante de tiempo del sistema es menor, el error de posición de la respuesta se hace menor.
Respuesta temporal para la función de impulso
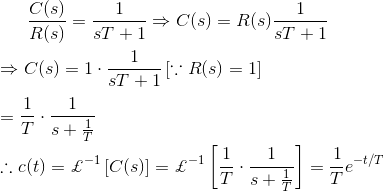
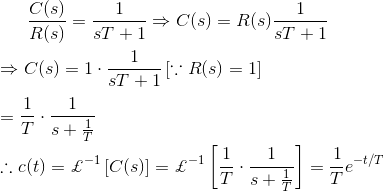
En la explicación anterior de la respuesta temporal del sistema de control, hemos visto que la función de paso es la primera derivada de la función de rampa y la función de impulso es la primera derivada de una función de paso. También se ha visto que la respuesta temporal de la función escalón es la primera derivada de la respuesta temporal de la función de rampa y la respuesta temporal de la función de impulso es la primera derivada de la respuesta temporal de la función escalón.