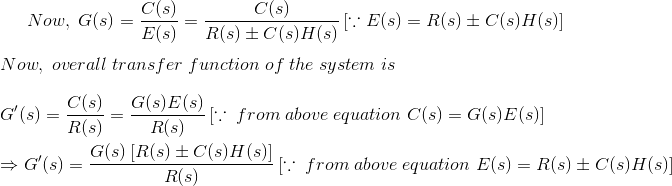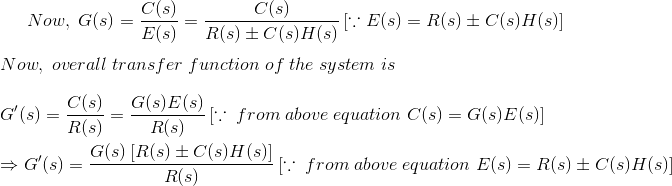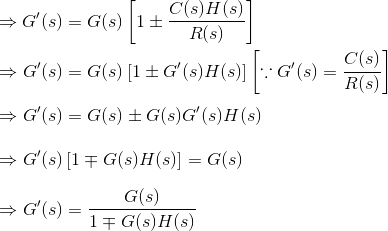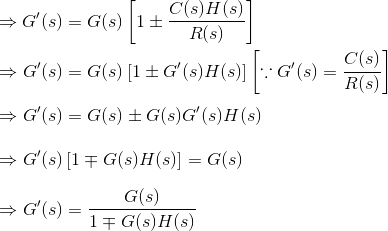El diagrama de bloques es representar a un sistema de control en forma de diagrama. En otras palabras, la representación práctica de un sistema de control es su diagrama de bloques. No siempre es conveniente derivar todo el función de transferencia de un complejo sistema de control en una sola función. Es más fácil y mejor derivar la función de transferencia del elemento de control conectado al sistema, por separado. El función de transferencia de cada elemento es entonces representado por un bloque y se conectan junto con el camino de flujo de señales. Para simplificar un sistema de control complejo, se utilizan diagramas de bloques. Cada elemento del sistema de control se representa con un bloque y el bloque es la representación simbólica de la función de transferencia de ese elemento. Un sistema de control completo puede representarse con un número necesario de bloques interconectados.
En la figura siguiente, hay dos elementos con función de transferencia Guno(s) y Gdos(s). Donde Gunos) es la función de transferencia del primer elemento y Gdoss) es la función de transferencia del segundo elemento del sistema.
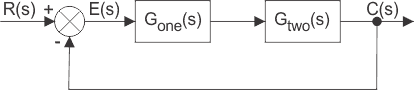

Además de eso, el diagrama también muestra que hay un camino de retroalimentación a través del cual la señal de salida C(s) es retroalimentada y comparada con la entrada R(s) y la diferencia entre la entrada y la salida es 
En cada bloque del diagrama, la salida y la entrada están relacionadas entre sí por una función de transferencia. Donde está la función de transferencia:![]()
![]()
Donde C(s) es la salida y R(s) es la entrada de ese bloque en particular.![]()
![]()
Un sistema de control complejo consiste en varios bloques. Cada uno de ellos tiene su propia función de transferencia. Pero la función de transferencia global del sistema es la relación entre la función de transferencia de la salida final y la función de transferencia de la entrada inicial del sistema. Esta función de transferencia global del sistema puede obtenerse simplificando el sistema de control mediante la combinación de estos bloques individuales, uno por uno.
La técnica de combinación de estos bloques se denomina técnica de reducción del diagrama de bloques. Para la aplicación exitosa de esta técnica, se deben seguir algunas reglas para la reducción del diagrama de bloques. Discutamos estas reglas, una por una para la reducción de diagrama de bloques del sistema de control. Si quiere hacer un estudio de los sistemas de control, vea nuestro sistemas de control MCQ.
Si la función de transferencia de la entrada del sistema de control es R(s) y la salida correspondiente es C(s), y la función de transferencia global del sistema de control es G(s), entonces el sistema de control puede representarse como:![]()
![]()
![]()
![]()
Despegue del diagrama de puntos de bloqueo
Cuando necesitamos aplicar una o la misma entrada a más de un bloque, usamos lo que se conoce como el punto de partida. Este punto es donde la entrada tiene más de un camino para propagarse. Obsérvese que la entrada no se divide en un punto, sino que la entrada se propaga por todos los caminos conectados a ese punto sin afectar su valor. Por lo tanto, al tener un punto de despegue las mismas señales de entrada pueden aplicarse a más de un sistema o bloque. La representación de una señal de entrada común a más de un bloque de un sistema de control se realiza mediante un punto común, como se muestra en la figura siguiente con el punto X.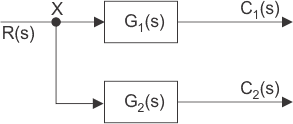

Bloques de cascada
Cuando se conectan varios sistemas o bloques de control en cascada, la función de transferencia de todo el sistema será el producto de la función de transferencia de todos los bloques individuales. Aquí también hay que recordar que la salida de cualquier bloque no se verá afectada por la presencia de otros bloques en el sistema en cascada.![]()
![]()
Ahora, del diagrama se ve que,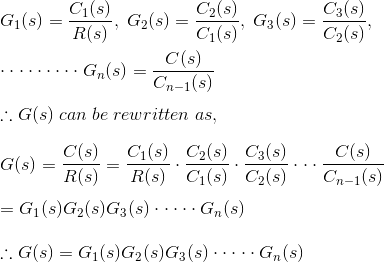
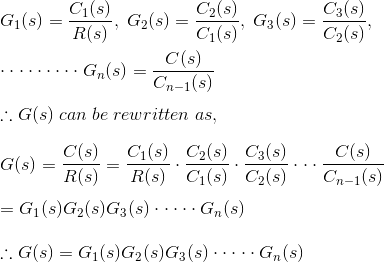
Donde, G(s) es la función de transferencia global del sistema de control en cascada.![]()
![]()
Suma de puntos del diagrama de bloques
En lugar de aplicar una sola señal de entrada a diferentes bloques como en el caso anterior, puede darse una situación en la que se apliquen diferentes señales de entrada al mismo bloque. En este caso, la señal de entrada resultante es la suma de todas las señales de entrada aplicadas. La suma de las señales de entrada se representa por un punto llamado punto de suma que se muestra en la figura siguiente por un círculo cruzado. Aquí R(s), X(s) e Y(s) son las señales de entrada. Es necesario indicar la multa que especifica la señal de entrada que entra en un punto de suma en el diagrama de bloques del sistema de control.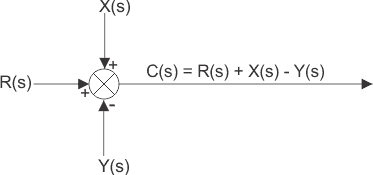

Punto de suma consecutiva
Un punto de suma con más de dos entradas puede dividirse en dos o más puntos de suma consecutivos, donde la alteración de la posición de los puntos de suma consecutivos no afecta a la salida de la señal. En otras palabras, si hay más de un punto de suma directamente interrelacionado, y entonces pueden intercambiarse fácilmente desde su posición sin afectar la salida final del sistema de suma.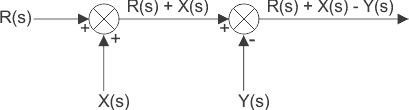
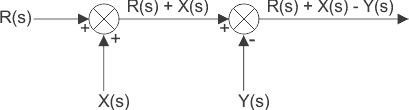
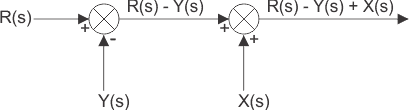

Bloques paralelos
Cuando a la misma señal de entrada se le aplican diferentes bloques y la salida de cada uno de ellos se suma en un punto de suma para tomar la salida final del sistema, entonces sobre toda la función de transferencia del sistema será la suma algebraica de la función de transferencia de todos los bloques individuales.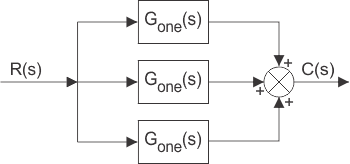

Si Cuno, Cdos y Ctres son las salidas de los bloques con la función de transferencia Guno, Gdos y GtresEntonces…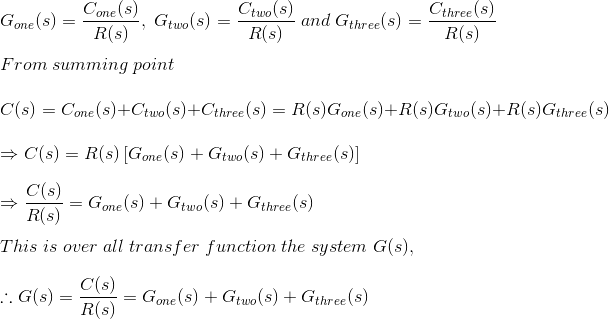
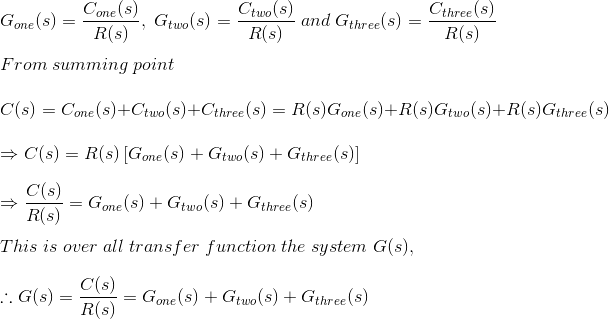
![]()
![]()
Desplazamiento del punto de despegue
Si se aplica la misma señal a más de un sistema, entonces la señal se representa en el sistema por un punto llamado punto de despegue. El principio de cambio de punto de despegue es que, puede ser desplazado a ambos lados de un bloque pero la salida final de las ramas conectadas al punto de despegue debe ser sin cambios. El punto de despegue puede ser desplazado a ambos lados del bloque.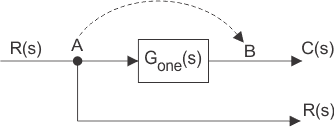

En la figura de arriba el punto de despegue se desplaza de la posición A a la B. La señal R(s) en el punto de despegue A se convertirá en G(s)R(s) en el punto B. Por lo tanto otro bloque de la función de transferencia inversa G(s) se pondrá en ese camino para obtener R(s) de nuevo.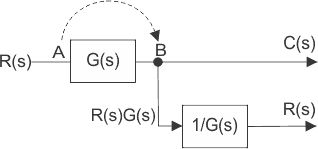

Ahora examinemos la situación cuando el punto de despegue se desplaza antes del bloque que estaba previamente después del bloque.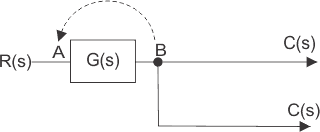

Aquí la salida es C(s) y la entrada es R(s) y por lo tanto![]()
![]()
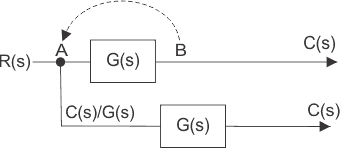

Aquí, tenemos que poner un bloque de la función de transferencia G(s) en el camino para que la salida venga de nuevo como C(s).![]()
![]()
Desplazamiento del punto de suma
Examinemos el desplazamiento del punto de suma desde una posición anterior a un bloque a una posición posterior a un bloque. Hay dos señales de entrada R(s) y X(s) que entran en un punto de suma en la posición A. La salida del punto de suma es R(s) X(s). La señal resultante es la entrada de un bloque del sistema de control de la función de transferencia G(s) y la salida final del sistema es

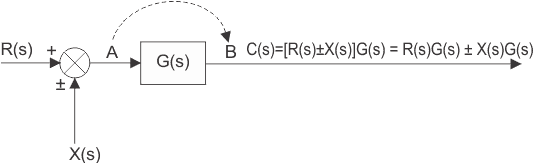

Por lo tanto, un punto de suma puede ser redibujado con las señales de entrada R(s)G(s) y X(s)G(s)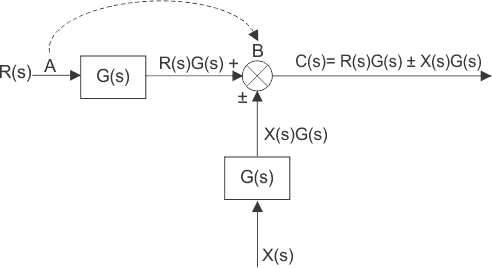

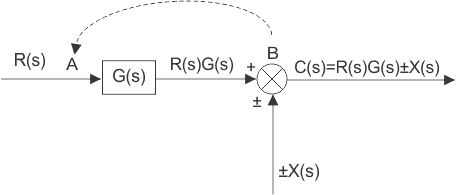

En los diagramas de bloques anteriores de la salida del sistema de control se puede reescribir como![]()
![]()
La ecuación anterior puede ser representada por un bloque de la función de transferencia G(s) y la entrada R(s) X(s)/G(s) de nuevo R(s)X(s)/G(s) puede ser representada con un punto de suma de la señal de entrada R(s) y X(s)/G(s) y finalmente puede ser dibujada como se muestra a continuación.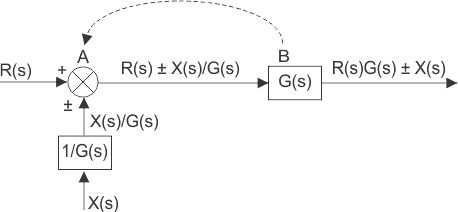

Diagrama de bloques del sistema de control de bucle cerrado
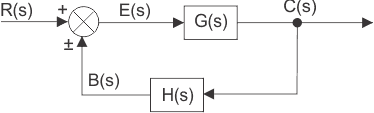

En un sistema de control de circuito cerradouna fracción de la salida se retroalimenta y se añade a la entrada del sistema. Si H (s) es la función de transferencia de la trayectoria de retroalimentación, entonces la función de transferencia de la señal de retroalimentación será B(s) = C(s)H(s). En el punto de suma, la señal de entrada R(s) se sumará a B(s) y producirá la señal de entrada real o la señal de error del sistema y se denota por E(s).