En el presente artículo trataremos todo lo relacionado con las señales discretas, que están compuestas por datos discretos o datos muestreados o también conocidas como datos digitales del sistema de control. Ahora bien, antes de discutir este tema en detalle es muy esencial saber, ¿cuál es la necesidad de una tecnología digital a pesar de que tenemos sistemas analógicos?
Así que discutamos primero algunas ventajas del sistema digital sobre el analógico.
- El consumo de energía es menor en el sistema digital en comparación con el sistema analógico.
- Los sistemas digitales pueden manejar fácilmente los sistemas no lineales, lo cual es la ventaja más importante de datos digitales en el sistema de control.
- Los sistemas digitales trabajan en las operaciones lógicas debido a esto muestran la propiedad de la toma de decisiones que es muy útil en el mundo actual de las máquinas.
- Son más fiables en comparación con los sistemas analógicos.
- Los sistemas digitales son fáciles de conseguir en tamaño compacto y tienen un peso ligero.
- Trabajan con instrucciones que podemos programar según nuestras necesidades, por lo que son más versátiles que los sistemas analógicos.
- Diversas tareas complejas pueden realizarse fácilmente con la ayuda de la tecnología digital con un alto grado de precisión.
Supongamos que tienes una señal continua, entonces ¿cómo convertirás esta señal continua en señales discretas? La respuesta a esta pregunta es muy simple con la ayuda del proceso de muestreo.
Proceso de muestreo
El proceso de muestreo se define como la conversión de la señal analógica en la digital con la ayuda de un interruptor (también conocido como sampler). Un sampler es un interruptor continuo de encendido y apagado que convierte directamente las señales analógicas en señales digitales. Podemos tener una conexión en serie del sampler dependiendo de la conversión de las señales que utilizamos. Para un sampler ideal, el ancho del pulso de salida es muy pequeño (tiende a cero). Ahora bien, cuando se habla de sistema discreto es muy importante conocer las transformaciones z. Discutiremos aquí sobre las transformaciones z y sus utilidades en el sistema discreto. El papel de la transformación z en los sistemas discretos es el mismo que Transformación de Fourier en sistemas continuos. Ahora discutamos la transformación z en detalle.
Definimos la transformación z como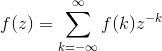
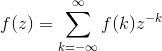
Donde, F(k) es un dato discreto
Z es un número complejo
F (z) es la transformación de Fourier de f (k).
Las propiedades importantes de la transformación z están escritas a continuación
Linealidad
Consideremos la suma de dos funciones discretas f (k) y g (k) de tal manera que

de tal manera que p y q son constantes, ahora al tomar la Laplace transformar que tenemos por la propiedad de la linealidad:

Cambio de escala: consideremos una función f(k), al tomar la transformación z que tenemos

entonces tenemos por propiedad de cambio de escala![]()
![]()
Propiedad cambiante: Según esta propiedad

Ahora discutamos algunas importantes transformaciones z y sugeriré a los lectores que aprendan estas transformaciones:

La transformación de esta función es de 1/s2 y la correspondiente f(k) = kT. Ahora la transformación z de esta función es![]()
![]()
Función f (t) = t2: La transformación de Laplace de esta función es de 2/s3 y la correspondiente f(k) = kT. Ahora la transformación z de esta función es![]()
![]()


La transformación de esta función es 1/(s + a) y la correspondiente f(k) = e(-akT). Ahora la transformación z de esta función es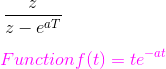
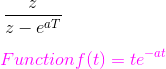
La transformación de esta función es 1/(s + a)2 y la correspondiente f(k) = Te-akT. Ahora la transformación z de esta función es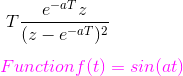
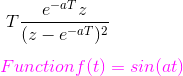
La transformación de esta función es a/(s)2 + a2) y el correspondiente f(k) = sin(akT). Ahora la transformación z de esta función es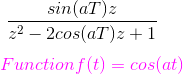
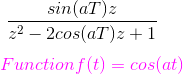
La transformación de esta función es s/(s)2 + a2) y el correspondiente f(k) = cos(akT). Ahora la transformación z de esta función es![]()
![]()
Ahora bien, en algún momento es necesario volver a tomar muestras de datos, lo que significa convertir los datos discretos en continuos. Podemos convertir los datos digitales del sistema de control en forma continua mediante los circuitos de retención que se discuten a continuación:
Retenga los circuitos: Estos son los circuitos que convierten los datos discretos en datos continuos o datos originales. Ahora hay dos tipos de circuitos de retención y se explican en detalle:
Circuito de retención de orden cero
A continuación se muestra la representación en forma de diagrama de bloques del circuito de retención de orden cero:
Figura relacionada con la retención de orden cero.
En el diagrama de bloques hemos dado una entrada f(t) al circuito, cuando permitimos que la señal de entrada pase a través de este circuito reconvierte la señal de entrada en una continua. La salida del circuito de retención de orden cero se muestra a continuación.
Ahora estamos interesados en averiguar la función de transferencia del circuito de retención de orden cero. Al escribir la ecuación de salida tenemos

en la toma de la Laplace transformar de la ecuación anterior tenemos![]()
![]()
A partir de la ecuación anterior podemos calcular la función de transferencia como![]()
![]()
Al sustituir s=j podemos dibujar el gráfico de bode para el circuito de retención de orden cero. A continuación se muestra la representación eléctrica del circuito de retención de orden cero, que consiste en un muestreador conectado en serie con un resistencia y esta combinación está conectada con una combinación paralela de resistencia y condensador.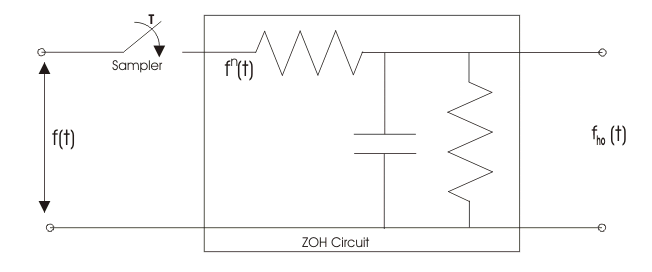

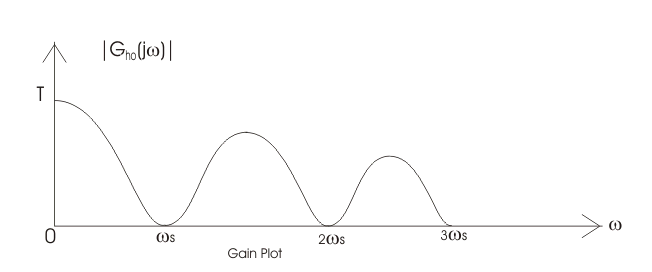
 Curva de respuesta en frecuencia del ZOH
Curva de respuesta en frecuencia del ZOH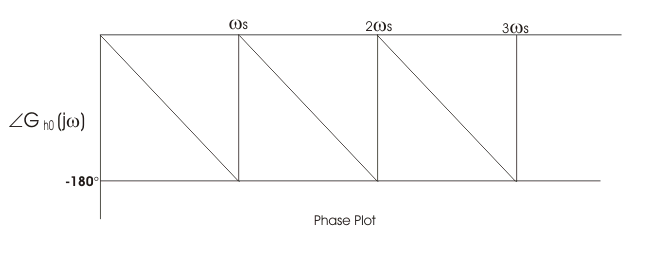

Curva de respuesta de frecuencia del ZOH
Circuito de retención de primera orden
La representación del diagrama de bloques del circuito de retención de primer orden se da a continuación:
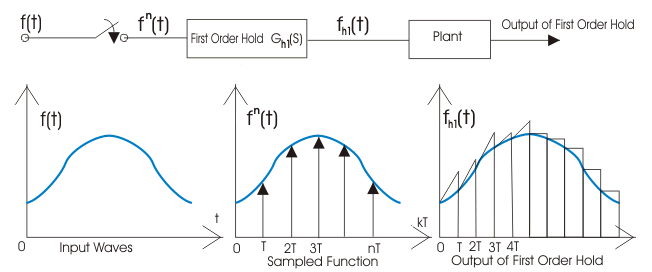

Circuito de retención de primera orden
En el diagrama de bloques hemos dado una entrada f(t) al circuito, cuando permitimos que la señal de entrada pase a través de este circuito reconvierte la señal de entrada en una continua. La salida del circuito de retención de primer orden se muestra a continuación: Ahora estamos interesados en averiguar la función de transferencia del circuito de retención de primer orden. Al escribir la ecuación de salida tenemos![]()
![]()
Al tomar el Laplace transformar de la ecuación anterior tenemos![]()
![]()
A partir de la ecuación anterior podemos calcular la función de transferencia como (1-e-sT)/s. al sustituir s=j podemos dibujar el gráfico de bode para el circuito de retención de orden cero. A continuación se muestra el diagrama de código del circuito de retención de primer orden, que consiste en un diagrama de magnitud y un diagrama de ángulo de fase. El diagrama de magnitud comienza con el valor de magnitud 2/s.
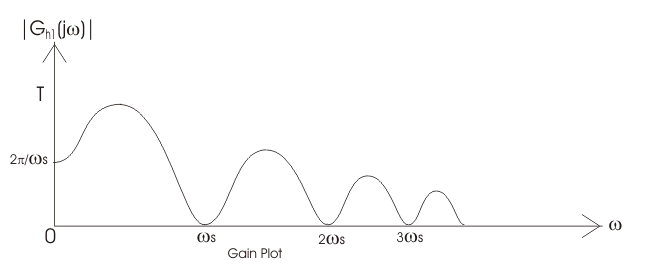

Gráfico de ganancia del circuito de retención de primer orden