¿Qué es el criterio de Nyquist
Criterio de estabilidad del níquel (o Criterios de Nyquist) es una técnica gráfica utilizada en ingeniería de control para determinar la estabilidad de un sistema dinámico. Como el criterio de estabilidad de Nyquist sólo considera la La trama de Nyquist de sistemas de control de circuito abiertopuede aplicarse sin computar explícitamente los polos y ceros del sistema de bucle cerrado o abierto.
Por consiguiente, los criterios de Nyquist pueden aplicarse a sistemas definidos por funciones no racionales (como los sistemas con retrasos). A diferencia de Gráficas de Bodepuede manejar funciones de transferencia con singularidades en el medio plano derecho.
El criterio de estabilidad del níquel puede expresarse como:
Z = N + P
Dónde:
- Z = número de raíces de 1+G(s)H(s) en el lado derecho (RHS) del plano s (También se llama ecuación de ceros de características)
- N = número de encierro del punto crítico 1+j0 en el sentido de las agujas del reloj
- P = número de polos de la función de transferencia de bucle abierto (OLTF) [es decir, G(s)H(s)] en RHS del plano s.
La condición anterior (es decir, Z=N+P) es válida para todos los sistemas, ya sean estables o inestables.
Ahora explicaremos este criterio con ejemplos del criterio de estabilidad de Nyquist.
Ejemplos del Criterio de Estabilidad del Níquel
Ejemplo 1
Considere una función de transferencia de bucle abierto (OLTF) como 
¿Es un sistema estable o inestable. Tal vez la mayoría de ustedes dirá que es un sistema inestable porque un polo está en +2. Sin embargo, tened en cuenta que la estabilidad depende del denominador de la función de transferencia de bucle cerrado Si alguna raíz del denominador de la función de transferencia de bucle cerrado (también llamada ecuación de características) está en el RHS del plano s, entonces el sistema es inestable. Por lo tanto, en el caso anterior, un polo en +2 tratará de llevar el sistema hacia la inestabilidad, pero el sistema puede ser estable. Aquí la gráfica de Nyquist es útil para encontrar la estabilidad.
Según la teoría de Nyquist Z=N+P (para cualquier sistema, ya sea estable o inestable).
Para el sistema estable, Z=0, es decir, ninguna raíz de la ecuación de las características debe estar en RHS.
Así que para el sistema estable N = –P.
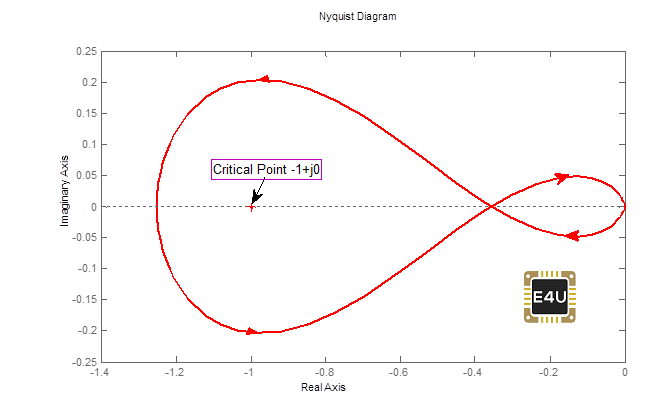
La gráfica de Nyquist del sistema anterior es como se muestra a continuación
Código del laboratorio de la trama de Nyquist
s = tf('s')G1 = 120 / ((s-2)*(s+6)*(s+8))nyquist(G1, 'rojo')
Según el diagrama, la trama de Nyquist rodea el punto –1+j0 (también llamado punto crítico) una vez en la dirección contraria al reloj. Por lo tanto N= –1, En OLTF, un polo (a +2) está en RHS, por lo tanto P =1. Puedes ver que N= –P, por lo tanto el sistema es estable.
Si se encuentran las raíces de la ecuación de las características, será –10.3, –0.86j1.24. (es decir, el sistema es estable), y Z=0. Se puede hacer una pregunta, si se puede encontrar la ecuación de las raíces de las características, para que podamos comentar la estabilidad sobre esa base, entonces cuál es la necesidad de la gráfica de Nyquist. La respuesta es que, cuando no se disponía de software, en aquellos tiempos la gráfica de Nyquist era muy útil.
Ejemplo 2
Ahora toma otro ejemplo: 
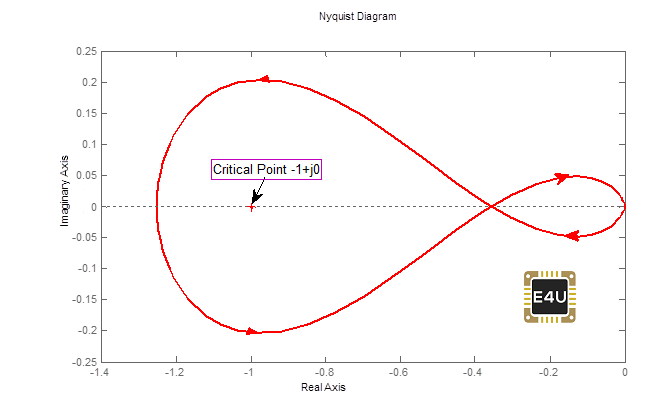
La trama de Nyquist es la siguiente:
Código del laboratorio de la trama de Nyquist
s = tf('s')G2 = 100 / ((s-2)*(s+6)*(s+8))nyquist(G2, 'rojo')
De la figura, se puede encontrar que N= –1. (El círculo de la trama de Nyquist del punto crítico es uno en la dirección contraria al reloj)
En este ejemplo también P=1. (un polo de OLTF en RHS)
Así que, N=–P. Por lo tanto, el sistema es estable.
(Las raíces de la ecuación de las características son –10.04, –1.72, – 0.23)
Ejemplo 3
Ahora toma otro ejemplo: 
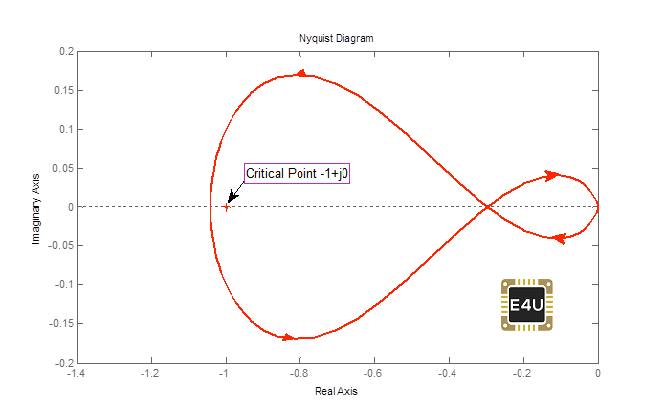
Aquí de nuevo P=1.
La trama de Nyquist es la siguiente:
Código del laboratorio de la trama de Nyquist
s = tf('s')G3 = 50 / ((s-2)*(s+6)*(s+8))nyquist(G3, 'rojo')
Se puede ver N=0. (No hay cerco del punto crítico). Como N no es igual a P, por lo tanto el sistema es inestable. (Las raíces de la ecuación de las características son –9.32, –3,92, 1,255) es decir, Z=1 (un polo a 1,255 está en RHS).
Así que, puedes entender, la condición Z=N+P es válida para todos los sistemas.
Ejemplo 4
Ahora considera 
Si dibujas su trama de Nyquist, pasará por el punto crítico (–1+j0). En este caso el sistema es marginalmente estable. Se puede entender que N está indefinido en este caso (En el presente caso dos raíces de la ecuación de las características estarán en el origen y una raíz en el lado izquierdo del plano s. Por lo tanto el sistema será marginalmente estable).
En todos los ejemplos anteriores se puede ver que el denominador es el mismo, pero el numerador es diferente, o digamos que el numerador es variable. Por lo tanto, consideremos la siguiente función de transferencia en bucle abierto: 
Si se aplica el Criterio de Routh Hurwitz a la ecuación de características 1+G(s)H(s), entonces se encontrará el rango de K como 96
Así que ahora puedes entender por qué los sistemas de los ejemplos 1–4 son estables, inestables o marginalmente estables.
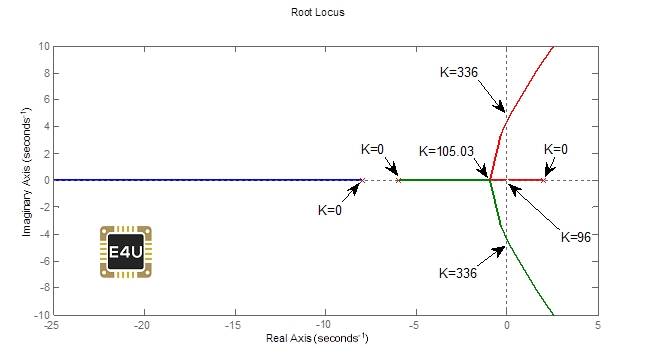
Puedes dibujar el lugar de la raíz de la función de transferencia anterior, será:
Código del laboratorio de la trama de Nyquist
s = tf('s')G4 = 1 / ((s-2)*(s+6)*(s+8))rlocus(G4)
(Las ramas de los loci de la raíz comienzan en 2, -6, -8, donde K=0. Así que puedes ver que para K<96, un polo de la función de transferencia de bucle cerrado está en RHS del plano s, por lo tanto para K<96 el sistema es inestable. El sistema es estable para 96
Tenga en cuenta la siguiente declaración:
El margen de ganancia (GM) y el margen de fase (PM) son positivos si el sistema es estable, negativos si el sistema es inestable y ambos son cero si el sistema es marginalmente estable. Cuanto más alto es el GM & PM, más estable es el sistema (Esta es la razón, las mediciones de GM & PM se llaman estabilidad relativa).
Pero la afirmación anterior es cierta si ningún polo del OLTF está en el RHS del avión S. En todos los ejemplos anteriores un polo de OLTF está en +2; en este tipo de sistemas el criterio de estabilidad de Nyquist es útil.
Ahora retomaremos algunos ejemplos más:
Ejemplo 5
Considere 
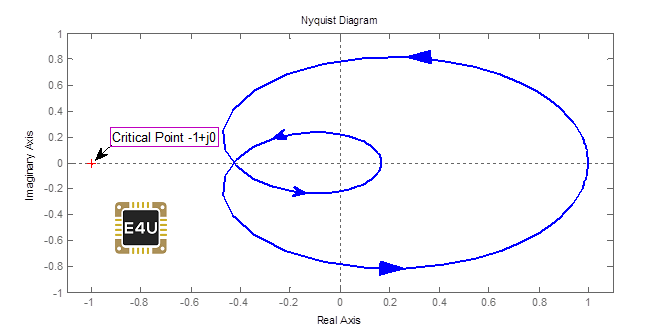
Su trama de Nyquist es la siguiente:
Código del laboratorio de la trama de Nyquist
s = tf('s')G5 = ((s+1)*(s+2)) / ((s-3)*(s-4))nyquist(G5, 'rojo')
Según la función de transferencia P=2 (dos polos de OLTF en RHS)
Según la trama de Nyquist N=0
Por lo tanto Z=N+P=2; implica que dos polos del bucle cerrado de transferencia funcionan en RHS del plano s, por lo que el sistema es inestable.
Ejemplo 6
Considere 
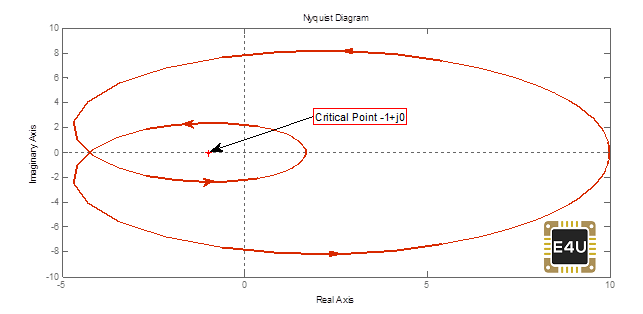
Su trama de Nyquist es la siguiente:
Código del laboratorio de la trama de Nyquist
s = tf('s')G6 = (10*(s+1)*(s+2)) / ((s-3)*(s-4))nyquist(G6, 'rojo')
Según la función de transferencia P=2 (dos polos de OLTF en RHS)
Según la trama de Nyquist N=–2
Por lo tanto, Z=N+P=0; implica que ningún polo de la función de transferencia de bucle cerrado en el RHS del plano s, por lo tanto el sistema es estable.
Tenga en cuenta que hemos utilizado la fórmula Z=N+P, donde N=número de encierro del punto crítico 1+j0 en el sentido de las agujas del reloj. En algunos libros, se puede encontrar la fórmula Z=N+P, donde N=número de encierro del punto crítico 1+j0 en sentido contrario a las agujas del reloj. Ambas son correctas.
