AC Motores de inducción ofrecen características operativas envidiables como la robustez, la fiabilidad y la facilidad de control. Se utilizan ampliamente en diversas aplicaciones que van desde los sistemas de control de movimiento industrial hasta los electrodomésticos. Sin embargo, el uso de motores de inducción en su máxima eficiencia es una tarea difícil debido a su complejo modelo matemático y a su característica no lineal durante la saturación. Estos factores dificultan el control de los motores de inducción y exigen el uso de algoritmos de control de alto rendimiento, como el control vectorial.
Introducción del control orientado al campo
El control escalar como la estrategia V/Hz tiene sus limitaciones en términos de rendimiento. El método de control escalar para los motores de inducción genera oscilaciones en el par producido. Por lo tanto, para lograr un mejor rendimiento dinámico, se necesita un esquema de control más superior para el motor de inducción. Con las capacidades de procesamiento matemático que ofrecen los microcontroladores, los procesadores de señales digitales y los FGPA, se pueden implementar estrategias de control avanzadas para desacoplar la generación de par y las funciones de magnetización en un motor de inducción de CA. Este par de torsión desacoplado y flujo de magnetización es comúnmente llamado rotor Control orientado al flujo (FOC).
Control orientado al campo describe la forma en que el control del par y la velocidad se basa directamente en el estado electromagnético del motor, similar a un Motor de corriente continua. FOC es la primera tecnología para controlar las variables reales de control del motor de par y flujo. Con el desacoplamiento entre el estator actual (flujo magnetizante y torque), el componente productor de torque del flujo del estator puede ser controlado independientemente. Desacoplando el control, a bajas velocidades, el estado de magnetización del motor puede mantenerse al nivel apropiado, y el par puede ser controlado para regular la velocidad.
FOC ha sido desarrollado únicamente para aplicaciones de motores de alto rendimiento que pueden funcionar sin problemas en un amplio rango de velocidades, pueden producir un par completo a velocidad cero y son capaces de una rápida aceleración y desaceleración.
Principio de trabajo del control orientado al campo
El control orientado al campo consiste en controlar las corrientes estatóricas representadas por un vector. Este control se basa en proyecciones que transforman un sistema trifásico dependiente del tiempo y la velocidad en un sistema invariante de tiempo de dos coordenadas (trama d y q). Estas transformaciones y proyecciones conducen a una estructura similar a la del control de una máquina de corriente continua. Las máquinas BDC necesitan dos constantes como referencias de entrada: la componente de par (alineada con la q coordinar) y el componente de flujo (alineado con d coordinar).
Los voltajes trifásicos, corrientes y flujos de los motores de CA pueden ser analizados en términos de complejos vectores espaciales. Si tomamos ia, ib, ic como corrientes instantáneas en las fases del estator, entonces el estator actual El vector se define como sigue:

Donde, (a, b, c) son los ejes de sistema trifásico.
Este actual El vector espacial representa el sistema sinusoidal trifásico. Necesita ser transformado en un sistema de coordenadas invariable de dos tiempos. Esta transformación puede dividirse en dos pasos:
(a, b, c) (, ) (la transformación de Clarke), que da resultados de un sistema de dos variantes de tiempo de coordenadas.
(a, ) (d, q) (la transformación de Park), que da resultados de un sistema invariante de tiempo de dos coordenadas.
La (a, b, c) (, ) Proyección (transformación de Clarke)
Cantidades trifásicas o voltajes o corrientes, que varían en el tiempo a lo largo de los ejes a, b y c pueden transformarse matemáticamente en voltajes o corrientes bifásicos, que varían en el tiempo a lo largo de los ejes y por la siguiente matriz de transformación: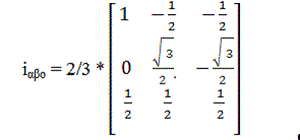
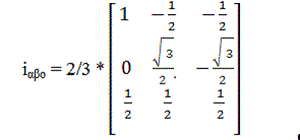
Asumiendo que el eje a y el eje están en la misma dirección y es ortogonal a ellos, tenemos el siguiente diagrama vectorial: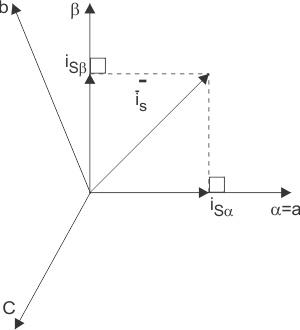

La proyección anterior modifica la sistema trifásico en el sistema ortogonal de dos dimensiones (, ) como se indica a continuación: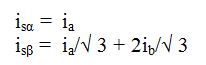
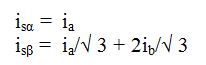
Pero estas dos corrientes de fase (, ) siguen dependiendo del tiempo y la velocidad.
La proyección (, ) (d.q) (Transformación del parque)
Esta es la transformación más importante en el BDC. De hecho, esta proyección modifica el sistema ortogonal fijo de dos fases (, ) en el sistema de referencia giratorio d, q. La matriz de transformación se muestra a continuación: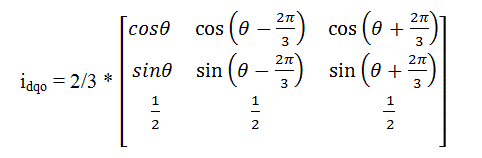
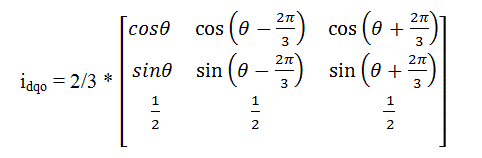
Donde, es el ángulo entre el sistema de coordenadas rotativas y fijas.
Si se considera que el eje d está alineado con el flujo del rotor, la figura 2 muestra la relación de los dos marcos de referencia para el actual vector: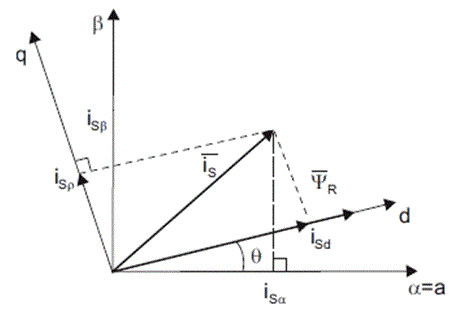

¿Dónde está la posición del flujo del rotor? Los componentes de par y flujo del actual vector se determinan mediante las siguientes ecuaciones: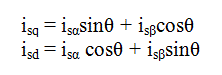
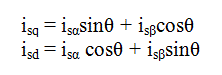
Estos componentes dependen de los componentes del vector de corriente (, ) y de la posición del flujo del rotor. Si se conoce la posición exacta del flujo del rotor, entonces, mediante la ecuación anterior, la componente d, q puede ser fácilmente calculada. En este instante, el par puede ser controlado directamente porque la componente de flujo (isd) y el componente de par (isq) son independientes ahora.
Módulo básico para el control orientado al campo
Se miden las corrientes de fase estatorial. Estas corrientes medidas se introducen en el bloque de transformación de Clarke. Los resultados de esta proyección se titulan is y yos. Estos dos componentes de la corriente entran en el bloque de transformación de Park que proporciona actual en el marco de referencia d, q. La isd y yosq los componentes se contrastan con las referencias: isdref (la referencia de flujo) y isqref (la referencia del par de torsión). En este momento, la estructura de control tiene una ventaja: puede utilizarse para controlar máquinas síncronas o de inducción simplemente cambiando la referencia de flujo y siguiendo la posición del flujo del rotor. En el caso del PMSM, el flujo del rotor está determinado por los imanes, por lo que no es necesario crear uno. Por lo tanto, mientras se controla un PMSM, isdref debería ser igual a cero. Como motores de inducción necesitan la creación de un flujo de rotor para poder funcionar, la referencia de flujo no debe ser igual a cero. Esto elimina fácilmente uno de los principales defectos de las estructuras de control clásicas: la portabilidad de los accionamientos asíncronos a los síncronos. Las salidas de los controladores PI son Vsdref y Vsqref. Se aplican al bloque de transformación de Park inverso. Los resultados de esta proyección son Vsref y Vsref se alimentan al bloque de algoritmos de modulación de ancho de pulso del vector espacial (SVPWM). Las salidas de este bloque proporcionan señales que impulsan el inversor. Aquí, tanto las transformaciones de Park como las de Park inverso necesitan la posición del flujo del rotor. Por lo tanto, la posición del flujo del rotor es la esencia del BDC.
La evaluación de la posición del flujo del rotor es diferente si consideramos el motor síncrono o de inducción.
- En caso de motor(es) síncrono(s)la velocidad del rotor es igual a la velocidad del flujo del rotor. Entonces la posición del flujo del rotor está directamente determinada por la posición sensor o por la integración de la velocidad del rotor.
- En caso de motor asíncrono(s), la velocidad del rotor no es igual a la velocidad del flujo del rotor debido al deslizamiento; por lo tanto, se utiliza un método particular para evaluar la posición del flujo del rotor (). Este método utiliza actual que necesita dos ecuaciones del modelo motor de inducción modelo en el marco de referencia rotativo d,q.
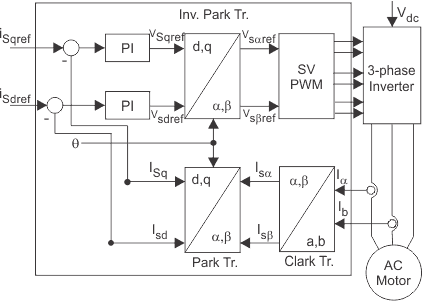

Diagrama de bloques de BDC simplificado e indirecto
Clasificación del control orientado al campo
BDC para el motor de inducción puede clasificarse en dos tipos: Esquemas de BDC indirecta y BDC directa. En la estrategia de BDC el vector de flujo del rotor se mide por medio de un sensor de flujo montado en el espacio de aire o utilizando el voltaje ecuaciones a partir de los parámetros de la máquina eléctrica. Pero en el caso de IFOC el vector de flujo del rotor se estima usando el control orientado al campo ecuaciones (modelo actual) que requieren una medición de la velocidad del rotor. Entre ambos esquemas, la IFOC se utiliza más comúnmente porque en el modo de lazo cerrado puede funcionar fácilmente en todo el rango de velocidad desde la velocidad cero hasta el debilitamiento de campo de alta velocidad.
Ventajas del control orientado al campo
- Respuesta de torsión mejorada.
- Control del par a bajas frecuencias y baja velocidad.
- Precisión de la velocidad dinámica.
- Reducción del tamaño del motor, del coste y del consumo de energía.
- Operación de cuatro cuadrantes.
- Capacidad de sobrecarga a corto plazo.