Análisis del error de estado estacionario en un sistema de control

¿Qué es el error de estado estacionario?

Error de estado estable se define como la diferencia entre el valor deseado y el valor real de la salida de un sistema en el límite a medida que el tiempo pasa al infinito (es decir, cuando la respuesta del sistema de control ha alcanzado el estado estable).

El error en estado constante es una propiedad de la respuesta de entrada/salida para un sistema lineal. En general, un buen sistema de control será aquel que tenga un bajo error de estado estacionario.

Primero, discutiremos el error de estado estacionario en una función de transferencia de primer orden analizando su respuesta de estado estacionario. Consideremos la función de transferencia a continuación:

Este es un simple función de transferencia de primera ordencon una ganancia igual a uno y una constante de tiempo de 0,7 segundos. Nótese que se conoce como una función de transferencia de primer orden porque la s en el denominador tiene la mayor potencia de 1. Si en cambio fuera sería una función de transferencia de segundo orden.

La respuesta de esta función de transferencia a una entrada de estado estacionario se muestra en la Figura-1. Se puede ver que en estado estacionario, la salida es exactamente igual a la entrada. Por lo tanto, el error de estado estacionario es cero.

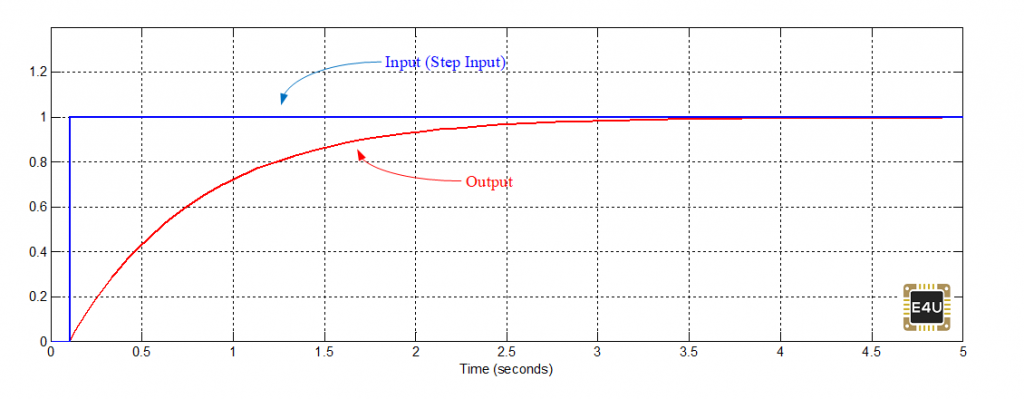
La respuesta de esta función a una entrada de rampa de la unidad se muestra en la Figura-2. Se puede ver que en estado estable hay una diferencia entre la entrada y la salida. Por lo tanto, para una entrada de rampa de la unidad, existe un error de estado estacionario.

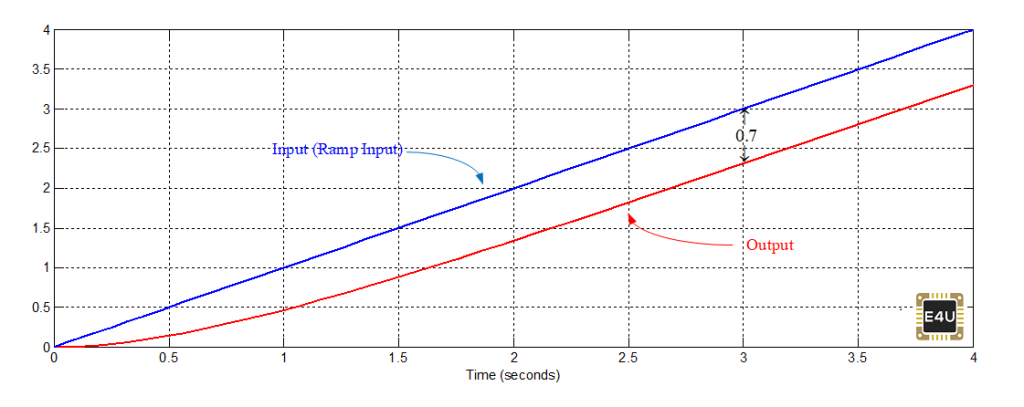
Obsérvese que en muchos libros de sistemas de control se puede encontrar que contra la entrada de rampa, el error de estado estacionario de una función de transferencia de primer orden es igual a la constante de tiempo. Al observar la Figura-2 anterior, podemos ver que esto es cierto. A t=3 segundos, la entrada es 3 mientras que la salida es 2.3. Por lo tanto, el error de estado estacionario es 0,7, que es igual a la constante de tiempo de esta función de transferencia de primer orden.

Por favor, tenga en cuenta los siguientes consejos importantes:

• El error de estado constante es mayor si la entrada es parabólica, es generalmente menor para la entrada de rampa, y es aún más bajo para una entrada de paso. Al igual que en la explicación anterior, el error de estado constante es cero para la entrada de paso, y 0,7 para la entrada de rampa y se puede encontrar que es contra la entrada parabólica.
• Cabe señalar que el error de estado estacionario depende de la entrada, mientras que la estabilidad no depende de la entrada.

Consideremos un sistema de control de circuito cerrado con función de transferencia

Donde los símbolos tienen su significado habitual. La estabilidad del sistema depende del denominador, es decir, 1+G(s)H(s). 1+G(s)H(s) = 0 se denomina ecuación de características. Sus raíces indican la estabilidad del sistema. El error de estabilidad depende de R(s).

En un sistema de control de bucle cerrado la señal de error puede ser calculada como El error de estado estacionario se puede encontrar como ess= donde el error en estado estacionario es el valor de la señal de error en estado estacionario. A partir de esto podemos ver que el error de estado estacionario depende de R(s).

• Como se mencionó anteriormente, la estabilidad depende del denominador, es decir, 1 + G(s)H(s). Aquí 1 es constante, por lo tanto la estabilidad depende de G(s)H(s), que es la parte de la ecuación que puede cambiar. Por lo tanto, puedes entender la gráfica de Bode, la gráfica de Nyquist se dibuja con la ayuda de G(s)H(s), pero indican la estabilidad de .
• G(s)H(s) se llama una función de transferencia de bucle abierto y se llama función de transferencia en bucle cerrado. Mediante el análisis de la función de transferencia de bucle abierto, es decir, G(s)H(s), podemos encontrar la estabilidad de una función de transferencia de bucle cerrado a través del gráfico de Bode y el gráfico de Nyquist.

Ahora, explicaremos, el error de estado estacionario en el sistema de control de bucle cerrado con algunos ejemplos numéricos:

Ejemplo 1:

Considere el siguiente sistema de control (sistema-1) como se muestra en la Figura-3:

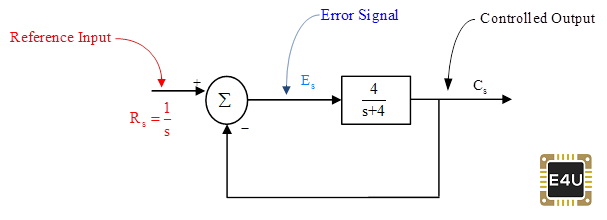
Entrada de referencia Rses una entrada de paso de unidad.

En la figura 4 se muestran varios valores de estado estable del Sistema-1.

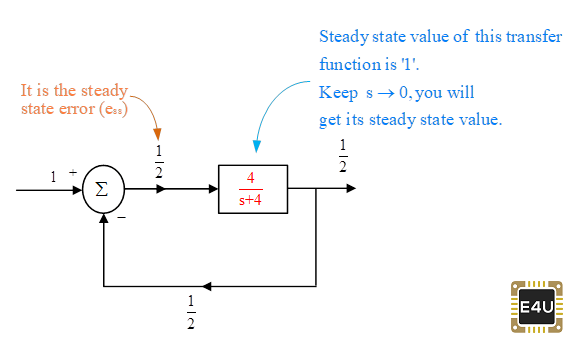
Se puede ver que el valor en estado estable de la señal de error es 0,5, por lo que el error en estado estable es 0,5. Si el sistema es estable y varias señales son constantes, entonces se pueden obtener varios valores de estado estacionario como sigue:

En la función de transferencia como …obtendrás la ganancia de estado estable de la función de transferencia.

Puede calcular la salida de la siguiente manera:

Recordando que = unidad de entrada de paso = podemos reorganizar esto:

El valor de estado estacionario de la salida es:

Podemos usar el método anterior para calcular el valor de estado estacionario de cualquier señal. Por ejemplo:

La entrada es (La entrada es la entrada de paso de unidad)

Su valor de estado estacionario = = 1.

De manera similar, la señal de error puede ser calculada como:

El valor de estado estacionario de la señal de error (es decir, el error de estado estacionario) es:

Además, se puede ver en la Figura-4 que la diferencia entre la entrada y la salida es de 0,5. Por lo tanto, el error de estado estacionario es 0,5.

Otro método para calcular el error de estado estacionario es el siguiente:

Calcular el coeficiente de error de posición Kp = Encontrarás a Kp = 1, ess= . Encontrarás la misma respuesta.

Si la entrada es una entrada de paso, digamos (es una entrada de paso, pero no una entrada de paso de unidad), entonces el error de estado estacionario es ess=

Si la entrada es la entrada de la rampa de la unidad, entonces Calcular, Coeficiente de error de velocidad Kv= , ess=

Si la entrada es una unidad de entrada parabólica, entonces Calcular, Coeficiente de error de aceleración Ka=, ess= .

Con el análisis de Kp, Kv y Ka…puedes entender cómo el error de estado estacionario depende de la entrada.

El controlador PI y el error de estado estacionario

A Controlador PI (es decir, un controlador proporcional más el controlador integral) reduce el error de estado estacionario (ess), pero tiene un efecto negativo en la estabilidad.

Los controladores de PI tienen la ventaja de reducir el error de estado estacionario de un sistema, mientras que tienen la desventaja de reducir la estabilidad del sistema.

Un controlador PI reduce la estabilidad. Esto significa que la amortiguación disminuye; el sobreimpulso de pico y el tiempo de asentamiento aumenta debido al controlador PI; las raíces de la ecuación de características (polos de la función de transferencia en bucle cerrado) en el lado izquierdo se acercarán más al eje imaginario. El orden del sistema también aumenta debido al controlador PI, que tiende a reducir la estabilidad.

Considere dos ecuaciones de características, una es s3+ s2+ 3s+20=0, otro es s2+3s+20=0. Sólo por observación, podemos decir que el sistema relacionado con la primera ecuación tiene menor estabilidad en comparación con la segunda ecuación. Puedes verificarlo encontrando las raíces de la ecuación. Así, puedes entender que las ecuaciones de características de orden superior tienen menor estabilidad.

Ahora, añadiremos un controlador PI (controlador proporcional más integral) en el sistema-1 (Figura-3) y examinaremos los resultados. Después de insertar el controlador PI en el sistema-1, se muestran varios valores de estado estacionario en la Figura-5. Se puede ver que la salida es exactamente igual a la entrada de referencia. La ventaja del controlador PI es que minimiza el error de estado estacionario de manera que la salida trata de seguir la entrada de referencia.

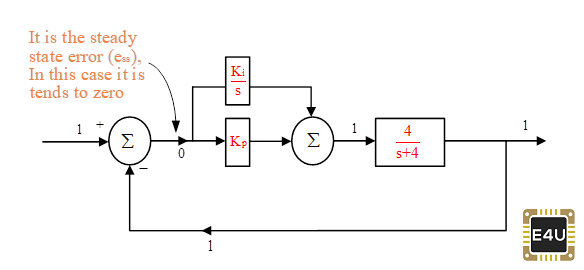
La función de transferencia del controlador PI puede calcularse como o Se puede preguntar que si la entrada de cualquier función de transferencia es cero, entonces su salida debería ser cero. Por lo tanto, en el presente caso la entrada del controlador PI es cero, pero la salida del controlador PI es un valor finito (es decir, 1). Esta explicación no se da en ningún libro de sistemas de control, por lo que la explicaremos aquí:

(1) El error de estado estacionario no es exactamente cero, tiende a cero, de manera similar s no es igual a cero, tiende a cero, de modo que en cualquier caso el error de estado estacionario es 2×10-3al mismo tiempo s (en particular estamos hablando de s en el denominador del controlador de PI) es también igual a 2×10-3por lo que la salida del controlador PI es 1.

Consideremos otro sistema de control que se muestra en la figura 6:

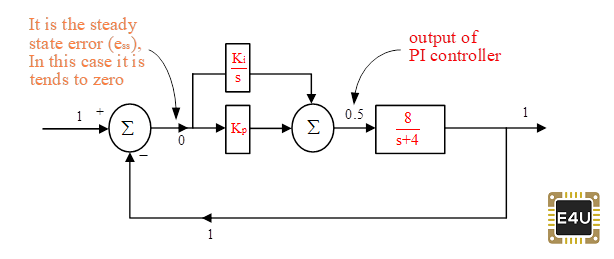
En este caso, podemos decir, en cualquier caso supongamos, que el error de estado estacionario es 2×10-3al mismo tiempo s es igual a 410-3; por lo tanto la salida del controlador PI es 0.5. Esto significa que tanto s como ess tienden a cero, pero su proporción es un valor finito.

En los libros del sistema de control nunca encontrarás s=0 o t=; siempre encontrarás

(2) La segunda explicación es que el error de estado estacionario es cero, s es también cero en estado estacionario. La función de transferencia del controlador PI es . En los libros de matemáticas, encontrarás que Th
no está definido, por lo que puede ser cualquier valor finito (véase la figura 7).

(3) La tercera explicación es, es un integrador. La entrada es cero, la integración de cero no está definida. Por lo tanto, la salida del controlador PI puede ser cualquier valor finito.

Una diferencia básica entre el sistema de control de bucle abierto y el sistema de control de bucle cerrado

En referencia a la explicación anterior, explicaremos una diferencia básica entre el sistema de control de bucle abierto y el sistema de control de bucle cerrado. Diferencias en el sistema de control de bucle abierto y en el sistema de control de bucle cerrado, las puede encontrar en cualquier libro de sistema de control*, pero una diferencia básica que está relacionada con la explicación anterior se da aquí y esperamos que ciertamente sea útil para los lectores.

Un sistema de control de bucle abierto puede representarse de la siguiente manera:

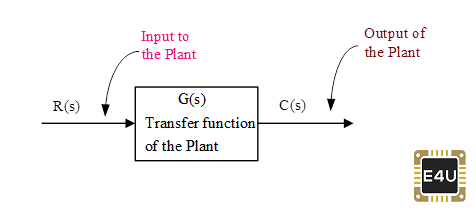
Un sistema de control de circuito cerrado (sistema de control de retroalimentación) puede representarse de la siguiente manera:

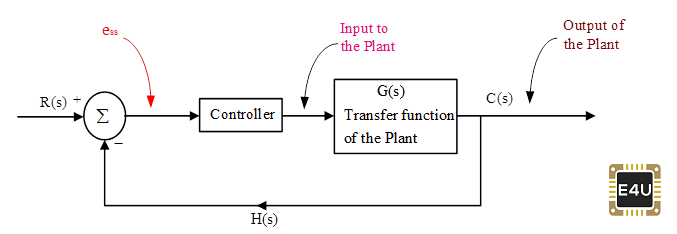
La función de transferencia de la planta es fija (la función de transferencia de la planta puede ser cambiada automáticamente debido a cambios ambientales, perturbaciones, etc.). En toda nuestra discusión, hemos asumido H(s)=1; Un operador puede controlar la función de transferencia del controlador (es decir, un parámetro del controlador tal que Kp, Kd, Ki) etc.

El controlador puede ser un controlador proporcional (controlador P), un controlador PI, un controlador PD, Controlador PID, Controlador de lógica difusa, etc. El controlador tiene dos objetivos: i) Mantener la estabilidad, es decir, la amortiguación debe ser de alrededor de 0,7-0,9, el sobreimpulso de pico y el tiempo de asentamiento debe ser bajo. ii) El error de estado estable debe ser mínimo (debe ser cero). Pero si intentamos aumentar la amortiguación, el error de estado constante puede aumentar. Por lo tanto, el diseño del controlador debe ser tal que ambos (estabilidad y error de estado estacionario) deben estar bajo control. El diseño óptimo del controlador es un vasto tema de investigación.

Está escrito antes, el controlador PI reduce el error de estado estacionario (ess) drásticamente, pero tienen un efecto negativo en la estabilidad.

Ahora, explicaremos una diferencia básica entre el sistema de control de bucle abierto y el sistema de control de bucle cerrado, que está relacionada con la explicación anterior.

Considere la figura 10; es un sistema de control de bucle abierto.

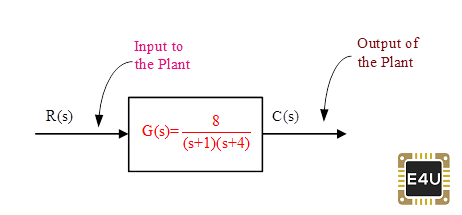
Let input es una entrada de paso de unidad. Por lo tanto, el valor de estado estacionario de la entrada es 1. Se puede calcular que el valor de estado estacionario de la salida es 2. Supongamos que hay un cambio en la función de transferencia [G(s)] de la planta debido a cualquier razón, ¿cuál será el efecto sobre la entrada y la salida? La respuesta es que la entrada de la planta no cambiará, la salida de la planta cambiará.

Consideremos ahora las figuras 11 y 12

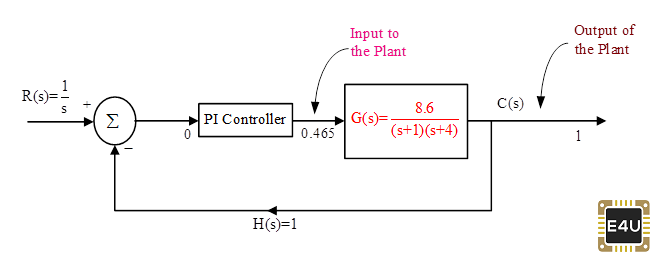
Ambos son sistemas de control de bucle cerrado. En la figura 11, supongamos que hay un cambio en la función de transferencia de la planta debido a cualquier razón, ¿cuál será el efecto sobre la entrada y la salida? En este caso, la entrada de la planta cambiará, la salida de la planta permanecerá sin cambios. La salida de la planta trata de seguir la entrada de referencia. La Figura -12 muestra las nuevas condiciones, en las que se cambian los parámetros de la planta. Se puede ver que la entrada de la planta se cambia a 0.476 desde 0.5, mientras que la salida no se cambia. En ambos casos la entrada al controlador PI es cero, las especificaciones del controlador PI son las mismas pero la salida del controlador PI es diferente.

Así que, puedes entender, en el sistema de control de bucle abierto se cambia la salida de la planta mientras que en el sistema de control de bucle cerrado se cambia la entrada a la planta.

En los libros del sistema de control, se puede encontrar la siguiente declaración:

En caso de variación de los parámetros de la función de transferencia de la planta, el sistema de control de bucle cerrado es menos sensible en comparación con el sistema de control de bucle abierto (es decir, la variación de la salida del sistema de control de bucle cerrado es menor en comparación con el sistema de control de bucle abierto).

Esperamos que la declaración anterior sea más clara con los ejemplos que se dan en este artículo.

___________________________________________________________________

*Queridos lectores de Electrical4U, tengan en cuenta que el propósito de este artículo no es reproducir los temas ya disponibles en los libros; pero nuestro objetivo es presentar varios temas complejos de Ingeniería de Control en un lenguaje fácil con ejemplos numéricos. Esperamos que este artículo le sea útil para comprender las diversas complejidades sobre los controladores de error en estado estacionario y de PI.