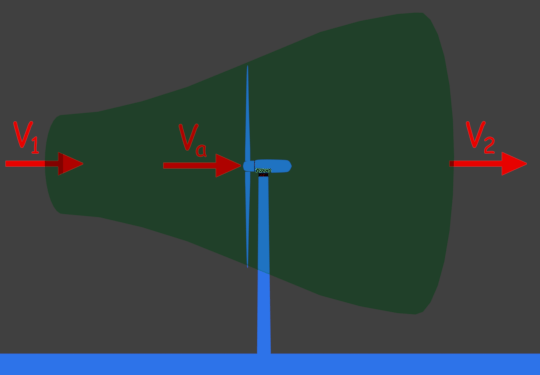
Para determinar la potencia extraída del viento por turbina de viento tenemos que asumir un conducto de aire como se muestra en la figura. También se supone que la velocidad del viento en la entrada del conducto es V1 y la velocidad del aire en la salida del conducto es V2. Digamos que la masa m de aire pasa por este conducto imaginario por segundo.
Ahora, debido a esta masa, la energía cinética del viento en la entrada del conducto es,![]()
![]()
De manera similar, debido a esta masa la energía cinética del viento en la salida del conducto es,![]()
![]()

Por lo tanto, la energía cinética del viento cambió, durante el flujo de esta cantidad de aire de la entrada a la salida del conducto imaginario es,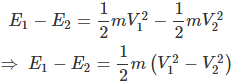
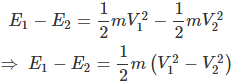
Como ya dijimos, la masa m de aire pasa por este conducto imaginario en un segundo. Por lo tanto, la energía extraída del viento es la misma que la energía cinética cambiada durante el flujo de masa m del aire desde la entrada a la salida del conducto.
Definimos la potencia como el cambio de energía por segundo. Por lo tanto, este poder extraído puede ser escrito como,![]()
![]()
Como la masa m del aire pasa en un segundo, nos referimos a la cantidad m como la tasa de flujo de masa del viento. Si pensamos en ello cuidadosamente, podemos entender fácilmente que la tasa de flujo de masa será la misma en la entrada, en la salida y también en cada sección transversal del conducto de aire. Ya que, cualquiera que sea la cantidad de aire que entra en el conducto, la misma sale por la salida.
Si VaA y son la velocidad del aire, el área de la sección transversal del conducto y la densidad del aire en las palas de la turbina respectivamente, entonces la tasa de flujo de masa del viento puede ser representada como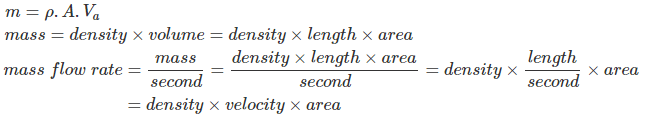
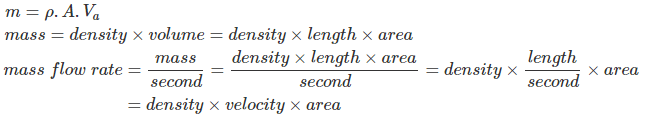
Ahora, sustituyendo m por VaA en la ecuación (1), tenemos,![]()
![]()
Ahora bien, como se supone que la turbina está situada en el centro del conducto, la velocidad del viento en las palas de la turbina puede considerarse como la velocidad media de las velocidades de entrada y salida.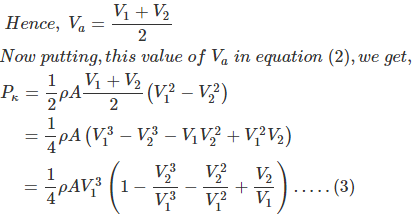
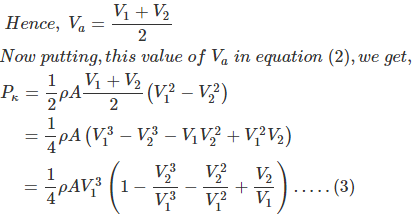
Para obtener la máxima potencia del viento, tenemos que diferenciar la ecuación (3) con respecto a V2 y la equipara a cero. Eso es,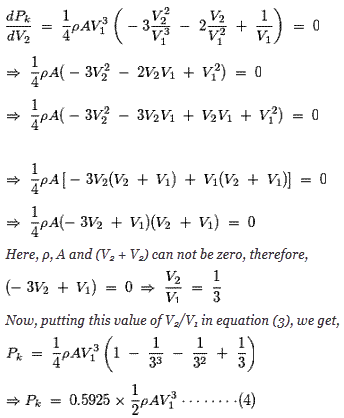
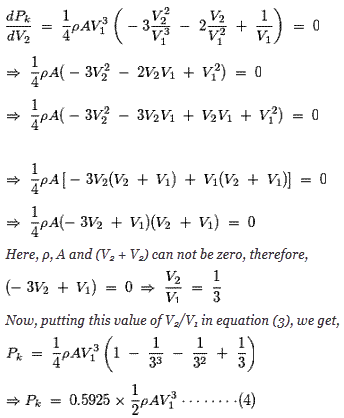
Coeficiente de Betz
De la ecuación anterior se desprende que la potencia máxima teórica extraída del viento se encuentra en la fracción de 0,5925 de su potencia cinética total. Esta fracción se conoce como la Coeficiente de Betz. Esta potencia calculada está de acuerdo con teoría de la turbina de viento pero la potencia mecánica real que recibe el generador es menor que eso y se debe a las pérdidas en los cojinetes del rotor de fricción y a las ineficiencias del diseño aerodinámico de la turbina.
De la ecuación (4) se desprende claramente que la potencia extraída es
- Directamente proporcional a la densidad del aire. A medida que la densidad del aire aumenta, la potencia de la turbina aumenta.
- Directamente proporcional al área de barrido de las palas de la turbina. Si la longitud de los álabes aumenta, el radio del área barrida aumenta en consecuencia, por lo que la potencia de la turbina aumenta.
- La potencia de la turbina también varía con la velocidad3 del viento. Eso indica que si la velocidad del viento se duplica y la potencia de la turbina aumenta a ocho veces.

