Antes de estudiar ingeniería eléctrica es esencial saber que la relación angular entre principalmente voltaje y actual en un sistema. Para entender la relación entre el voltaje y debemos saber primero definición de vector y pasar por álgebra vectorial y diagrama vectorial.
Definición de Vector
Hay algunas cantidades que tienen tanto magnitud como dirección de acción. Este tipo de cantidades se denomina cantidad vectorial. Así es como uno puede hacer que las cantidades básicas definición de vector en muy pocas palabras. El concepto más básico de un vector es que, es una representación de este tipo de cantidades tanto en magnitud como en dirección. Siempre que representamos cualquier cantidad puede tener alguna dirección de acción. Supongamos que si decimos, una fuerza de 5 N, no completa el cuadro.
Siempre debemos decir la fuerza en qué dirección, es decir, que la fuerza de 5 N está en la parte superior, inferior o en cualquier otra dirección. Así que la cantidad vectorial debe ser representada con la magnetita así como su dirección. La dirección de cualquier cantidad puede representarse midiendo el ángulo formado por la dirección de la cantidad y un eje de referencia.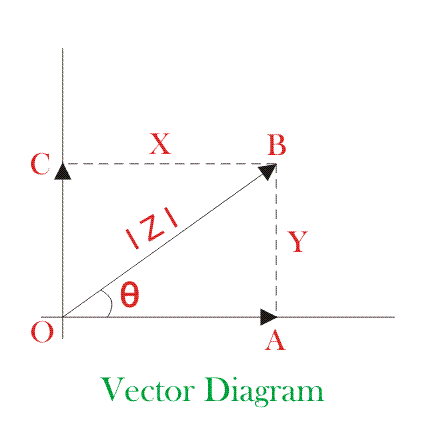

Aquí en este diagrama vectorial el vector OB tiene una magnitud de |Z| en un ángulo con el eje de referencia ox. Esto puede resolverse en dos componentes en ángulo recto entre sí, digamos que son 

El método convencional de representación del vector 

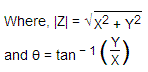
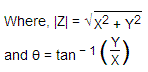
Álgebra vectorial
Ahora discutiremos sobre álgebra vectorial. Para una calibración diferente, el vector debe expresarse algebraicamente. En el diagrama vectorial el vector Z es el resultado de la suma vectorial de sus componentes X e Y.
Este vector puede estar escrito en álgebra vectorial como 

Donde, j indica que el componente Y está en perpendicular al componente X. El eje x en el diagrama vectorial se conoce como eje real o en fase y el eje vertical y se llama eje imaginario o de cuadratura. El símbolo j, que está asociado con la componente de cuadratura Y, puede considerarse como un operador que gira un vector en sentido contrario a las agujas del reloj a través de 90o. Si un vector tiene que ser rotado en sentido contrario a las agujas del reloj a través de 180o entonces el operador j tiene que realizar su función dos veces y como el vector ha invertido su sentido entonces j.j o j2 = − 1
| Lo que implica, j = | − 1 |
Así que hemos visto que una cantidad vectorial puede ser representada de diferentes formas,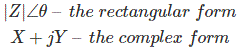
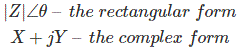
Relación entre la forma rectangular y la forma compleja de un vector
Según el diagrama vectorial que se muestra en esta página. La magnitud del vector Z es![]()
![]()
De estas dos ecuaciones, obtenemos,

Poniendo estos valores de X e Y, en forma compleja de Z, obtenemos,

El valor de la expresión anterior se conoce como forma trigonométrica del vector. De nuevo sabemos que, cos y sin pueden ser representados en forma exponencial de la siguiente manera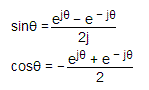
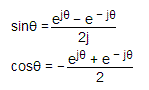
Si ponemos esto sobre la forma exponencial de pecado y cos en la ecuación Z = |Z|(cos + jsin) obtenemos,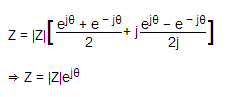
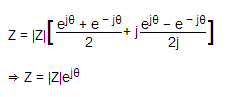
Z = |Z|ej
Esta es la forma exponencial del vector.
Por lo tanto, de todas las expresiones anteriores de álgebra vectorial y diagramas vectorialespuede concluirse que una cantidad vectorial puede representarse como un total de cuatro formas básicas que se enumeran a continuación
