Cuando un voltaje se aplica repentinamente a través de un condensadorque no están previamente cargados, los electrones que cambian de fuente a condensador a fuente comienzan inmediatamente. En otras palabras, la acumulación del cambio en el condensador comienza instantáneamente. A medida que la carga que se acumula en el condensador aumenta, el voltaje desarrollado a través del condensador aumenta. El voltaje desarrollado a través del condensador se aproxima al voltaje de suministro, la tasa de acumulación de carga en el condensador disminuye en consecuencia. Cuando estos dos voltajes se igualan entre sí, ya no habrá más flujo de carga de la fuente al condensador. Los flujos de electrones de la fuente al condensador y el condensador a la fuente no son más que La corriente eléctrica.
Al principio, esta corriente será máxima y después de cierto tiempo la corriente será cero. La duración en la que la corriente cambia en el condensador se conoce como período transitorio. El fenómeno de la corriente de carga u otras cantidades eléctricas como el voltaje, en el condensador se conoce como transitorio.
Para entender el comportamiento transitorio del condensador dibujemos un circuito RC como se muestra a continuación,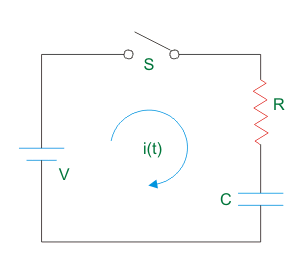

Ahora, si el interruptor S se cierra de repente, la corriente comienza a fluir a través del circuito. Vamos a actual en cualquier momento es i(t).
También considere el voltaje desarrollado en el condensador en ese instante es Vc(t).
Por lo tanto, al aplicar Ley de tensión de Kirchhoffsen ese circuito que tenemos,
Ahora bien, si la transferencia de carga durante este período (t) es q culombio, entonces i(t) puede ser escrito como![]()
![]()
Por lo tanto,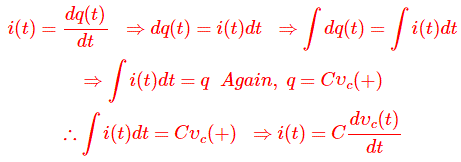
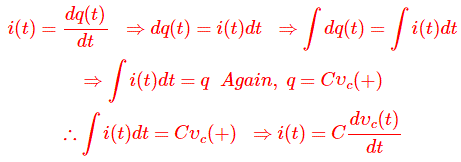
Poniendo esta expresión de i(t) en la ecuación (i) obtenemos,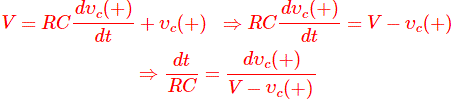
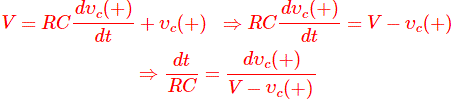
Ahora integrando ambos lados con respecto al tiempo que tenemos,![]()
![]()
Donde, K es una constante puede ser determinada desde la condición inicial.
Consideremos el tiempo t = 0 en el instante de encender el circuito poniendo t = 0 en la ecuación anterior que obtenemos,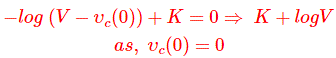
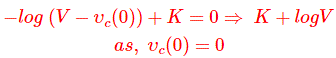
No se desarrollará ningún voltaje a través de condensador en t = 0 como antes no había cambiado.
Por lo tanto,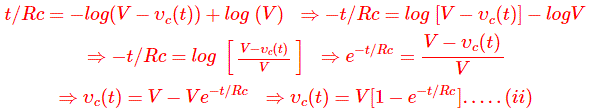
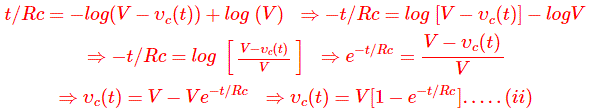
Ahora si ponemos RC = t en la ecuación anterior, obtenemos
Este RC o producto de resistencia y capacitancia del circuito de la serie RC se conoce como la constante de tiempo del circuito. Así, la constante de tiempo de un circuito RC, es el tiempo durante el cual el voltaje desarrollado o caído a través del condensador es 63,2% del voltaje de suministro. Esta definición de constante de tiempo sólo es válida cuando el condensador no ha sido modificado inicialmente.
De nuevo, en el momento de encender el circuito, es decir, t = 0, no se desarrollará ningún voltaje a través del condensador. Esto también puede demostrarse a partir de la ecuación (ii).
Así que la corriente inicial a través del circuito es, V/R y considerémoslo como I0.
Ahora, en cualquier momento, actual a través del circuito será,![]()
![]()
Ahora cuando, t = Rc la corriente del circuito.
Así que en el instante en que, la corriente a través de la condensador es el 36,7% de la corriente inicial, también se conoce como constante de tiempo del circuito RC.
La constante de tiempo normalmente se denota voluntad (taw). Por lo tanto,
Transitorio durante la descarga de un condensador
Ahora, supongamos que el condensador está completamente cargado, es decir, el voltaje en el condensador es igual al voltaje de la fuente. Ahora bien, si el fuente de tensión está desconectado y en su lugar dos terminales de la batería están en cortocircuito, el condensador se estrella descargando medios, la distribución desigual de electrones entre dos placas se igualará a través del camino del cortocircuito. El proceso de igualar la concentración de electrones en dos placas continuará hasta que el voltaje en el condensador sea cero. Este proceso se conoce como descarga de condensador. Ahora examinaremos el el comportamiento transitorio del condensador durante la descarga.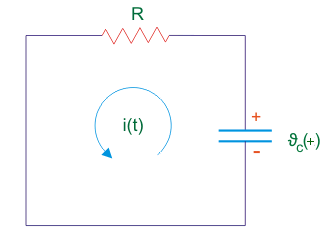

Ahora, desde el circuito anterior aplicando Ley actual de Kirchhoff…que tenemos,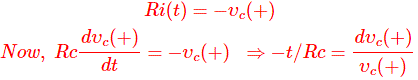
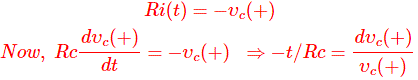
Integrando ambos lados conseguimos,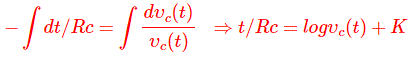
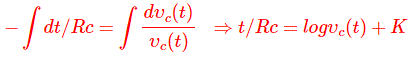
K es la constante que se puede determinar a partir del valor inicial. Ahora, en el momento del cortocircuito del condensador,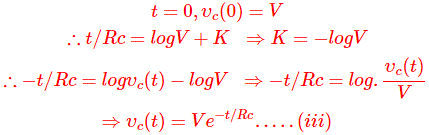
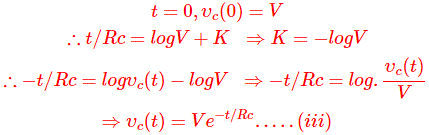
Ahora, de la ecuación (iii), aplicando t = = RC obtenemos,
De nuevo, la corriente del circuito en ese momento es = RC,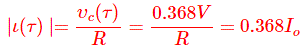
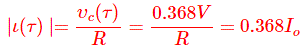
Así, en la constante de tiempo del condensador, ambos condensador …el voltaje,c y actual se reducen al 36,8% de su valor inicial.





