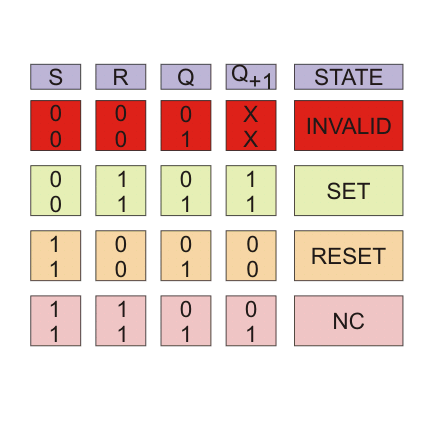
El tipo más simple de chancla es S R Flip Flop. Tiene dos entradas S y R y dos salidas Q y 
. El estado de este pestillo está determinado por la condición de Q. Si Q es 1, se dice que el pestillo está fijado y si Q es 0, se dice que el pestillo está reajustado. Este S R Latch o la chancla puede ser diseñada ya sea por dos acoplamientos cruzados Puertas NAND o dos cruces acoplados… Puertas NOR. Cuando diseñemos este pestillo usando las puertas NOR, será un pestillo S-R alto activo. Eso significa que está fijado cuando S = 1. Cuando diseñamos este cierre usando puertas NAND, será un cierre activo de S-R bajo. Eso significa que está fijado cuando S = 0. S R Flip Flop también se llama SET RESET Flip Flop.
La figura de abajo muestra el circuito lógico de Cierre S R.
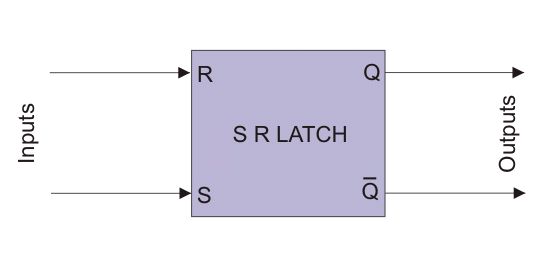
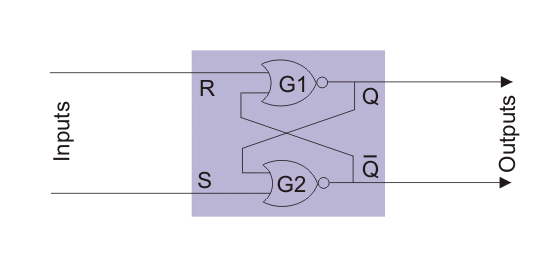
En el circuito lógico anterior, si S = 1 y R = 0, Q se convierte en 1. Expliquemos cómo.
- La puerta NOR siempre da la salida 0 cuando al menos una de las entradas es 1.
- Así que cuando S se aplica como 1 la salida de la puerta G2, es decir es 0 independientemente de la condición de la segunda entrada Q a la puerta.
- Ahora es la entrada de la puerta G1, así que ambas entradas de G1 se convierten en 0, ya que R ya es 0. Por lo tanto, la salida de G1 es ahora
o 1. - Así que cualquiera que sea la condición previa de Q, siempre se convierte en Q = 1 y = 0 cuando, S = 1 y R = 0. Esto se llama condición SET del pestillo.
En el circuito lógico anterior, si S = 0 y R = 1, Q se convierte en 0. Expliquemos cómo.
- Como ya dijimos, una puerta NOR siempre da la salida 0 cuando al menos una de las entradas es 1.
- Así que cuando R se aplica como 1, la salida de la puerta G1, es decir, Q, es 0 independientemente de la condición de la segunda entrada a la puerta.
- Así que, cualquiera que sea la condición previa de Q, siempre se convierte en 0 este 0 se retroalimenta a la entrada de la puerta G2. Como aquí S ya es 0, ambas entradas de G2 son 0. Por lo tanto, la salida de G2, es decir será 1. Así que, Q = 0 y = 1 cuando, S = 0 y R = 1. Esto se llama condición de RESET del pestillo.
En el circuito lógico anterior, si S = 0 y también R = 0, Q permanece igual que antes. Expliquemos cómo.
- Primero supongamos que Q es previamente 1.
- Ahora las entradas de G2 son 0 y 1 como S=0 y Q=1. Así que la salida de G2, es decir es
o 0. - Ahora ambas entradas de G1 son 0 como R=0 y =0. Así que la salida de G1, es decir, Q es o 1.
- Ahora supongamos que Q es previamente 0.
- Ahora ambas entradas de G2 son 0 y 1 como S = 0 y Q = 0. Así que la salida de G2, es decir. es o 1.
- Ahora las entradas de G1 son 0 y 1 como R=0 y = 1. Así que la salida de G1, es decir, Q es o 0.
- Así que está probado que Q permanece igual que cuando S = 0 y también R = 0 en el cierre de S R o chancla.
En el circuito lógico anterior, si S = 1 y también R = 1, la condición de Q es totalmente impredecible. Expliquemos cómo.
- Primero supongamos que Q es previamente 1.
- Ahora ambas entradas de G2 son 1 como S = 1 y Q = 1. Así que la salida de G2, es decir es
o 0. - Ahora las entradas de G1 son 1 y 0 como R = 1 y = 0. Así que la salida de G1, es decir, Q es
o 0. Eso significa que la Q está cambiada. - Ahora Q es 0. Así que las entradas de G2 son 1 y 0 como S = 1 y Q = 0. Así que la salida de G2, es decir. es o 0. Eso significa no ha cambiado.
- Ahora las entradas de G1 son 1 y 0 como R = 1 y = 0. Así que la salida de G1, es decir, Q es o 0. Eso significa que Q no ha cambiado.
Así que, cuando tanto S como R son 1, se vuelve impredecible si el valor de la salida Q se cambiará o no. Esta condición de bloqueo de S R normalmente se evita. Como el seguro está fijado cuando S = 1(ALTO), el seguro se llama Seguro S R activo alto. Hay otro tipo de cierre que está AJUSTADO cuando, S = 0 (BAJO), y este cierre se conoce como Cierre activo de baja S R.
