Todos sabemos que hay contadores que pasan a través de un número definido de estados en un orden predeterminado. Por ejemplo, un contador ascendente de 3 bits cuenta de 0 a 7 mientras que el mismo orden se invierte en el caso del contador descendente de 3 bits. Estos circuitos, cuando se manipulan adecuadamente, pueden hacerse contar hasta un nivel intermedio también. Esto significa que en lugar de contar hasta 7, podemos terminar el proceso poniendo a cero el contador justo en, digamos, 5. Tales contadores se conocen entonces como contadores mod-N. Sin embargo, incluso en este caso, el orden en el que cuentan no se alterará. Pero, ¿y si necesitamos a través de un patrón específico que no se adhiere a esta forma estándar de contar? La solución sería diseñar un generador de secuencias.
Esto se debe a que los generadores de secuencias no son más que un conjunto de circuitos digitales diseñados para producir una secuencia de bits específica a su salida. Hay varias maneras en las que estos circuitos pueden ser diseñados, incluyendo aquellos que están basados en multiplexores y chanclas. Aquí en este artículo nos ocupamos del diseño del generador de secuencias usando Chancletas D (por favor, tenga en cuenta que incluso Chancletas JK se puede utilizar).
Como ejemplo, consideremos que pretendemos diseñar un circuito que se mueva a través de los estados 0-1-3-2 antes de repetir el mismo patrón. Los pasos involucrados durante este proceso son los siguientes.
Paso 1
En primer lugar, tenemos que determinar el número de chanclas que se necesitarían para lograr nuestro objetivo. En nuestro ejemplo, hay 4 estados que son idénticos a los estados de un contador de 2 bits, excepto el orden en que transitan. A partir de esto, podemos adivinar que el requisito de las chancletas es de 2 para lograr nuestro objetivo.
Paso 2
Teniendo esto en cuenta, escribamos ahora la tabla de transición de estado para nuestro generador de secuencias. Esto se muestra en las cuatro primeras columnas de la Tabla I en las que las dos primeras columnas indican los estados actuales mientras que las dos siguientes indican los correspondientes estados siguientes. Por ejemplo, el primer estado en nuestro ejemplo es 0 = 00 que lleva al siguiente estado 1 = 01 (como se muestra en la fila sombreada en gris de la Tabla I).
Paso 3
Ahora esta tabla de transición de estados se ampliará para incluir la tabla de excitación de la flip-flop con el que deseamos diseñar nuestro circuito. En nuestro caso, no es más que D flip-flop por lo que tenemos la quinta y sexta columna de la tabla que representa la tabla de excitación de la chancleta D.
Por ejemplo, miren la fila sombreada en naranja de la Tabla I en la que los estados actual y siguiente 1 y 0 (respectivamente) dan como resultado D1 para ser 0. La misma fila también muestra el caso en el que
Tabla I
| Estados actuales | Próximos Estados | Entradas de chancletas D | |||
| Q1 | Q0 | Q1+ | Q0+ | D1 | D0 |
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
Paso 4
Ahora es el momento de derivar las expresiones booleanas para D1 y D0. Esto se puede hacer usando cualquier tipo de técnica de simplificación, incluyendo K-map. Sin embargo, como nuestro ejemplo es bastante simple, podemos usar el Las leyes de Boole para resolver para D1 y D0. Así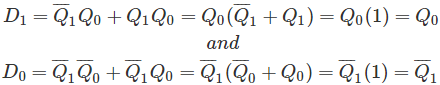
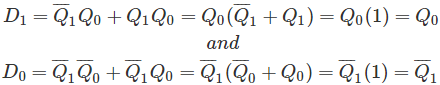
Paso 5
Habiendo conocido las entradas de cualquiera de los Chancletas Dahora podemos diseñar nuestro generador de secuencias como se muestra en esta figura.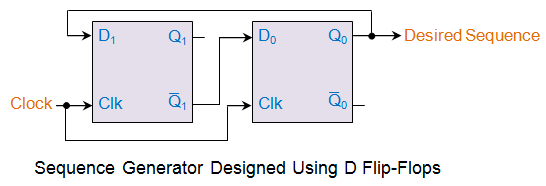

En el circuito mostrado, la secuencia deseada se genera en base a los pulsos de reloj suministrados. En este punto, cabe señalar que, la analogía presentada aquí para un diseño simple puede extenderse efectivamente para generar una secuencia más larga de bits.
