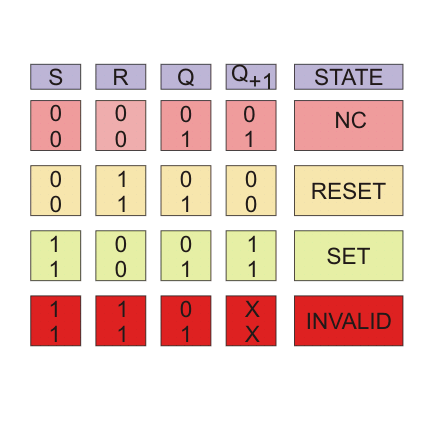
Hay un tipo de cierre que se fija cuando S = 0 (BAJA), y este cierre se conoce como Activo Bajo S R LatchEste cierre está normalmente diseñado usando Puertas NAND. El circuito lógico se muestra a continuación.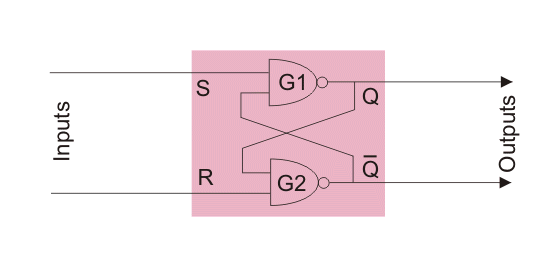
En el circuito lógico anterior, si S = 0 y R = 1, Q se convierte en 1. Expliquemos cómo.
- La puerta NAND siempre da la salida 1 cuando al menos una de las entradas es 0.
- Así, cuando S se aplica como 0 la salida de la puerta G1, es decir, Q es 1 independientemente de la condición de la segunda entrada
a la puerta. - Ahora, Q es la entrada de la puerta G2, así que ambas entradas de G2 se convierten en 1, ya que R ya es 1. Así que la salida de G2 es ahora
o 0. - Así que cualquiera que sea la condición previa de Q, siempre se convierte en Q = 1 y = 0 cuando S = 0 y R = 1. Esto se llama condición SET del pestillo.
En el circuito lógico anterior, si S = 1 y R = 0, Q se convierte en 0. Expliquemos cómo.
- Como ya dijimos, una puerta NAND siempre da la salida 1 cuando al menos una de las entradas es 0.
- Así que cuando R se aplica como 0, la salida de la puerta G2, es decir. es 1, independientemente de la condición de la segunda entrada Q a la puerta.
- Así que cualquiera que sea la condición previa de …siempre se convierte en 1, este 1 se retroalimenta a la entrada de la puerta G1. Como aquí S ya es 1, ambas entradas de G1 son 1. Por lo tanto, la salida de G1, es decir, Q será 0. Así que Q = 0 y = 1 cuando, S = 1 y R = 0. Esto se llama condición de RESET del pestillo.
En el circuito lógico anterior, si S = 1 y también R = 1, Q permanece igual que antes. Expliquemos cómo.
- Primero supongamos que Q es previamente 1.
- Ahora ambas entradas de G2 son 1 como R = 1 y Q = 1. Así que la salida de G2, es decir es o 0.
- Ahora las entradas de G1 son 1 y 0 como R = 1 y = 0. Así que la salida de G1, es decir, Q es
o 1. - Ahora supongamos que Q es previamente 0.
- Ahora las entradas de G2 son 1 y 0 como R = 1 y Q = 0. Así que la salida de G2, es decir. es o 1.
- Ahora ambas entradas de G1 son 1 como S = 1 y = 1. Así que la salida de G1, es decir, Q es o 0.
- Así que está probado que Q sigue siendo el mismo cuando, S = 1 y también R = 1.
En el circuito lógico anterior, si S = 0 y también R = 0, la condición de Q es totalmente impredecible. Expliquemos cómo.
- Primero supongamos que Q es previamente 0.
- Ahora ambas entradas de G2 son 0 como R = 0 y Q = 0. Así que la salida de G2, es decir. es
o 1. - Ahora las entradas de G1 son 0 y 1 como S=0 y = 1. Así que la salida de G1, es decir, Q es
o 1. Eso significa que la Q está cambiada. - Ahora Q es 1. Así que las entradas de G2 son 0 y 1 como R = 0 y Q = 1. Así que la salida de G2, es decir es o 1. Eso significa que no ha cambiado.
- Ahora las entradas de G1 son 0 y 1 como S=0 y = 1. Así que la salida de G1, es decir, Q es o 1. Eso significa que Q no ha cambiado.
Así que, cuando tanto S como R son 0, se vuelve impredecible si el valor de la salida Q será cambiado o no. Esta condición de Cierre S R Normalmente se evita.
