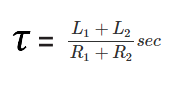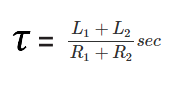Tomemos, un simple circuito RC como se muestra a continuación.
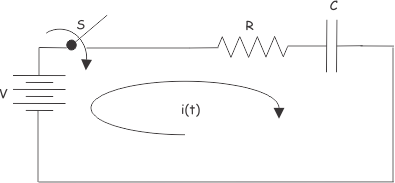

Asumamos que el condensador no se modifica inicialmente y el interruptor S se cierra en el momento t = 0. Después de cerrar el interruptor, La corriente eléctrica comienza a fluir a través del circuito. Aplicando Ley de tensión de Kirchhoff en que un circuito de malla única…que tenemos,
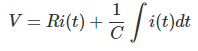
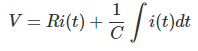
Diferenciando ambos lados con respecto al tiempo t, obtenemos,
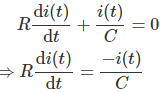
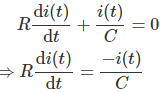
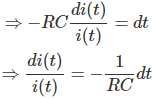
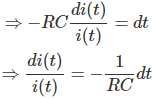
Integrando ambos lados conseguimos,
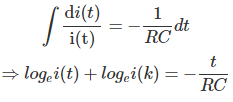
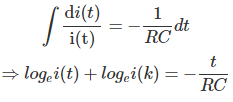
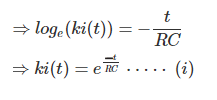
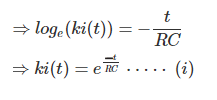
Ahora, en t = 0, el condensador se comporta como un cortocircuito, así que, justo después de cerrar el interruptor, la corriente a través del circuito será,
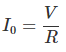
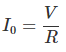
Ahora, poniendo este valor en la ecuación (i) obtenemos,
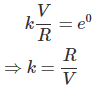
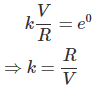
Poniendo el valor de k en la ecuación (i) obtenemos,
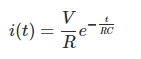
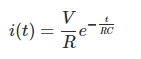
Ahora, si ponemos t = RC en la expresión final de la corriente del circuito i(t), obtenemos,
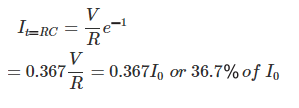
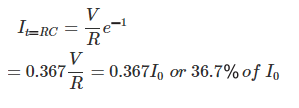
De la expresión matemática anterior queda claro que RC es el tiempo en segundo durante el cual la corriente en un condensador de carga disminuye al 36,7 por ciento de su valor inicial. El valor inicial significa que la corriente en el momento de encender el condensador.
Este término es bastante significativo para analizar el comportamiento de los circuitos capacitivos e inductivos. Este término se conoce como constante de tiempo. Así que constante de tiempo es la duración en segundos durante la cual la corriente a través de un circuito de capacidades se convierte en el 36,7 por ciento de su valor inicial. Esto es numéricamente igual al producto de la resistencia y el valor de la capacidad del circuito. La constante de tiempo normalmente se denota con (tau). Así que..,
En un complejo circuito RC, constante de tiempo será producto de la resistencia y capacitancia equivalente del circuito.
Discutamos el significado de la constante de tiempo con más detalles para eso, trazaremos la corriente i(t).
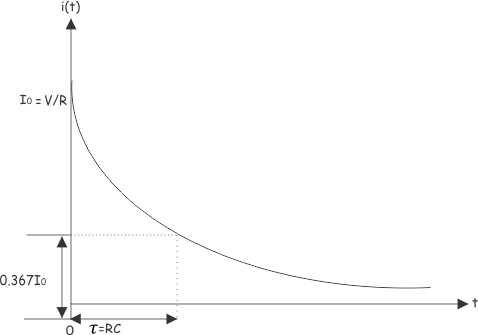

En t = 0, la corriente a través de la condensador El circuito es
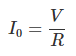
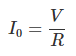
En t = RC, la corriente a través de la condensador es
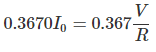
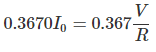
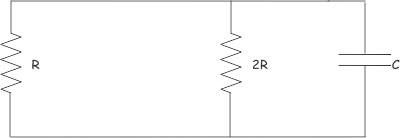
Consideremos, otro circuito RC.
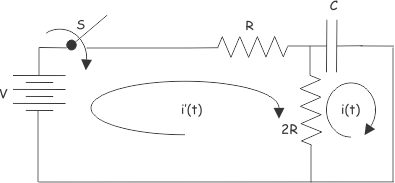

Ecuaciones de circuitos usando KVL de los circuitos anteriores son,
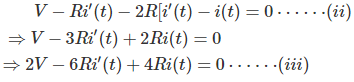
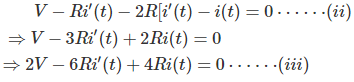
y
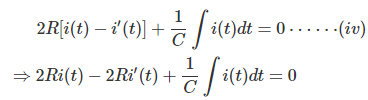
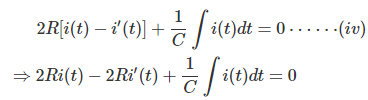
![]()
![]()
De los apartados iii) y v)
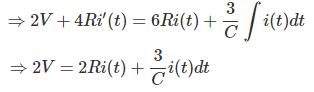
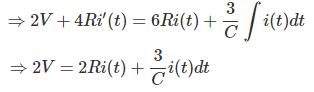
Diferenciando ambos lados con respecto al tiempo t, conseguimos,
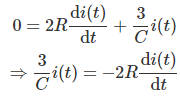
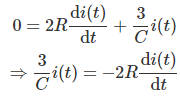
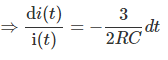
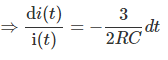
Integrando ambos lados conseguimos,
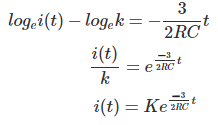
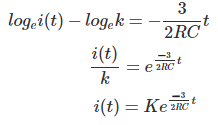
En t = 0,
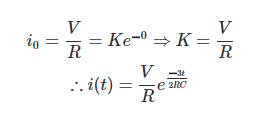
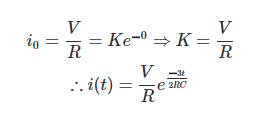
La constante de tiempo de este circuito sería 2RC/3 seg. Ahora, la resistencia equivalente del circuito es,

![]()
![]()
La constante de tiempo del circuito se ha convertido
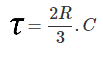
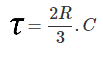
![]()
![]()
Consideremos un ejemplo de circuito RL en serie
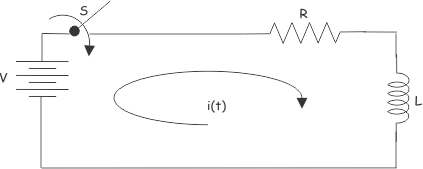

Aplicando Ley de tensión de Kirchhoff en el circuito de arriba. Lo conseguimos,
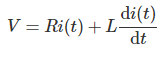
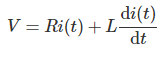
La ecuación también puede ser resuelta Transformación de Laplace técnica. Para eso tenemos que tomar Transformación de Laplace de la ecuación en ambos lados,
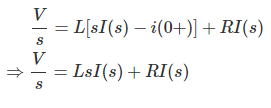
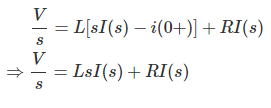
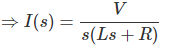
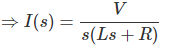
Por lo tanto, en esta ecuación.
![]()
![]()
Ya que, la corriente justo después de que se encienda el interruptor, la corriente a través de la inductor será cero.
Ahora,
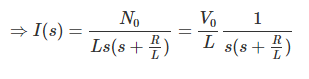
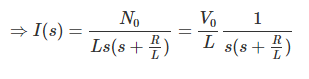
Tomando el Laplace inverso de la ecuación anterior, obtenemos,
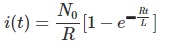
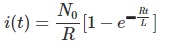
Ahora, si ponemos,
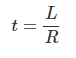
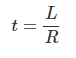
Lo conseguimos,
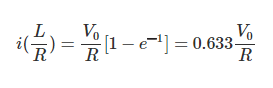
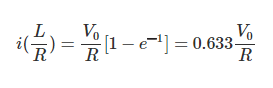
Así que, en el circuito RL, en el tiempo = L/R seg. la corriente se convierte en el 63,3% de su valor final en estado estable. El L/R se conoce como la constante de tiempo de un Circuito LR. Trazamos la corriente de inductor circuito.
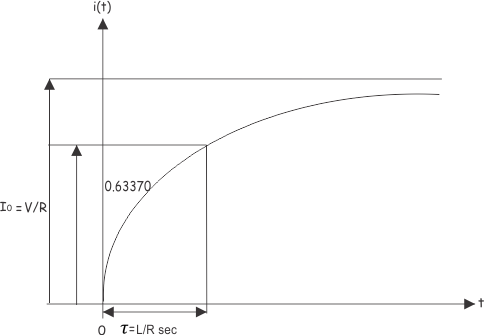

La constante de tiempo de un Circuito LR es la relación entre la inductancia y la resistencia del circuito. Tomemos otra 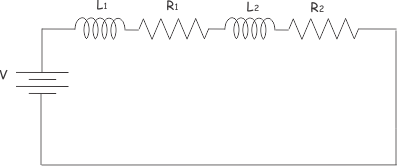

Este circuito puede ser redibujado como,
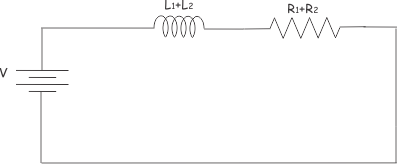

Así que, la constante de tiempo del circuito sería