Circuito RLC en serie

Cuando resistencia, inductor y condensador están conectados en serie a través de un voltaje el circuito así obtenido se llama circuito RLC en serie.

El diagrama de fases del circuito RLC en serie

El diagrama de fases del circuito RLC en serie se dibuja combinando el diagrama de fases de la resistencia, el inductor y el condensador. Antes de hacerlo, uno debe entender la relación entre el voltaje y actual en el caso de la resistencia, el condensador y el inductor.

1. 1. 1. Resistencia
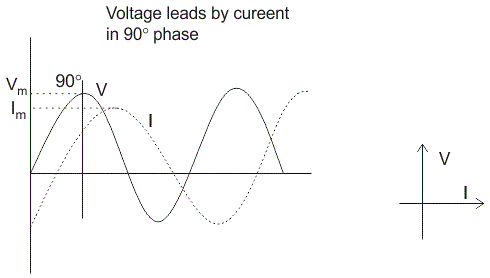
         En el caso de la resistencia, el voltaje y la corriente están en la misma fase o podemos decir que la diferencia de ángulo de fase entre el voltaje y la corriente es cero.
      2. Inductor
         En el inductor, el voltaje y la corriente no están en fase. El voltaje lleva al de la corriente en 90 o, en otras palabras, el voltaje alcanza su máximo y el valor cero 90 antes de que la corriente lo alcance.
      3. Condensador
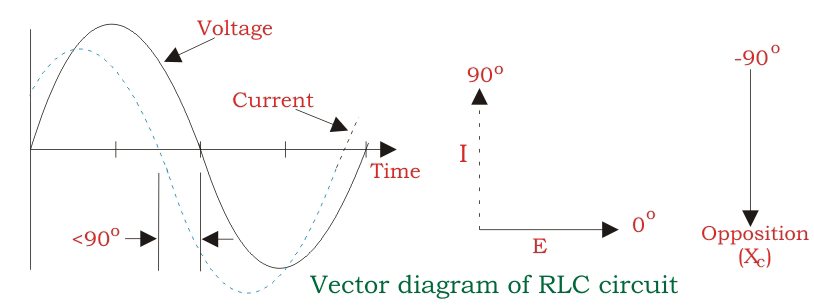
         En el caso del condensador, la corriente conduce la tensión en 90 o, en otras palabras, la tensión alcanza su máximo y el valor cero 0 después de que la corriente la alcanza, es decir, el diagrama de fases del condensador es exactamente opuesto al del inductor.

NOTA: Para recordar la relación de fase entre el voltaje y la corriente, aprenda esta simple palabra llamada CIVIL, es decir, en la corriente del condensador conduce el voltaje y el voltaje conduce la corriente en el inductor.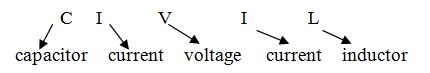

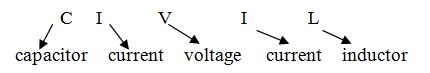
Circuito RLC
Para dibujar el diagrama de fases del circuito RLC en serie, siga estos pasos:

Paso I. En el caso de un circuito RLC en serie, la resistencia, el condensador y el inductor están conectados en serie, por lo que la corriente que fluye en todos los elementos es la misma, es decir, I r = Il = Ic = I. Para dibujar el diagrama de los fáseres, tome el fásor actual como referencia y dibújelo en el eje horizontal como se muestra en el diagrama.
Paso II. En el caso de la resistencia, tanto el voltaje como la corriente están en la misma fase. Así que dibuja el fásor del voltaje, VR a lo largo del mismo eje o dirección que el del fásor actual, es decir, VR está en fase con I.
Paso III. Sabemos que en el inductor, el voltaje lleva la corriente a 90, así que saca Vl (caída de voltaje a través del inductor) perpendicular al fásor de la corriente en la dirección de avance.
Paso IV. En el caso del condensador, el voltaje se retrasa con respecto a la corriente en 90, por lo que se consume Vc (caída de voltaje a través del condensador) perpendicular al fasor de la corriente en dirección descendente.
Paso V. Para dibujar el diagrama resultante, dibuje Vc en dirección ascendente. Ahora dibuja la resultante, Vs que es la suma vectorial del voltaje Vr y VL VC.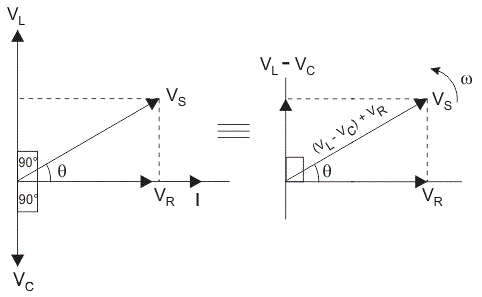

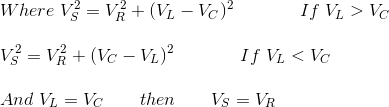
Impedancia para un circuito RLC en serie

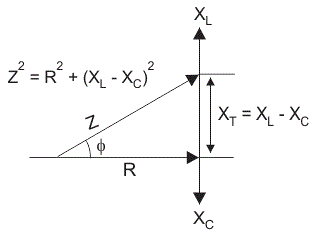
La impedancia Z de un circuito RLC en serie se define como la oposición al flujo de corriente, debido a la resistencia del circuito R, la reactancia inductiva, XL y la reactancia capacitiva, XC. Si la reactancia inductiva es mayor que la capacitiva, es decir, XL > XCentonces el circuito RLC tiene un ángulo de fase retardado y si la reactancia capacitiva es mayor que la inductiva, es decir XC > XL entonces el circuito RLC tiene el ángulo de fase principal y si tanto el inductivo como el capacitivo son iguales, es decir, XL = XC entonces el circuito se comportará como un circuito puramente resistivo.

Ya lo sabemos,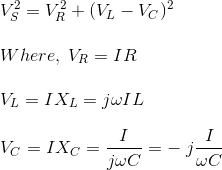

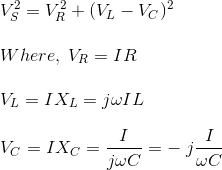
Sustituyendo los valores VS2 = (IR)2 + (I XL I XC )2

A partir de este triángulo de impedancia: usando el teorema de Pitágoras obtenemos;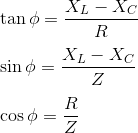

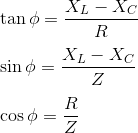
Variación de la resistencia, la reactancia y la impedancia con la frecuencia

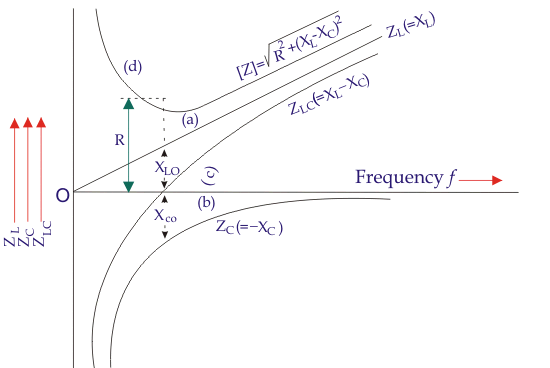
En el circuito RLC en serie, hay tres tipos de impedancia involucrados…

1. Resistencia eléctrica La resistencia es independiente de la frecuencia, por lo que se mantiene constante con el cambio de frecuencia.
2. Reactancia inductiva, XL – Sabemos que XL = 2fL. Por lo tanto, la reactancia inductiva varía directamente con la frecuencia. Así que el gráfico entre la frecuencia y la reactancia inductiva es una línea recta que pasa por el centro como muestra la curva a.
3. Reactancia capacitiva, XC – De la fórmula de la reactancia capacitiva, XC = 1/ 2fC por lo que la reactancia capacitiva varía inversamente con la frecuencia. Dado que la reactancia neta es ( XL XC). Así que para dibujar la curva de ( XL XC), primero dibuja el gráfico de ( -XC) que se muestra por la curva b y luego dibujar una curva para la reactancia neta que se muestra como curva c.
4. La impedancia total del circuito se muestra por la curva d que se obtiene añadiendo un valor de resistencia constante a la reactancia neta.