Circuito de la serie RL

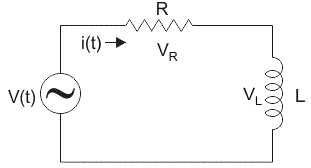
Considere un simple circuito RL en el que resistenciaR e inductor, L están conectados en serie con un voltaje suministro de voltios V. Pensemos que el actual que fluye en el circuito es I (amperio) y la corriente a través de la resistencia y inductor es que yoR y yoL respectivamente. Ya que ambos resistencia y el inductor están conectados en serie, por lo que la corriente tanto en los elementos como en el circuito sigue siendo la misma, es decir, IR = IL = I. Deja VR y Vl ser el Caída de tensión a través de la resistencia y el inductor.

Aplicando La ley de voltaje de Kirchhoff (es decir, la suma de la caída de voltaje debe ser igual a la aplicación de voltaje) a este circuito que obtenemos,

Diagrama de fósforo para el circuito RL

Antes de dibujar el diagrama de fases del circuito RL en serie…uno debe saber la relación entre el voltaje y la corriente en el caso de la resistencia y el inductor.

1. 1. Resistencia
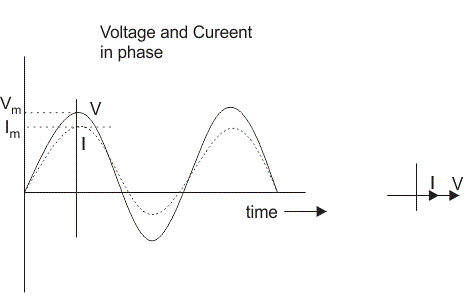
      En el caso de la resistencia, el voltaje y la corriente están en la misma fase o podemos decir que la diferencia de ángulo de fase entre el voltaje y la corriente es cero.

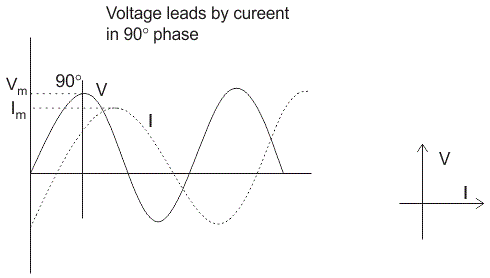
1. 1. Inductor
      En el inductor, el voltaje y la corriente no están en fase. El voltaje lleva al de la corriente en un 90o o en otras palabras, el voltaje alcanza su valor máximo y cero 90o antes de que la corriente lo alcance.

1. Circuito RL
   Para dibujar el diagrama de fases del circuito RL en serie, siga los siguientes pasos:

Paso… yo. En el caso de un circuito RL en serie, la resistencia y el inductor están conectados en serie, de modo que la corriente que fluye en ambos elementos es la misma, es decir, IR = IL = I. Por lo tanto, tome el fásor actual como referencia y dibújelo en el eje horizontal como se muestra en el diagrama.
Paso II. En el caso de la resistencia, tanto el voltaje como la corriente están en la misma fase. Así que dibuja el fásor del voltaje, VR a lo largo del mismo eje o dirección que el del fásor actual, es decir, VR está en fase con I.

Paso… III. Sabemos que en el inductor, el voltaje conduce la corriente en un 90oasí que dibuja VL (caída de voltaje a través del inductor) perpendicular al fásor de la corriente.
Paso… IV. Ahora tenemos dos voltajes VR y VL. Dibuja el vector resultante(VG) de estos dos voltajes. Como por ejemplo,
y del triángulo de ángulo recto obtenemos, el ángulo de fase


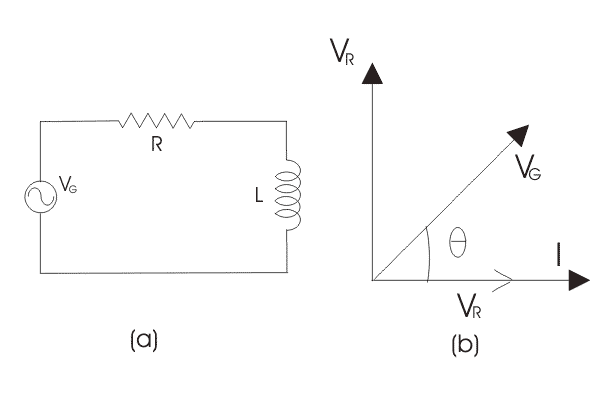
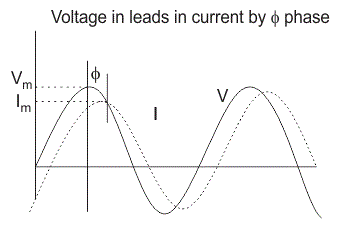
CONCLUSIÓN: En el caso de un circuito resistivo puro, el ángulo de fase entre el voltaje y la corriente es cero y en el caso de un circuito inductivo puro, el ángulo de fase es 90o pero cuando combinamos tanto la resistencia como el inductor, el ángulo de fase de un circuito RL en serie está entre 0o a 90o.

Impedancia del circuito RL en serie

La impedancia del circuito RL en serie se opone al flujo de corriente alterna. La impedancia del circuito RL en serie no es más que el efecto combinado de la resistencia (R) y la reactancia inductiva (XL) del circuito en su conjunto. La impedancia Z en ohmios está dada por,
Z = (R2 + XL2)0.5 y desde el triángulo de ángulo recto, el ángulo de fase = tan– 1(XL/R).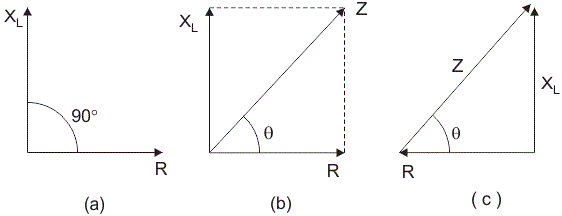

Análisis del circuito de la serie RL

En el circuito RL en serie, los valores de frecuencia f, voltaje V, resistencia R y inductancia L son conocidos y no existe un instrumento para medir directamente el valor de la reactancia e impedancia inductiva; por lo tanto, para un análisis completo del circuito de la serie RL, siga estos sencillos pasos:

Paso 1.Puesto que el valor de la frecuencia y el inductor son conocidos, en primer lugar calcular el valor de la reactancia inductiva XL: XL = 2fL ohms.
Paso 2. Del valor de XL y R, calculan la impedancia total del circuito que viene dada por

Paso 3. Calcular el ángulo de fase total para el circuito = tan – 1(XL/ R).
Paso 4. Utilice Ley de Ohms y encontrar el valor de la corriente total: I = V/Z amperio.
Paso 5. Calcule los voltajes a través de la resistencia R y el inductor L usando la Ley de Ohms. Como la resistencia y el inductor están conectados en serie, la corriente en ellos sigue siendo la misma.

Potencia en el circuito RL

En el circuito RL en serie, algo de energía es disipada por la resistencia y algo de energía es almacenada alternativamente y devuelta por el inductor-

1. La potencia instantánea entregada por fuente de tensión V es P = VI (vatios).
2. La energía disipada por la resistencia en forma de calor, P = I2R (vatios).
3. La velocidad a la que la energía se almacena en el inductor,

Así, la potencia total en el circuito RL en serie se da sumando la potencia disipada por la resistencia y la potencia absorbida por el inductor.

El triángulo de potencia para el circuito RL en serie se muestra a continuación,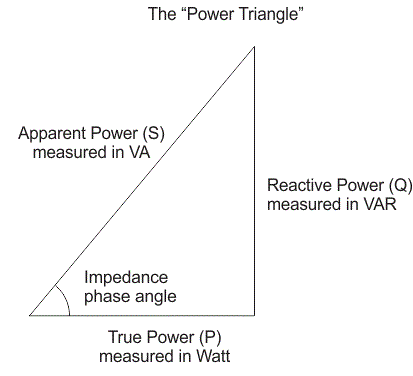

El el factor de potencia eléctrica cos se define como la relación entre la potencia real y la potencia aparente.

Variación de la impedancia y del ángulo de fase con la frecuencia

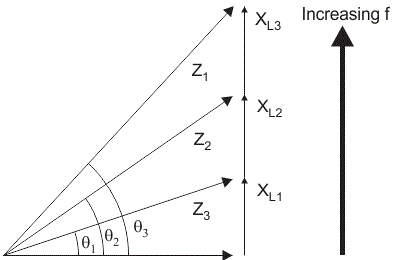
El diagrama anterior muestra el triángulo de impedancia. La base de este triángulo de impedancia representa resistencia. La resistencia es independiente de la frecuencia; así, si la frecuencia aumenta o disminuye, la resistencia permanece constante. La fórmula de la reactancia inductiva es XL = 2fL. Así que, si la frecuencia aumenta, la reactancia inductiva XL también aumenta y si la reactancia inductiva aumenta, la impedancia total del circuito también aumenta y esto lleva a la variación del ángulo de fase con la frecuencia. Así que, en el circuito RL en serie si la frecuencia aumenta,

1. La reactancia inductiva también aumenta, ya que es directamente proporcional a la frecuencia.
2. la impedancia total Z aumenta.
3. el ángulo de la fase aumenta.
4. resistencia permanece constante.

Expresión para la corriente que fluye en el circuito RL en serie

Considere un circuito en el que la resistencia está conectada en serie con el inductor y fuente de tensión de voltios V, se aplica a través de él. Inicialmente el interruptor está abierto. Digamos que en el momento t cerramos el interruptor y la corriente i empieza a fluir en el circuito pero no alcanza su máximo valor rápidamente debido a la presencia del inductor en el circuito ya que sabemos que el inductor tiene la propiedad de oponerse al cambio de la corriente que fluye a través de él.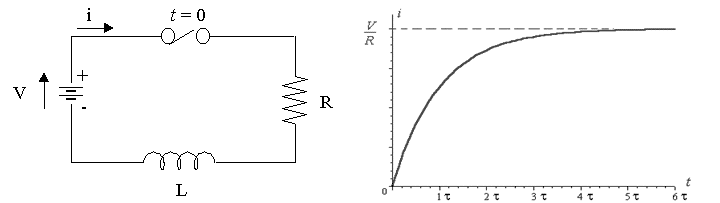

Aplicar la ley de voltaje Kirchhoffs en el circuito RL de la serie anterior,

Reordenando la ecuación anterior,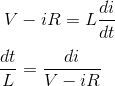

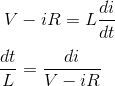
Integrando ambos lados, conseguimos,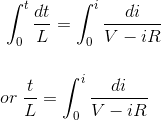

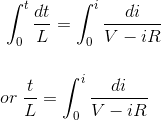
Ahora integre el lado derecho usando el método de sustitución,

Sustituyendo los valores que obtenemos,

Sabemos que la integración de,

Así que tenemos,

Aplicando límites conseguimos,

Simplificando de nuevo,

Tomando antilogía en ambos lados,

Sabemos que e En x = x, así que tenemos,

Moviendo el término que contiene la «i» por un lado tenemos,

El término L/R en la ecuación se llama la Constante de Tiempo, () de la Circuito de la serie RLy se define como el tiempo que tarda la corriente en alcanzar su máximo valor de estado estacionario y el término V/R representa el valor final de estado estacionario de la corriente en el circuito.