Análisis de la red es un proceso por el cual podemos calcular diferentes parámetros eléctricos de un elemento de circuito conectado en un red eléctrica. Un circuito eléctrico o red también puede ser complicada y en una red complicada, tenemos que aplicar diferentes métodos para simplificar la red para determinar los parámetros eléctricos. El elementos del circuito en una red puede conectarse de diferentes maneras, algunas de ellas en serie y otras en paralelo. El elementos del circuito son resistencias, condensadores, inductores, fuentes de tensión, fuentes de corriente etc. Actual, voltaje, resistencia…impedancia, reactancia, inductancia, capacitancia…la frecuencia, energía eléctrica, energía eléctrica etc. son los diferentes parámetros eléctricos que determinamos por análisis de la red. En resumen, podemos decir, un red eléctrica es la combinación de diferentes elementos de circuito y el análisis de red o análisis de circuito es la técnica para determinar los diferentes parámetros eléctricos de aquellos elementos del circuito.
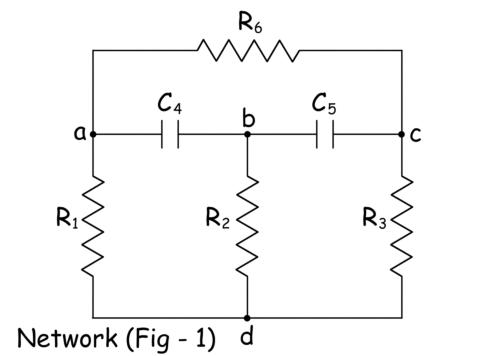
Gráfico de una red eléctrica
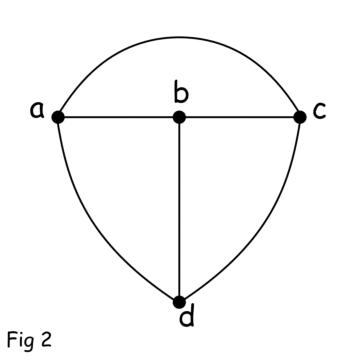
Cuando reemplazamos todos los elementos del circuito de una red eléctrica por líneas dibujadas a mano, entonces la figura se conoce como la gráfico de la red. La figura 2 de abajo muestra el gráfico de la red anterior en la figura 1.
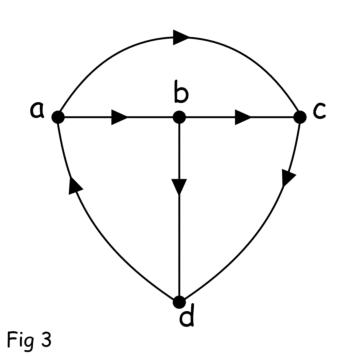
La línea representa que el elemento del circuito se llama la rama de una red. El punto donde dos o más ramas se encuentran se llama nodo de la red. La dirección de la corriente a través del elemento se representa con una punta de flecha dibujada en la rama. La dirección de la corriente en un gráfico puede ser considerada arbitrariamente. Cuando dibujamos un gráfico de una red con la dirección de la corriente (la dirección puede ser arbitraria) en cada una de las ramas, el gráfico se llama gráfico orientado de la red. La figura 3 muestra el gráfico orientado de la red anterior en la figura 1.
Cuando una red activa se representa como una red pasiva a través de un gráfico eliminando la fuentes de voltaje y corriente entonces el gráfico se conoce como el gráfico topológico orientado de la red. El fuente de tensión se elimina reemplazándolo por un cortocircuito y la fuente de corriente se elimina reemplazándolo por un circuito abierto.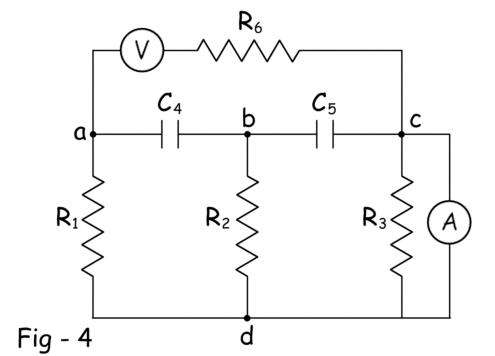
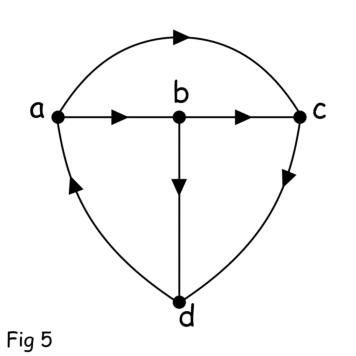
La anterior figura 4 mostraba una red eléctrica con ambos fuente de tensión y la fuente actual. La figura 5 muestra la gráfico topológico orientado de la red en la figura 4.
Definición de los términos utilizados en el análisis de redes
Rama
Cada línea dibujada a mano en un gráfico que representa el camino para el flujo de la corriente se llama rama.
Nodo
El punto final de la rama donde otras ramas se encuentran se llama nodo.
Subgraph
Este es un subconjunto de ramas de un gráfico.
Árbol
El árbol es un subgrafo que contiene todos los nodos del gráfico pero no forma ningún circuito cerrado. Si el gráfico tiene n número de nodos, el árbol tendrá (n 1) número de ramas. Las ramas de un árbol se denominan ramitas. Por lo tanto, un árbol también puede ser referido como un conjunto de ramas.
Cotree
El cotree es un subgrafo que contiene todas las ramas que no están incluidas en un árbol. El árbol es el complemento de un árbol.
Circuito equivalente
El principal paso del análisis de redes es simplificar la red comparativamente compleja a su forma simplificada. Normalmente se puede hacer combinando las impedancias en serie y en paralelo. A veces se requiere transformar algunas o todas las fuentes de tensión de la red en fuente de corriente y viceversa. Si consideramos cualquiera de los dos terminales de una red activa, obviamente habría un voltaje a través de los terminales y corriente a través de los terminales. Tras la simplificación de la red, a través de estos dos terminales, el voltaje y la corriente con respecto a los terminales permanecen inalterados con respecto al original. Aunque la estructura de la red ha cambiado significativamente. El circuito (o red) original y el circuito (o red) simplificado se denominan circuito equivalente el uno del otro. En el caso de una red pasiva, la impedancia a través de cualquiera de los dos terminales de referencia de la red sigue siendo la misma después de la simplificación de la red.
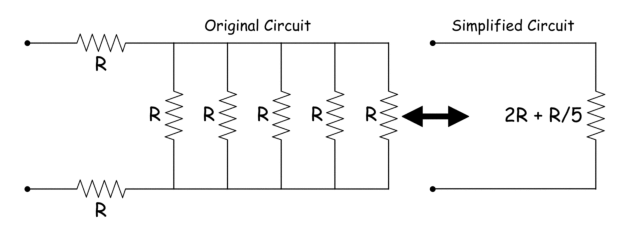
Circuito en serie y paralelo
Durante el análisis de la red, las actividades más frecuentes son la combinación de elementos de circuitos en serie y en paralelo.
Si n número de las resistencias están conectadas en serieel valor de la resistencia equivalente sería,
Si n número de las resistencias están conectadas en paraleloel valor de la resistencia equivalente sería,
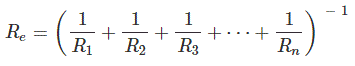
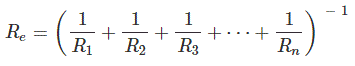
Si n número de las inductancias están conectadas en serieel valor de la inductancia equivalente sería,
Si n número de las inductancias están conectadas en paraleloel valor de la inductancia equivalente sería,
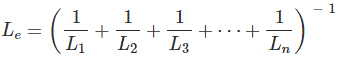
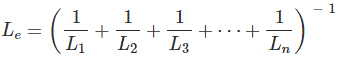
Si n número de las capacitancias están conectadas en serieel valor de la capacitancia equivalente sería,
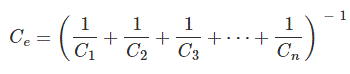
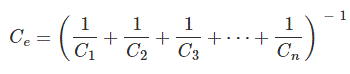
Si n número de las capacitancias están conectadas en paraleloel valor de la capacitancia equivalente sería,
Si se conectan en serie n número de impedancias, el valor de la impedancia equivalente sería,
Si n número de impedancias están conectadas en paralelo, el valor de la impedancia equivalente sería,
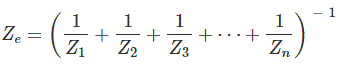
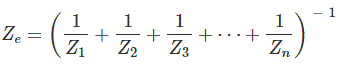
Transformación de la estrella Delta
En el caso de una red de dos terminales, las impedancias entre los puertos pueden simplificarse fácilmente mediante la combinación serie-paralela de las impedancias. Si el número de terminales de una red es superior a dos, es posible que la impedancia equivalente entre los terminales no se resuelva mediante una simple combinación en serie y en paralelo de las impedancias. Consideremos una red de tres terminales. Las impedancias o cualquier otro parámetro similar entre los puertos están conectadas en estrella o en triángulo. El red conectada delta puede convertirse en un red conectada en estrella y viceversa. Durante el análisis de la red, tenemos que transformar o bien delta en estrella o estrella en delta para simplificar la red. Consideremos una red de tres terminales formada por tres impedancias Za, Zby Zc conectado en la estrella. Considere otra red de tres terminales formada por tres impedancias Zab, Zbcy Zca. Si estas dos redes son equivalentes entre sí, entonces la relación entre las impedancias de la estrella y el delta sería la siguiente.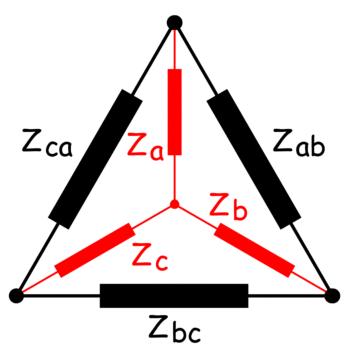 
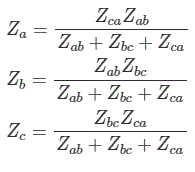
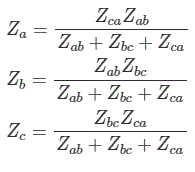
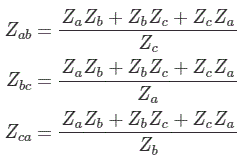
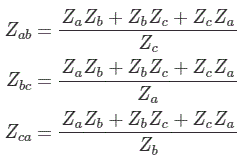
Transformación de la fuente eléctrica
Otro paso esencial muy utilizado durante el análisis de redes es transformación de la fuente. A menudo se hace esencial convertir las fuentes de corriente en fuentes de voltaje y las fuentes de voltaje en fuentes de corriente, para simplificar las complejas red eléctrica. En realidad un práctica fuente de voltaje puede considerarse como una fuente de voltaje ideal en serie con su resistencia interna. De la misma manera, una fuente de corriente práctica puede ser considerada como una fuente de corriente ideal en paralelo con su resistencia interna. Cuando una fuente de tensión se conecta a un circuito, impone su tensión a través de los terminales del circuito y entrega cierta corriente al circuito dependiendo de la impedancia del circuito y la resistencia interna en serie de la fuente. Se puede decir que una fuente de corriente es equivalente a la fuente de voltaje cuando la fuente de corriente entrega la misma corriente al circuito cuando se conecta a través de los mismos terminales. Se encuentra que la corriente de la fuente de corriente sería la corriente de cortocircuito de la fuente de voltaje y el valor de la resistencia interna es el mismo que el de la fuente de voltaje pero conectada en paralelo en lugar de en serie. Esto significa que si hacemos cortocircuito en dos terminales de una fuente de voltaje, la corriente que fluye a través del dispositivo es la corriente de la fuente de corriente equivalente. De forma similar, cuando una fuente de corriente está en circuito abierto, el voltaje que aparece a través del terminal abierto de la fuente sería el voltaje de la fuente de voltaje equivalente.
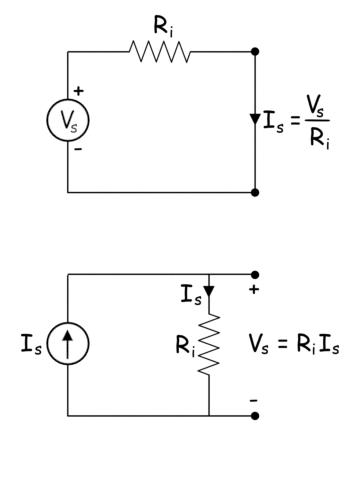
Regla de división de voltaje y corriente
Las técnicas más utilizadas para el análisis de redes son regla de división de voltaje y corriente. Regla de división de voltaje el proceso para calcular la caída de voltaje a través de una impedancia particular entre una serie de impedancias a través de una fuente de voltaje. Supongamos que hay n número de impedancias Z1, Z2, Z3 ..Zn conectados en serie a través de una fuente de voltaje Vs. Entonces la caída de voltaje a través de la impedancia Z1 es,
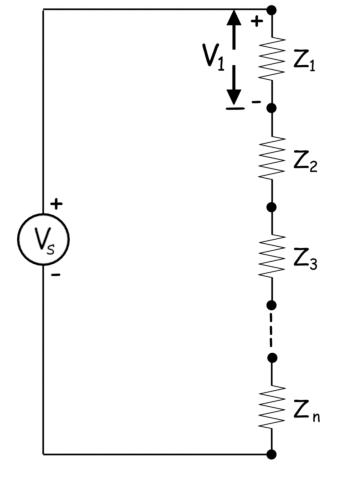
Aquí en la figura anterior hemos considerado las impedancias como resistencias pero podemos considerar cualquier otro parámetro de impedancia en lugar de la resistencia según el requisito del circuito.
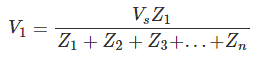
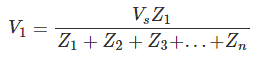
De manera similar, la caída de voltaje a través de cualquier impedancia particular Zi está dada por
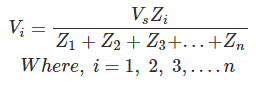
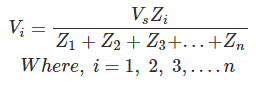
Tomemos una fuente de corriente Is conectado a través de n número de paralelo admisión Y1, Y2, Y3 Yn.
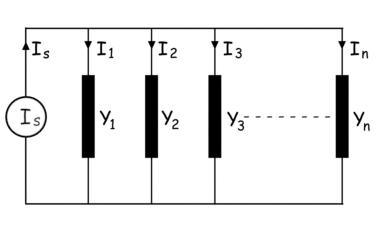
La corriente que pasa a través de la admisión Y1 se expresa como
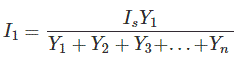
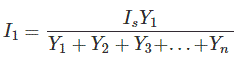
De manera similar, la corriente que pasa a través de la admisión Yi es,
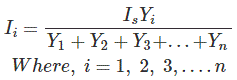
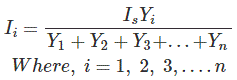
Análisis nodal y análisis de malla
Hay otros dos métodos importantes que se utilizan en el análisis de redes. Estos son el análisis nodal y el análisis de malla. No hace falta decir que estos dos métodos son los más comunes y los más utilizados en el análisis de redes. Estos dos métodos son análisis nodal y análisis de la malla. El análisis nodal de una red se ocupa principalmente de Ley actual de Kirchhoffs que dice que la corriente que entra en un nodo es igual a la corriente que sale del nodo. En otras palabras, la suma de todas las corrientes que entran y salen del nodo es igual a cero. Si un nodo (el punto de unión de las ramas de la red) tiene n número de ramas y I1, I2, I3 .. In son las corrientes a través de las respectivas ramas entonces,
La malla es el bucle de una red que no contiene ningún otro bucle en su interior. Los bordes de una red de malla están formados por las ramas de la red. Según análisis de la mallala suma del voltaje que aparece en cada rama sería cero. Eso significa que a lo largo de los bordes de una malla en cualquier dirección particular, el total de las ganancias de voltaje es exactamente igual al total de las caídas de voltaje. Esto no es más que Ley de tensión de Kirchhoffs. Si n número de ramas forman una malla y los voltajes a través de las respectivas ramas son V1, V2, V3y Vn…entonces podremos escribir,
Teorema de la superposición
Otro método popular de resolución de circuitos durante el análisis de redes es teorema de superposición. El método es aplicable a la red activa con más de una fuente eléctrica. En la técnica de superposición, primero tenemos que eliminar todas las fuentes por su impedancia interna excepto una. Primero se calcula el efecto de esta fuente en particular sobre una rama de la red. Esto significa que se calcula el voltaje o la corriente o ambos de esa rama para esa fuente conectada en la red. Luego quitamos la fuente manteniendo su impedancia interna en el lugar y reconectamos la segunda fuente en el lugar de la red. Ahora tenemos que calcular los parámetros necesarios de la misma rama. De esta manera, tenemos que reconectar y eliminar todas las fuentes una por una y calcular los parámetros requeridos cada vez. Por último, al sumar los efectos con el signo de todas las fuentes individuales en la rama obtenemos el efecto acumulado en la rama cuando todas las fuentes están conectadas a la red.
Teorema de Norton
El concepto de Teorema de Norton es bastante simple. Considere cualquier rama en un red eléctrica. Si la red está activa, debe haber cierta corriente que fluye a través de la rama. El origen de la corriente es la propia red activa y la cantidad de corriente que fluye por el brazo se debe a la impedancia equivalente de la red y a la impedancia de la propia rama. Como el resto de la red suministra corriente a la rama, la red puede considerarse una fuente ideal de corriente si la rama está en cortocircuito y con la impedancia equivalente de la red conectada en paralelo a la fuente. El proceso de simplificación de una red a una fuente de corriente equivalente fue desarrollado por Edward Lawry Norton y se conoce como Teorema de Norton.
Teorema de Thevenin
El concepto de Teorema de Thevenin es similar a la de Teorema de Nortonpero aquí toda la red activa es considerada como una fuente de tensión a través de la rama. El voltaje de la fuente es el voltaje de circuito abierto de la red a través del ramal y la impedancia de la fuente conectada en serie es la impedancia equivalente de la red a través del ramal. El proceso de simplificar una red activa a una sola fuente de tensión fue desarrollado por Leon Charles Thevenin.
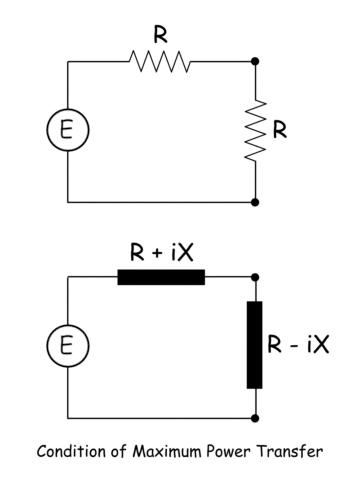
Teorema de transferencia de máxima potencia
En una red activa resistiva, cuando la resistencia equivalente de la red a través de un par de terminales es exactamente igual a la resistencia de la rama conectada a través de los terminales, se transferiría la máxima potencia a la rama resistiva de la red. Las redes que no son totalmente resistivas la Teorema de transferencia de máxima potencia puede definirse en la siguiente declaración. En una red activa, cuando la impedancia equivalente de la red a través de un par de terminales es un complejo conjugado de la impedancia de la rama conectada a través de los terminales, se transferiría la máxima potencia a la rama desde la red.
