Contenido
- ¿Qué es el Código Gris?
- Tabla de códigos grises
- Conversor de código binario a gris
- Cómo convertir el código binario en código gris
- Ejemplo de conversión de código binario a gris
- Conversor de código gris a binario
- Conversión de código gris a binario
- Ejemplo de conversión de código gris a binario
- Secuencia de ejemplo de código gris
- Aplicación del Código Gris
- Ventajas del Código Gris
- Desventajas del Código Gris
¿Qué es el Código Gris?
Código gris también conocido como Código Cíclico, Código binario reflejado (RBC), Binario reflejado (RB) o Código gris se define como un orden del sistema numérico binario de tal manera que cada valor incremental sólo puede diferir en un bit. En el código gris, mientras se viaja de un paso a otro paso sólo cambia un bit en el grupo de código. Es decir que dos números de código adyacentes difieren entre sí sólo por un bit.
El código gris es el más popular de los códigos de distancia de las unidades, pero no es adecuado para las operaciones aritméticas. El código gris tiene algunas aplicaciones en los convertidores analógicos a digitales, además de ser utilizado para la corrección de errores en la comunicación digital. El código gris puede ser difícil de entender inicialmente, pero se vuelve mucho más fácil de entender cuando se observan las tablas de códigos grises a continuación.
Tabla de códigos grises
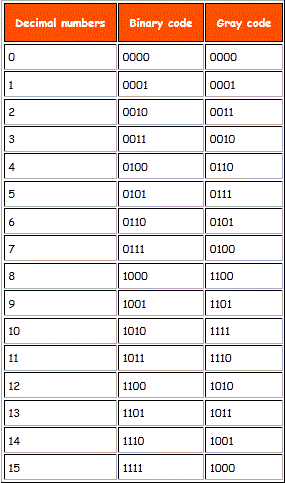
A continuación se muestra una tabla que muestra la conversión entre el código binario a código gris y el código decimal a código gris:

Conversor de código binario a gris
El circuito lógico que convierte el código binario en un código gris equivalente se conoce como convertidor de código binario a gris. Se puede obtener un código gris de n-bits reflejando un código de n-1 bits sobre un eje después del 2n-1 y poniendo el MSB (Most Significant Bit) de 0 por encima del eje y el MSB de 1 por debajo del eje. La reflexión de los códigos grises se muestra a continuación.
La tabla de conversión de códigos binarios a grises de 4 bits se presenta a continuación:


Esto significa que, en el código gris de 4 bits, (4-1) o el código de 3 bits se refleja contra el eje dibujado después de la (24-1)th o 8th fila.
El circuito convertidor de código binario a gris se muestra a continuación:
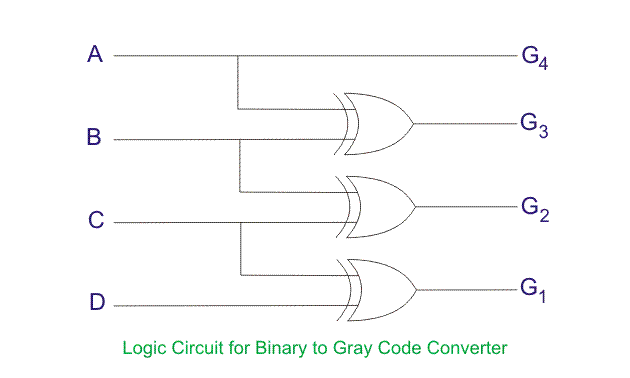

Cómo convertir el código binario en código gris
- El MSB (Most Significant Bit) del código gris será exactamente igual al primer bit del número binario dado.
- El segundo bit del código será exclusivo o (XOR) del primer y segundo bit del número binario dado, es decir, si ambos bits son iguales el resultado será 0 y si son diferentes el resultado será 1.
- El tercer bit del código gris será igual al exclusivo o (XOR) del segundo y tercer bit del número binario dado. Por lo tanto, la conversión de código binario a gris continúa. A continuación se da un ejemplo para ilustrar estos pasos.
Ejemplo de conversión de código binario a gris
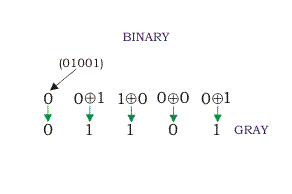
Digamos que tenemos un número binario 01001 que queremos convertir en código gris. Veamos un ejemplo de cómo realizaríamos esta conversión:
- El MSB se mantiene igual. Como el MSB del binario es 0, el MSB del código gris también será 0 (primer bit gris)
- A continuación, toma el XOR del primer y segundo bit binario. El primer bit es 0, y el segundo bit es 1. Los bits son diferentes, así que el bit gris resultante será 1 (segundo bit gris)
- A continuación, toma el XOR del segundo y tercer bit binario. El segundo bit es 1, y el tercero es 0. Estos bits son de nuevo diferentes, así que el bit gris resultante será 1 (tercer bit gris)
- A continuación, toma el XOR del tercer y cuarto bit binario. El tercer bit es 0, y el cuarto bit es 0. Como son iguales, el bit gris resultante será 0 (cuarto bit gris)
- Por último, toma el XOR del cuarto y quinto bit binario. El cuarto bit es 0, y el quinto bit es 1. Estos bits son diferentes, así que el bit gris resultante será 1 (quinto bit gris)
- Por lo tanto, el resultado de la conversión de código binario a código gris de 01001 está completo, y el código gris equivalente es 01101.

Conversor de código gris a binario
En un convertidor de código gris a binariola entrada es un código gris y la salida es su código binario equivalente.
Consideremos un convertidor de código gris a binario de 4 bits. Para diseñar un convertidor de código gris a binario de 4 bits, primero tenemos que dibujar una tabla de conversión de código gris, como se muestra a continuación:


El código gris del circuito convertidor binario se muestra a continuación:
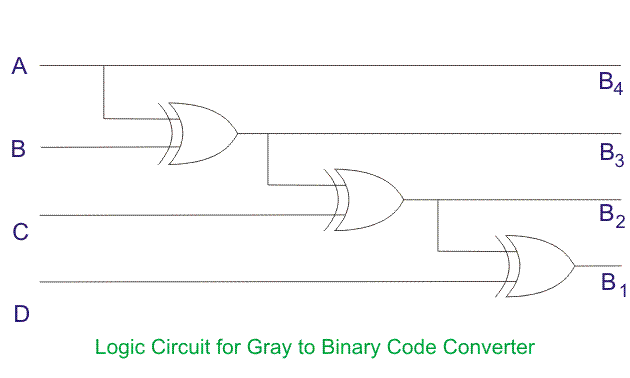

Conversión de código gris a binario
Conversión de código gris a binario es de nuevo un proceso muy simple y fácil. Los siguientes pasos pueden aclarar su idea sobre este tipo de conversiones.
- El MSB del número binario será igual al MSB del código gris dado.
- Ahora, si el segundo bit gris es 0, entonces el segundo bit binario será el mismo que el anterior o el primero. Si el bit gris es 1, el segundo bit binario se alterará. Si era 1 será 0 y si era 0 será 1.
- Este paso se continúa para que todos los bits hagan Conversión de código gris a binario.

Un ejemplo que se da a continuación aclarará su idea.
Ejemplo de conversión de código gris a binario
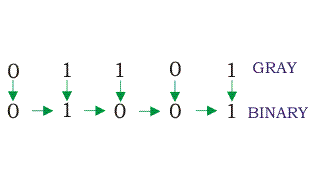
El MSB del binario será 0 como el MSB del gris es 0. Ahora pasa al siguiente bit de gris. Como es 1, el bit binario anterior se alterará, es decir, será 1, por lo que el segundo bit binario será 1. A continuación, miren el tercer bit del código gris. Como es de nuevo 1, por lo tanto el bit anterior, es decir, el segundo bit binario se alterará de nuevo y el tercer bit del número binario será 0. Ahora, el 4º bit del gris dado es 0, por lo que el bit binario anterior no cambiará, es decir, el 4º bit binario será 0. Ahora, de nuevo el 5º bit del gris es 1, por lo que el bit binario anterior se alterará, será 1 de 0. Por lo tanto, el número binario equivalente en el caso del código gris a la conversión binaria será (01001).



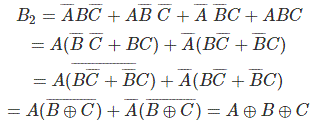
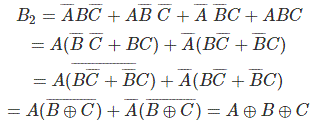

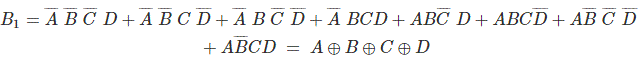
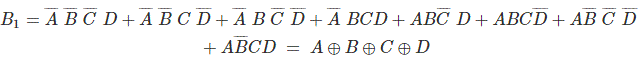
Secuencia de ejemplo de código gris
- El código gris sólo puede cambiar un bit de su paso anterior a su siguiente paso. El cambio de bit siempre se produce desde el lado derecho al izquierdo, es decir, desde el LSB (Least Significant Bit) hacia el MSB (Most Significant Bit).
- Sabemos que para el dígito binario hay dos posibles combinaciones 0 y 1. Siguiendo nuestra regla, primero apuntamos al LSB (lado derecho). De ahí que los tres primeros bits se mantengan constantes (es decir, 000) y el cuarto bit cambie de 0 a 1. Este es el equivalente decimal de 1.
- Ahora pasa al siguiente bit de la LSB, es decir, el 3er bit. Ahora cambiamos este bit de 0 a 1 que es el equivalente decimal para 2 (0011). Obsérvese que, a diferencia del binario, no podemos ir de 0001 a 0010, ya que esto es cambiar tanto el 3er bit (0 a 1) como el 4to bit (1 a 0) al mismo tiempo.
- Ahora para incrementar desde 0011, empezamos en el LSB (lado derecho) y observamos que no hemos visto la combinación 0010 hasta ahora. Como tal, mantenemos los tres primeros bits constantes y cambiamos el último bit de 1 a 0. Por lo tanto, el código gris para el número decimal 3 es 0010
- Travesía al siguiente código. No podemos cambiar el 3er o 4to bit como hemos visto estas combinaciones antes. Por lo tanto, pasamos al segundo bit y lo cambiamos de 0 a 1. Esto da el número decimal 4 como 0110 en código gris. Puedes preguntarte por qué no podemos cambiar el tercer bit de nuevo, que también será un cambio de un bit con respecto al anterior. Pero como cambiar el tercer bit daría el equivalente al código gris 0000 que ha ocurrido antes (número decimal 0), no podemos hacerlo. Recuerde que un número que ha ocurrido anteriormente no puede ser repetido.
- Repitiendo nuestros pasos anteriores, mantendremos constantes el primer y segundo bit y encontraremos las posibles combinaciones del tercer y cuarto bit cambiando sólo 1 bit en cada paso. Comenzaremos con el cuarto bit ya que este es el LSB.
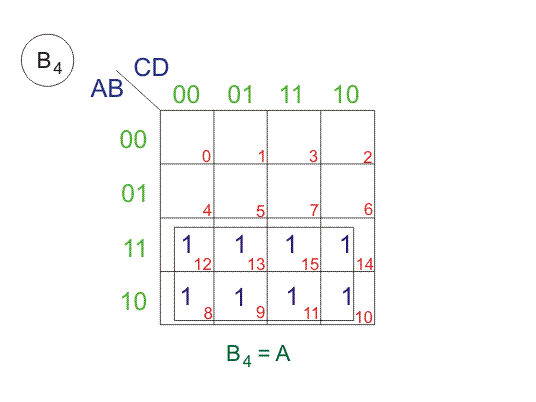
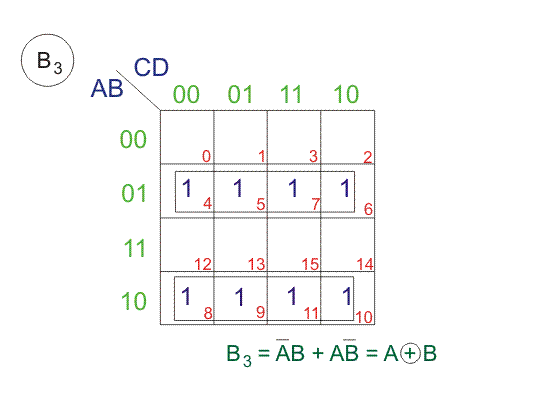
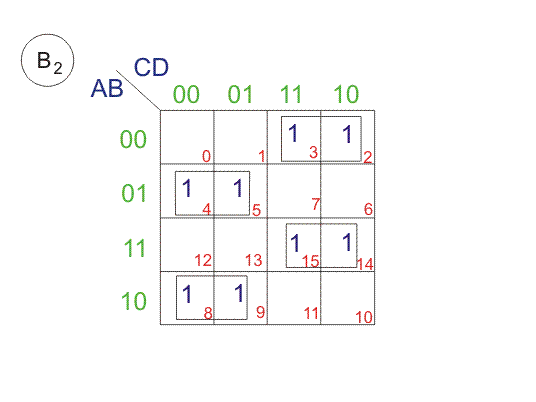
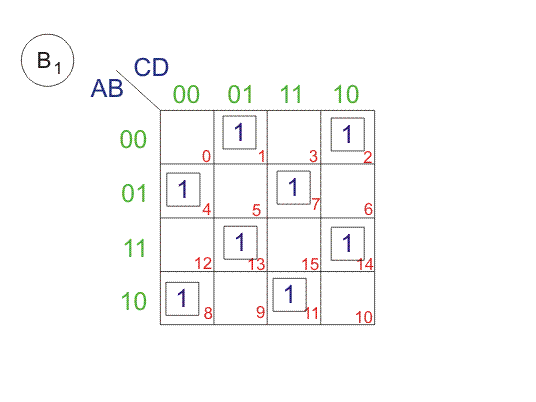
Los bits de código gris de 4 bits se consideran como G4G3G2G1. Ahora de la tabla de conversión,
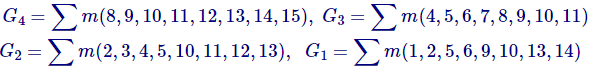
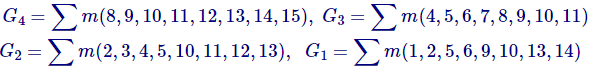
Desde arriba SOPs (Suma de Productos), dibujemos Los mapas de Karnaugh (K-maps) para G4, G3, G2, y G1.
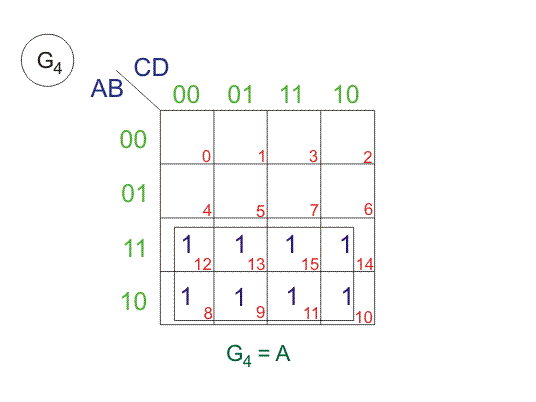

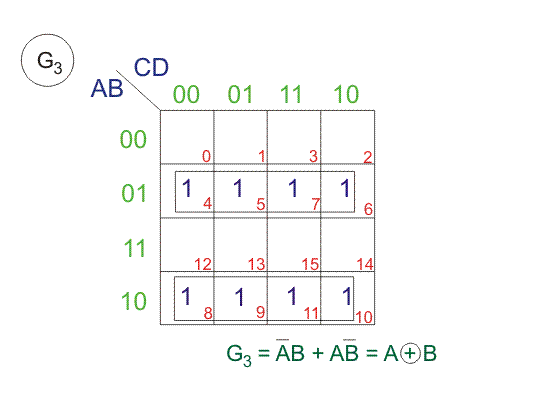

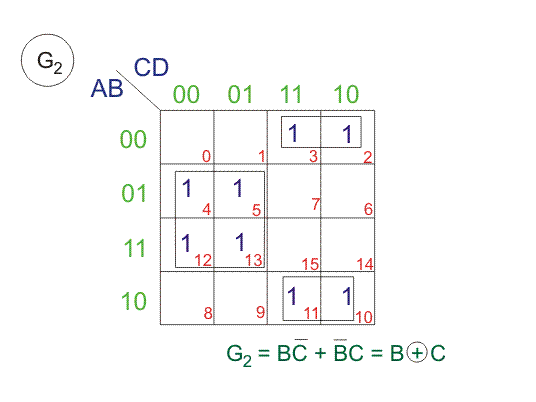

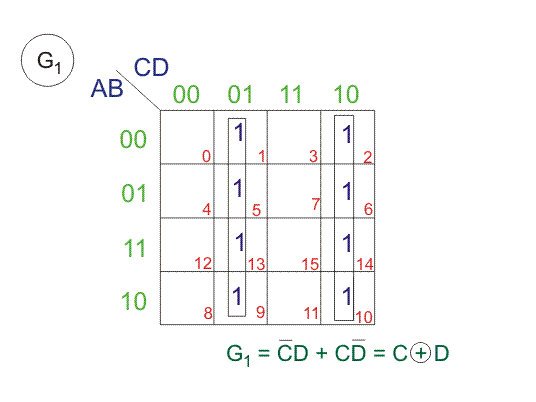

Aplicación del Código Gris
El código gris se utiliza en algunas aplicaciones específicas. Las principales aplicaciones incluyen ser usado en convertidores de analógico a digital, así como ser usado para la corrección de errores en la comunicación digital. El código gris se utiliza para minimizar los errores en la conversión de señales analógicas a digitales.
Frank Gray la persona código Gray fue nombrado después de patentar un tubo de Modulación de Código de Pulso (PCM). Este tubo PCM fue hecho por Raymond W. Sears de Bell Labs (trabajando con Frank Gray y William M. Goodall) que acreditó a Gray por la idea del código binario reflejado (es decir, el código gris). Puedes leer esto en televisión por modulación de código de pulso.
Algunas otras aplicaciones del código gris:
- Minimización del circuito booleano
- La comunicación entre los dominios del reloj
- Corrección de errores
- Algoritmos genéticos
- Puzzles matemáticos
- Codificadores de posición
Ventajas del Código Gris
- Mejor para la minimización de errores en la conversión de señales analógicas a señales digitales
- Reduce la aparición de Hamming Walls (un estado indeseable) cuando se utiliza en algoritmos genéticos
- Se puede usar para minimizar un circuito lógico
- Útil en cruce del dominio del reloj
Desventajas del Código Gris
- No es adecuado para operaciones aritméticas
- Uso práctico limitado fuera de unas pocas aplicaciones específicas