Álgebra booleana es un tipo diferente de álgebra o más bien puede decirse que un nuevo tipo de álgebra que fue inventada por el famoso matemático George Boole en el año 1854. Lo publicó en su libro «Una investigación de las leyes del pensamiento». Más tarde, usando esta técnica, Claude Shannon introdujo un nuevo tipo de álgebra que se denomina Cambiando el álgebra. En electrónica digital hay varios métodos para simplificar el diseño de los circuitos lógicos. Este álgebra es uno de estos métodos. De acuerdo con George Boole los símbolos pueden usarse para representar la estructura de los pensamientos lógicos. Este tipo de álgebra se ocupa de las reglas o leyes, que se conocen como leyes del álgebra de Boole por el cual se llevan a cabo las operaciones lógicas.
También hay pocos los teoremas del álgebra booleanaque deben ser notados cuidadosamente porque esto hace que el cálculo sea más rápido y fácil. La lógica booleana se ocupa sólo de dos variables, 1 y 0, por las cuales se deben realizar todas las operaciones matemáticas.
Álgebra booleana o álgebra de cambio es un sistema de lógica matemática para realizar diferentes operaciones matemáticas en sistema binario. Sólo hay tres operaciones binarias básicas, Y, O y NO por las que se deben hacer todas las operaciones matemáticas binarias simples y complejas. Hay muchas reglas en el álgebra booleana por las que se hacen esas operaciones matemáticas. En el álgebra booleana, las variables están representadas por la letra mayúscula inglesa como A, B, C, etc. y el valor de cada variable puede ser 1 o 0, nada más. En el álgebra booleana una expresión dada también puede ser convertida en un diagrama lógico usando diferentes puertas lógicas como Y la puerta, Puerta de la sala de operaciones y NO es una puerta, Puertas NOR, Puertas NAND, Puertas XOR, Puertas XNOR etc.
Algunas operaciones booleanas lógicas básicas,
Y Operación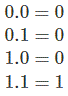
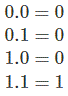
Operación de quirófano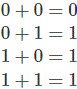
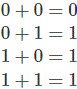
No Operación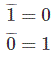
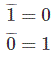
Algunas leyes básicas del Álgebra Booleana
A . 0 = 0 donde A puede ser 0 o 1.
A . 1 = A donde A puede ser 0 o 1.
A . A = A donde A puede ser 0 o 1.
A . = 0 donde A puede ser 0 o 1.
A + 0 = A, donde A puede ser 0 o 1.
A + 1 = 1 donde A puede ser 0 o 1.
A + = 1
A + A = A
A + B = B + A donde A y B pueden ser 0 o 1.
A . B = B . A donde A y B pueden ser 0 o 1.
Las leyes del álgebra booleana también son válidas para más de dos variables como,
Ley acumulativa del álgebra de Boole
Según el Derecho acumulativo, el orden de Operaciones de quirófano y Y operaciones …realizado en las variables no hace diferencias.
Leyes asociativas para el álgebra de Boole
Esta ley es para varias variables, donde la operación OR del resultado de las variables es la misma a través de la agrupación de las variables. Esta ley es muy similar en el caso de los operadores AND.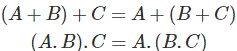
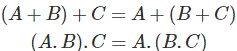
Leyes de distribución del álgebra de Boole
Esta ley está compuesta por dos operadores, AND y OR.
Mostremos un uso de esta ley para probar la expresión 
Prueba: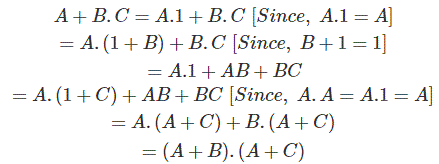
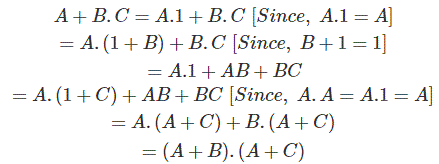
Regla literal redundante
De tabla de la verdad,
| Aportes | Salida | ||
| A | B | B | A + B |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 |
| Aportes | Salida | |
| A | B | A+B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
De la tabla de la verdad se demuestra que,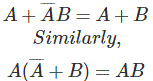
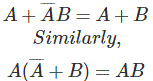
Leyes de absorción del álgebra de Boole
Prueba de la tabla de la verdad,
| Aportes | Salida | ||
| A | B | AB | A+A.B |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Tanto la columna A como la A+A.B son iguales.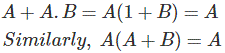
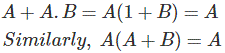
La prueba de tabla de la verdad,
| A | B | A+B | A.X(A+B) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
Tanto la columna A y A.X o A(A+B) son iguales.
De Morgans Therem,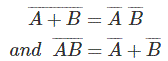
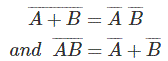
Prueba de la tabla de la verdad,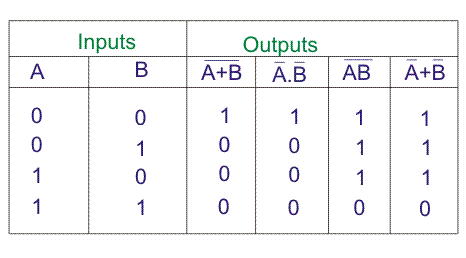
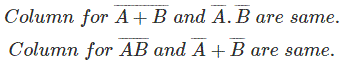
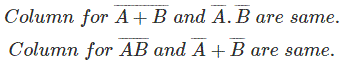
Ejemplos de Álgebra Booleana
Este es otro método para simplificar la compleja expresión booleana. En este método sólo usamos tres simples pasos.
- Complementa toda la expresión booleana.
- Cambie todos los OR por AND y todos los AND por OR.
- Ahora, complementen cada una de las variables y obtengan la expresión final.
Por este método,
se complementará primero, es decir.
Ahora, cambia todo (+) por (.) y (.) por (+), es decir.
Ahora, complementa cada una de las variables,
Esta es la forma final simplificada de la expresión booleana,
Y es exactamente igual a los resultados que se han obtenido aplicando Teorema de De Morgan.
Otro ejemplo,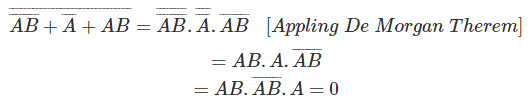
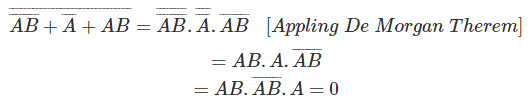
Por el segundo método,
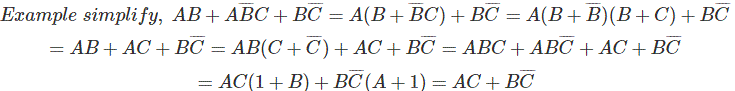
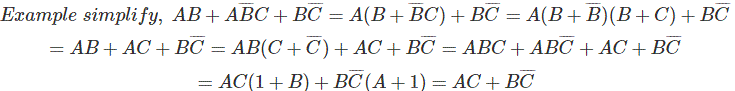
Representación de la función booleana en tabla de la verdad.
Consideremos una función booleana,
Ahora representemos la función en la tabla de verdad.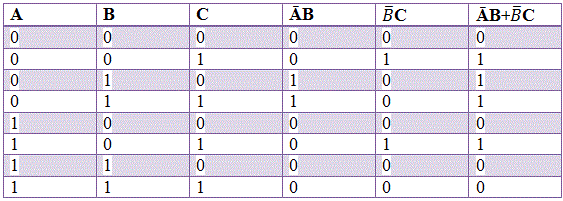
Por lo tanto, hemos mostrado algunas leyes del álgebra de Boole. En la otra página hemos descrito los teoremas de De Morgan y las leyes relacionadas con ellos.
