Hemos conocido el funcionamiento básico de aritmética binaria como adición binaria, sustracción binaria, multiplicación binaria y división binaria. Ahora vamos a ver la parte más importante de aritmética binaria en el que un montón de Álgebra booleana está de pie, es decir Teorema de De-Morgans que se llama Leyes de De-Morgans a menudo.
Antes de discutir Los teoremas de De-Morgans deberíamos saber sobre los cumplidos. Los complementos son el valor inverso al valor existente. Estamos tratando de decir que como solo hay dos dígitos en sistema numérico binario 0 y 1. Ahora si A = 0 entonces el complemento de A será 1 o A = 1.
En realidad hay dos teoremas que fueron propuestos por De-Morgan. Sobre la base de Las leyes de DE Morgans mucho Álgebra booleana están resueltos. La resolución de estos tipos de álgebra con el teorema de De-Morgans tiene una gran aplicación en el campo de electrónica digital. El teorema de De Morgan se puede enunciar de la siguiente manera:-
Teorema 1:
El complemento del producto de dos variables es igual a la suma del complemento de cada variable.
Así, según Leyes de De-Morgans o el teorema de De-Morgans si A y B son las dos variables o números booleanos. Entonces, en consecuencia
Teorema 2:
El complemento de la suma de dos variables es igual al producto del complemento de cada variable.
Así, según el teorema de De Morgans, si A y B son las dos variables entonces.
Leyes de De-Morgans también se puede implementar en el álgebra booleana en los siguientes pasos:-
- Mientras hacía Álgebra booleana al principio reemplazar al operador dado. Es decir, si (+) está ahí, entonces reemplácelo con (.) y si (.) está ahí, entonces reemplácelo con (+).
- El siguiente cumplido de cada uno de los términos se encuentra.
El teorema de De-Morgans puede probarse mediante el simple método de inducción del cuadro que figura a continuación.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A | B | A | B | A+B | A.B | (A+B) | A.B | (A.B) | A+B |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
Ahora mira la tabla con mucho cuidado en cada fila. Primero el valor de A = 0 y el valor de B = 0. Ahora para estos valores A = 1, B = 1. De nuevo A + B = 0 y A.B = 0. Así (A + B) = 1 y (A.B) = 1, A + B = 1 y A.B = 1. Por lo tanto, de esta tabla se puede ver que el valor de las columnas nº 7 y 8 son iguales y que las columnas nº 9 y 10 también son iguales, lo que prueba el teorema de De-Morgans.
De nuevo diferentes valores de A y B vemos la misma cosa, es decir, la columna nº 7 y 8 son iguales entre sí y la 9 y 10 son iguales entre sí. Así que por esto tabla de la verdad podemos probar el teorema de De-Morgans.
Algunos ejemplos que se dan a continuación pueden aclarar su idea.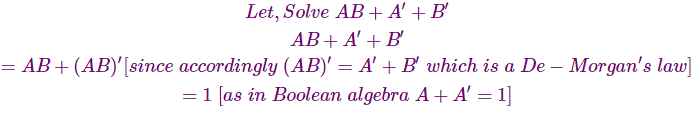
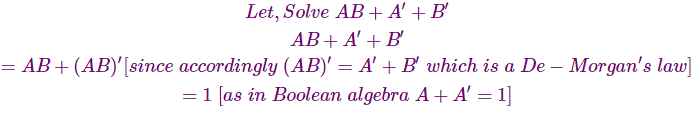
Por lo tanto,
Con la ayuda del teorema de De-Morgans nuestros cálculos se hacen mucho más fáciles.
Que sea otro ejemplo,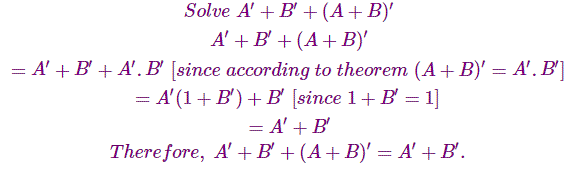
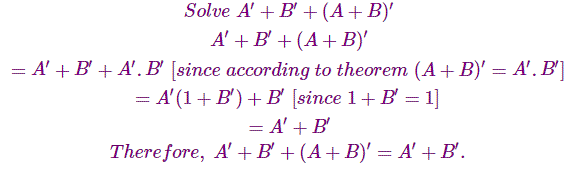
En ambas ecuaciones hemos usado adecuadamente Leyes de De-Morgans para hacer nuestro cálculo mucho más fácil.


