Antes de saber sobre Complemento de los 9s y 10s complemento deberíamos saber por qué se usan y por qué su concepto llegó a existir. Los complementos se utilizan para facilitar las operaciones aritméticas en el sistema digital. En este artículo hablaremos de los siguientes temas
- Complemento de los 9s
- 10s complemento
- 9s complemento de la sustracción
- 10s complementos de sustracción
Ahora, primero que nada, déjenos saber qué es el complemento 9s y cómo se hace. Para obtener el complemento de 9s de cualquier número tenemos que restar el número con (10n 1) donde n = número de dígitos del número, o de una manera más simple tenemos que dividir cada dígito del número decimal dado con 9. La tabla que se muestra a continuación explicará el complemento de 9s más fácilmente.
| Dígito decimal | Complemento de los 9s |
| 0 | 9 |
| 1 | 8 |
| 2 | 7 |
| 3 | 6 |
| 4 | 5 |
| 5 | 4 |
| 6 | 3 |
| 7 | 2 |
| 8 | 1 |
| 9 | 0 |
Ahora vamos a 10s complementoes relativamente fácil encontrar el complemento de 10 después de encontrar el complemento de 9 de ese número. Tenemos que sumar 1 con el Complemento de los 9s de cualquier número para obtener el deseado complemento de 10 de ese número. O si queremos averiguar el complemento de 10 directamente, podemos hacerlo siguiendo la siguiente fórmula, (10n número), donde n = número de dígitos del número. A continuación se da un ejemplo para ilustrar el concepto de obtención del complemento 10s.
Tomemos un número decimal 456, el complemento de 9s de este número será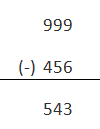
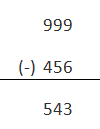
10s complemento de este no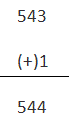
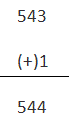
9s complemento de la sustracción
Entenderemos este método de sustracción a través de un ejemplo
A = 215
B = 155
Queremos averiguar el método de sustracción del complemento A-B por 9s
Primero tenemos que averiguar el complemento 9s de B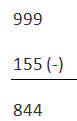
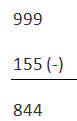
Ahora tenemos que añadir Complemento de los 9s de B a A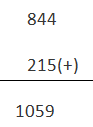
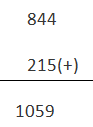
La parte izquierda del resultado se llama «carry» y se añade a la parte del resultado sin ella.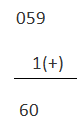
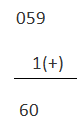
Se da otro tipo de ejemplo diferente
A = 4567
B = 1234
Tenemos que averiguar que A B
9s complemento de B
8765
Añadiendo 9s complemento de B con A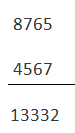
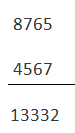
Añadiendo la carga con el resultado que obtenemos
3333
Ahora la respuesta es 3333
NB: Si no hay carry la respuesta será (9s complemento de la respuesta)
Sustracción por 10s complementos
De nuevo mostraremos el procedimiento con un ejemplo
Tomando los mismos datos
A = 215
B = 155
10s complemento de B = 845
Añadiendo el complemento 10s de B a A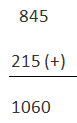
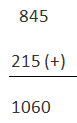
En este caso se omite el porte
La respuesta es 60
Tomando el otro ejemplo
A = 4567
B = 1234
10s complemento de B = 8766
Añadiendo 10 complementos de B con A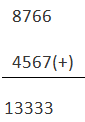
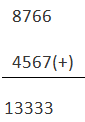
Para obtener la respuesta se ignora la carga
Entonces, la respuesta es 3333
NB: Si hay un carry entonces la respuesta es (10s complemento de la suma obtenida)