Álgebra booleana o álgebra de cambio es un sistema de lógica matemática para realizar diferentes operaciones matemáticas en el sistema binario. Estos son sólo dos elementos 1 y 0 por los cuales todas las operaciones matemáticas deben ser realizadas. Sólo hay tres operaciones binarias básicas, Y, O y NO, por las cuales se deben realizar todas las operaciones matemáticas binarias simples y complejas. Hay muchas reglas en el álgebra booleana por las que se realizan esas operaciones matemáticas.
En Álgebra booleanalas variables están representadas por letras mayúsculas inglesas como A, B, C, etc. y el valor de cada variable puede ser 1 o 0, nada más.
Algunas operaciones booleanas lógicas básicas…
Y operación,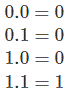
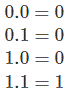
Operación de quirófano,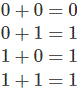
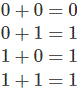
No es una operación,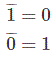
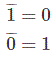
Algunas leyes básicas para Álgebra Booleana,
A . 0 = 0 donde A puede ser 0 o 1.
A . 1 = A donde A puede ser 0 o 1.
A . A = A donde A puede ser 0 o 1.
A . = 0 donde A puede ser 0 o 1.
A + 0 = A, donde A puede ser 0 o 1.
A + 1 = 1 donde A puede ser 0 o 1.
A + = 1
A + A = A
A + B = B + A donde A y B pueden ser 0 o 1.
A . B = B . A donde A y B pueden ser 0 o 1.
Las leyes de Álgebra booleana también son verdaderos para más de dos variables como,
Leyes acumulativas para el álgebra booleana
![]()
![]()
Leyes asociativas para el álgebra de Boole
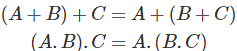
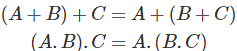
Leyes de distribución del álgebra de Boole
Regla literal redundante
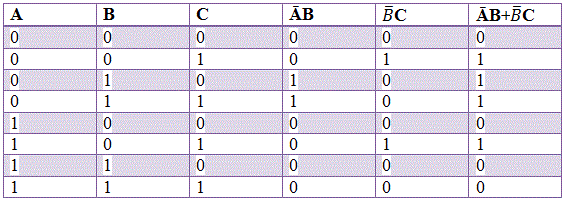
De tabla de la verdad,
| Aportes | Salida | ||
| A | B | B | A + B |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 |
| Aportes | Salida | |
| A | B | A+B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
De la tabla de la verdad se demuestra que,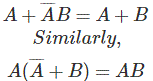
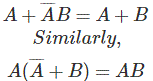
Leyes de absorción del álgebra de Boole
Prueba de la tabla de la verdad,
| Aportes | Salida | ||
| A | B | AB | A+A.B |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Tanto la columna A como la A+A.B son iguales.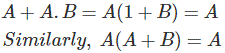
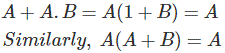
La prueba de tabla de la verdad,
| A | B | A+B | A.X(A+B) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
Tanto la columna A y A.X o A(A+B) son iguales.
De Morgans Therem,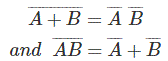
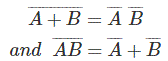
La prueba de tabla de la verdad,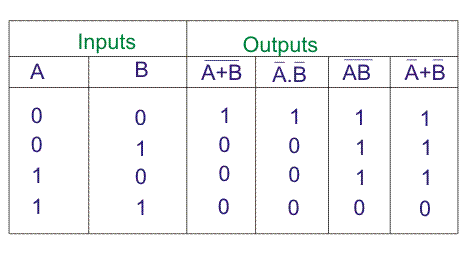

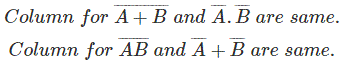
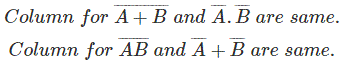
Ejemplos de Álgebra Booleana
![]()
![]()


Este es otro método para simplificar la compleja expresión booleana. En este método sólo usamos tres simples pasos.
- Complementa toda la expresión booleana.
- Cambie todos los OR por AND y todos los AND por OR.
- Ahora, complementen cada una de las variables y obtengan la expresión final.
Por este método,![]()
![]() se complementará primero, es decir.
se complementará primero, es decir.


![]()
![]()
Y es exactamente igual a los resultados que se han obtenido aplicando Teorema de De Morgan.
Otro ejemplo,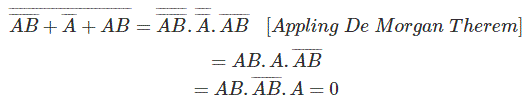
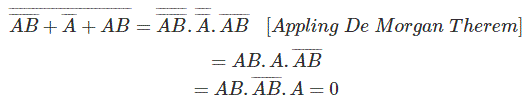
Por el segundo método,

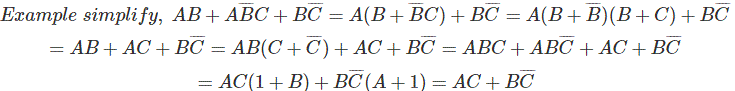
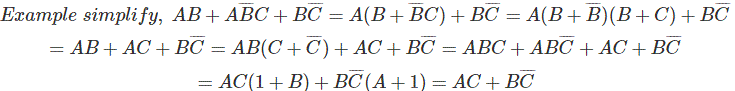
Representación de la función booleana en la tabla de la verdad.
Consideremos una función booleana,

Ahora representemos la función en tabla de la verdad.