2s complemento tiene una interesante propiedad que el aritmética binaria La operación puede realizarse fácilmente con números firmados o sin firmar. Da como resultado un complemento de 2s correcto.
¿Cómo representar el número decimal en el complemento de 2s?
Tomemos un número. El negativo firmado ese número es tal suma de números que con este número es cero. Tomemos ejemplos de nuestro sistema numérico más familiar que es el sistema decimal.
Dónde,
En el sistema binario sólo hay dos dígitos 0 y 1. En sistema binario todos y cada uno de los números y su signo se representan utilizando sólo estos dos dígitos 0 y 1. Como los signos negativos y positivos no pueden escribirse directamente en el sistema binario, tenemos que encontrar algún método alternativo para representarlos.
Para ello aprovechamos la definición de número negativo. Si tenemos que representar un número binario negativo, tenemos que encontrar una suma de números binarios cuyo número binario original sin signo o positivo sea cero. Como la suma de estos dos números es cero, el segundo número se toma como equivalente negativo del primer número.
Supongamos que tenemos que escribir 5 en binario que es negativo de 5 o + 5. Ahora 5 o + 5 puede ser representado en byte binario o sistema de 8 bits como 0000 0101 y el cero se representa en byte binario o sistema de 8 bits como 0000 0000.

Por lo tanto, este resultado es la representación de (- 5)10.
Ahora vamos a examinar 2s complemento de 0000 0101 y esto es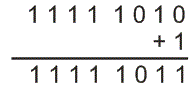
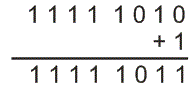
Por lo tanto, se demuestra que el cero menos cualquier número binario no es más que un complemento de 2s de este número, por lo tanto el complemento de 2s de cualquier número binario puede representarse como el equivalente negativo de ese número. En el complemento 2s primero convertimos un número decimal en un sistema numérico binario. Supongamos que queremos representar (5)10 en el complemento binario 2s. Representación binaria de (5)10 es (0000 0101)2.
Ahora el hecho interesante es que la forma sin firmar (5)10 en el complemento de 2s es la representación directa de la forma binaria de (5)10 es decir (0000 0101)2. El número no firmado se trata como un número positivo. El número decimal firmado puede ser un número positivo o negativo. Ahora para calcular 2s complemento para un número decimal firmado, es decir, (-5)10tenemos que averiguar el 1s complemento y luego convertir cada dígito en su dígito opuesto (es decir, 1 en 0 o 0 en 1) y añadir 1 al final. Este resultado después de la suma es la representación completa de 2s del número decimal con signo (negativo).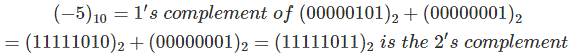
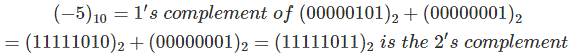
Ahora mira la tabla de abajo.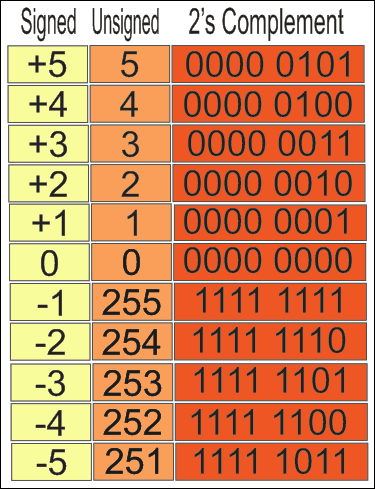

(+5)10 es igual que (5)10. Pero para (-1)10 se trata como no firmado (255)10. (-5)10 ⇔ (251)10
Tenga siempre presente que los números de complemento de 2s negativos siempre se representan como el número binario de tal manera que cuando se suman a un número positivo de la misma magnitud deben ser cero.
Lo importante es tener en cuenta que el bit más izquierdo o significativo indica el signo del entero. También se llama el bit con signo.
- Si el bit más a la izquierda es cero, entonces el número es positivo.
- Si el bit más izquierdo es uno, entonces el número es negativo.
Aritmética en 2s Método de Complemento
2s Complemento de la adición
La adición en el complemento de 2s, siempre sigue la misma regla que se utiliza en el normalmente adición binaria. Supongamos que queremos añadir (8)10 y (-3)10.
Primero tenemos que convertirlos en 2s complemento y simplemente añadirlos.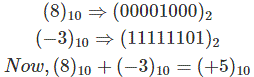
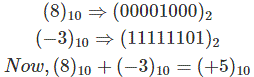
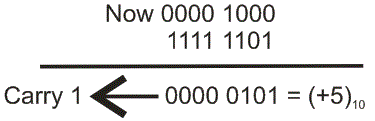

Como la carga es 1, entonces el número es positivo. Aquí el acarreo es 1 y es de 8 bits, por lo que no se considera en byte y por lo tanto la respuesta es un número positivo de un byte de largo. Así que está claro que para los números con y sin signo la adición puede realizarse fácilmente en el complemento de 2s.
2s Sustracción del complemento
La resta en el complemento de 2s sigue la misma regla que en la adición normalmente binaria. Lo único es que aquí la resta se convierte primero en su forma negativa y luego se añade con el minuendo. Supongamos que queremos restar (8)10 de (9)10. Primer converso (8)10 de (-9)10 en un complemento de 2s y simplemente añadir.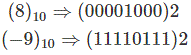
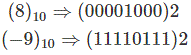
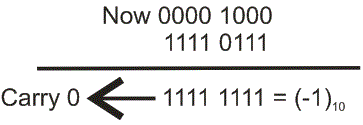

Como la carga es 0, entonces el número es negativo. Así que está claro que la sustracción se puede realizar fácilmente en 2s complemento fácilmente.
Multiplicación del complemento 2s
Para la multiplicación del complemento de 2s, siempre sigue las mismas reglas que multiplicación binaria. Supongamos que queremos multiplicar (- 4)10 con (4)10 que da (-16)10. Ahora, (- 4)10 = 1111 1100 en 2s complemento y (4)10 = 0000 0100 en 2s complemento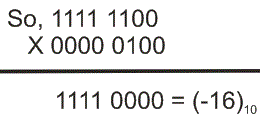
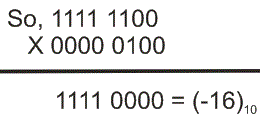
2s División de Complementos
Para la división del complemento 2s, el método es la sustracción del complemento 2s repetidamente. Primero se calcula el complemento de 2s del divisor y luego este divisor convertido debe ser añadido al dividendo. Ahora pasemos al siguiente ciclo de sustracción. Aquí el cociente reemplaza al dividendo. Repítelo una y otra vez hasta que el cociente se vuelva demasiado pequeño o cero. Si no es cero, entonces se trata como el resto. Supongamos que queremos calcular (7)10 ÷ (3)10la respuesta da (2)10 como cociente y (1)10 como el resto. Ahora vamos a empezar a calcularlo en 2s complemento.

Como la repetición es en dos rondas, entonces el cociente es (2)10.

