A fin de derivar varias condiciones de poder en ambos alternadores y motores síncronosConsideremos el problema general del flujo de energía a través de la impedancia inductiva. El diagrama de circuito que se muestra a continuación consiste en fuente de tensión E1, fuente de voltaje E1 y la carga que consiste en una resistencia en serie con un inductor. Ahora bien, si asumimos que la fuente de voltaje E1 es mayor que la fuente de voltaje E2 entonces el voltaje La ecuación de este circuito está dada por la ecuación,
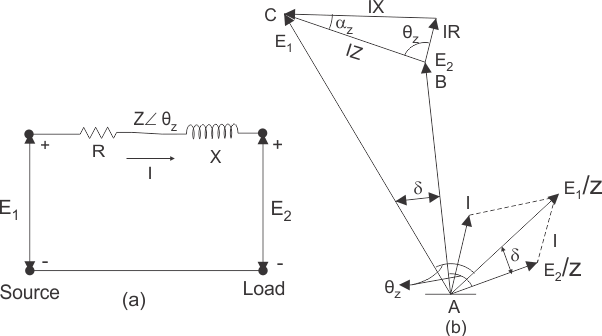



Donde, Z es R + jX como se muestra en el diagrama de circuito anterior.
De la expresión anterior escribimos la expresión de actual como![]()
![]()
Diagrama de fósforo para el circuito de arriba
Aquí discutiremos la forma más simple de dibujar el diagrama de fases para el circuito anterior. Antes de dibujar el diagrama fásico, escribamos las distintas anotaciones para cada cantidad en un lugar. Aquí lo utilizaremos:
θz para representar el ángulo entre el voltaje E1 y la actual E1/Z o el voltaje E2 y la actual E2/Z
I para representar la corriente en el circuito anterior y para representar el ángulo entre E1 y E2.
A continuación se muestra el diagrama de fases del circuito anterior: Para dibujar el diagrama de los fáseres, primero dibuje el E1 y la corriente E1/Z, marca el ángulo E1 y E1/Z comoz. De manera similar, dibujar el fásor E2 y E2/Z, de tal manera que el ángulo entre E1 y E2 debería ser… Completa el diagrama de los fáseres dibujando el caídas de tensión IX e IR como se muestra arriba. Ahora vamos a derivar la expresión para la energía suministrada por la fuente E1.
Deje que la energía suministrada por la fuente E1 ser P1. Definimos el poder como el producto de la voltaje y corriente, usando esto podemos escribir desde el diagrama de fases como P1=E1*(componente de la corriente I en fase con la fuente de tensión E1). Componente de la corriente en fase con la fuente de voltaje E1 es![]()
![]()
Al sustituir esta expresión en la ecuación anterior tenemos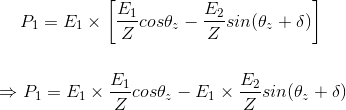
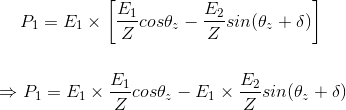
Desde el diagrama de fáseres, tenemosz = 90o z. Al sustituir el valor del ánguloz en la expresión anterior tenemos![]()
![]()
Esta es la expresión requerida para la energía suministrada por la fuente E1.
Deje que la energía suministrada por la fuente E2 ser P2. Definimos el poder como el producto de la voltaje y corriente, usando esto podemos escribir desde el diagrama de fases como

Componente de la corriente en fase con el fuente de tensión E2 es![]()
![]()
Al sustituir esta expresión en la ecuación anterior tenemos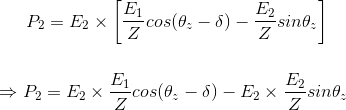
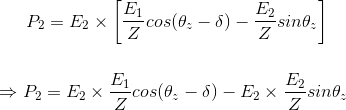
Desde el diagrama de fáseres, tenemosz = 90o z. Al sustituir el valor del ánguloz en la expresión anterior tenemos![]()
![]()
Esta es la expresión requerida para la energía suministrada por la fuente E2.
Ahora vamos a derivar varias ecuaciones para el flujo de energía del alternador de rotor cilíndrico. Para deducir la ecuación de potencia de un alternador, sustituimos la fuente de tensión E1 igual al voltaje de excitación (Ef), fuente de voltaje E2 es igual al voltaje terminal (Vt), la impedancia inductiva del circuito anterior es igual a la impedancia sincrónica (Zs) y Zs = ra + jXs. Después de reemplazar todo esto, tendremos la entrada de energía por la fuente E1 es igual a la entrada de energía al generador (Pig). Así que..,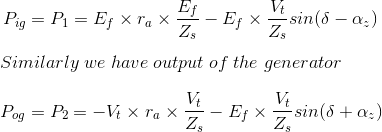
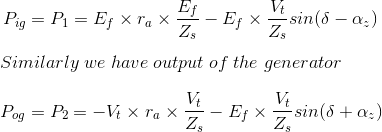
De manera similar tenemos la salida del generador
De estas ecuaciones se puede derivar un resultado importante. La diferencia entre la potencia de entrada al generador y la potencia de salida al generador da lugar a pérdidas óhmicas en el generador. Así que para probar la afirmación anterior restemos la potencia de salida de la potencia de entrada al generador: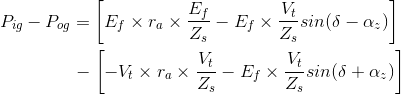
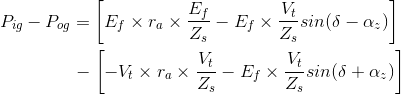
Al ampliar la expresión, tenemos![]()
![]()
En el diagrama de fáseres tenemos

Así que sustituyendo el valor, de esta ecuación tenemos

Normalmente descuidamos el valor de la resistencia de la armadura, debido a esto la z se convierte en cero y la Zs se convierte en igual a Xs. Por lo tanto, lo hemos hecho,![]()
![]()
Ahora estamos en condiciones de derivar la expresión para las condiciones de máxima potencia de salida del generador. Para derivar las condiciones de máxima potencia de salida, primero diferenciaremos la expresión de la ecuación de potencia de salida del generador que ya hemos deducido anteriormente, después de lo cual equipararemos la ecuación con cero. Al igualar con cero obtendremos la relación angular entre alfa y delta en condiciones de máxima potencia de salida. Matemáticamente tenemos L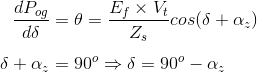
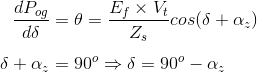
Esta es la condición necesaria para la máxima potencia de salida, a la máxima potencia de salida tenemos el ángulo de carga es igual al ángulo de impedancia.
Al sustituir la relación anterior en la relación de potencia de salida tenemos la potencia máxima de salida igual a![]()
![]()
Que es la expresión requerida para la máxima potencia de salida del generador.
Aquí estamos interesados en dibujar los diagramas de fáseres para la máxima potencia de salida en el caso del generador. A continuación se muestra el diagrama de los fáseres para el generador en caso de potencia máxima de salida. Todos los símbolos tienen sus significados habituales en el diagrama de fases.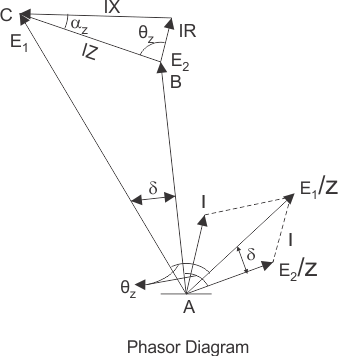

De manera similar, podemos derivar la expresión para la entrada máxima al generador. Para derivar las condiciones de máxima potencia de entrada, primero diferenciaremos la expresión de la ecuación de potencia de entrada del generador que ya hemos deducido anteriormente, después de lo cual equipararemos la ecuación con cero. Al igualar con cero obtendremos la relación angular entre el alfa y el delta en condiciones de máxima potencia de salida. Matemáticamente, tenemos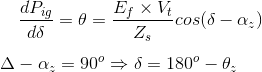
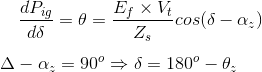
Esta es la condición requerida para la máxima entrada de energía, a la máxima entrada de energía tenemos el ángulo de carga es igual a los 180 grados menos el ángulo de impedancia. Al sustituir la relación anterior en la relación de potencia de entrada tenemos la máxima potencia de entrada igual a![]()
![]()
¿Cuál es la expresión requerida para la máxima potencia de entrada del generador?
Aquí, estamos interesados en dibujar los diagramas de fáseres para la máxima potencia de entrada en el caso del generador. A continuación se muestra el diagrama de los fáseres para el generador en caso de entrada de máxima potencia. Todos los símbolos tienen sus significados habituales en el diagrama de fases. Del diagrama fásico de máxima potencia de entrada podemos derivar varias condiciones para el factor de potencia y estas condiciones están escritas a continuación:
(a) Cuando (Efcos-Iaracos) es menor que el voltaje terminal, entonces el factor de potencia será mayor.
(b) Cuando (Efcos-Iaracos) es igual al voltaje terminal, entonces el factor de potencia será la unidad.
(c) Cuando (Efcos-Iaracos) es mayor que el voltaje terminal, entonces el factor de potencia se retrasará.
Derivemos ahora la expresión para Flujo de potencia reactiva en caso de generador síncrono. Podemos derivar la expresión de la potencia reactiva en el terminal de salida del generador como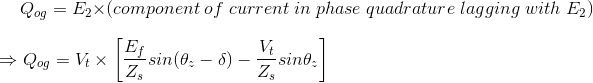
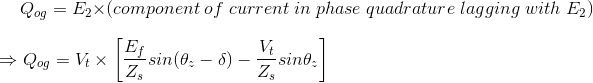
Además podemos escribir esta ecuación como![]()
![]()
De la ecuación anterior en el modo de generación si tenemos la resistencia de la armadura igual a cero entonces la ecuación anterior se reducirá a![]()
![]()
De la ecuación anterior podemos derivar varias condiciones para la factor de potencia y la potencia reactiva, estas condiciones están escritas a continuación:
(a) Cuando Efcos es menor que el voltaje terminal, entonces el factor de potencia será el principal y la potencia reactiva es negativa en el terminal de salida.
(b) Cuando Efcosis igual al voltaje terminal entonces el factor de potencia será unidad y la potencia reactiva es cero en el terminal de salida del generador.
(c) Cuando EfSi la tensión de la batería es mayor que la tensión en los terminales, el factor de potencia se retrasará y la potencia reactiva será positiva.
Ahora vamos a derivar varias ecuaciones para el flujo de energía del motor síncrono de rotor cilíndrico. Con el fin de derivar varias ecuaciones de potencia para un motor sincrónico sustituiremos la fuente de voltaje E1 igual al voltaje de excitación (Vt), fuente de tensión E2 es igual al voltaje terminal (Ef), la impedancia inductiva del circuito anterior es igual a la impedancia sincrónica (Zs) y Zs = ra + jXs. Después de reemplazar todo esto, tendremos la entrada de energía por la fuente E1 es igual a la entrada de energía al generador (Pig). Así que..,![]()
![]()
De manera similar tenemos la salida del motor sincrónico![]()
![]()
De estas ecuaciones se puede derivar un resultado importante. La diferencia entre la potencia de entrada al motor síncrono y la potencia de salida al motor síncrono da pérdidas óhmicas en el generador. Así que para probar la afirmación anterior restemos la potencia de salida de la potencia de entrada al motor síncrono: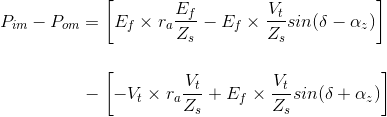
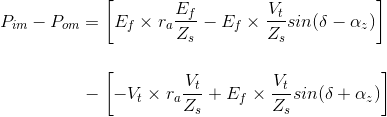
Al ampliar la expresión, tenemos![]()
![]()
En el diagrama de fáseres tenemos

Así que sustituyendo el valor, de esta ecuación que tenemos,

Normalmente descuidamos el valor de la resistencia de la armadura, debido a estoz se convierte en cero y Zs se convierte en igual a Xs. Por lo tanto, lo hemos hecho,![]()
![]()
Ahora estamos en condiciones de derivar la expresión para las condiciones de máxima potencia de salida para el motor sincrónico. Para derivar las condiciones de máxima potencia de salida, primero diferenciaremos la expresión de la ecuación de potencia de salida del motor síncrono que ya hemos deducido anteriormente, después de lo cual equipararemos la ecuación con cero. Al igualar con cero obtendremos la relación angular entre el alfa y el delta en condiciones de máxima potencia de salida. Matemáticamente tenemos L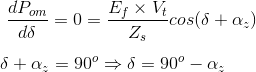
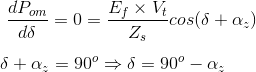
Esta es la condición necesaria para la máxima potencia de salida, a la máxima potencia de salida tenemos el ángulo de carga es igual al ángulo de impedancia. Al sustituir la relación anterior en la relación de potencia de salida tenemos la potencia máxima de salida igual a![]()
![]()
Que es la expresión requerida para la máxima potencia de salida del motor síncrono.
Aquí estamos interesados en dibujar los diagramas de fáseres para la máxima potencia de salida en caso de motor síncrono. A continuación se muestra el diagrama de fases del motor síncrono en caso de potencia máxima de salida. Todos los símbolos tienen su significado habitual en el diagrama de fases.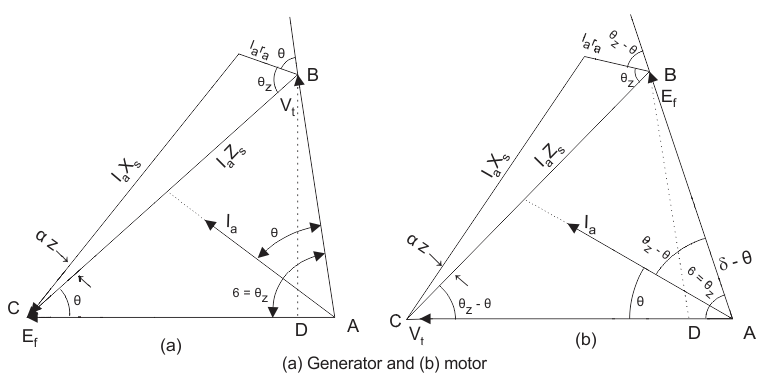

De manera similar, podemos derivar la expresión para la máxima entrada al motor. Para derivar las condiciones de entrada de máxima potencia, primero diferenciaremos la expresión de la ecuación de entrada de potencia del generador que ya hemos deducido anteriormente, después de lo cual equipararemos la ecuación con cero. Al igualar con cero obtendremos la relación angular entre el alfa y el delta en condiciones de máxima potencia de salida. Matemáticamente, tenemos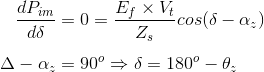
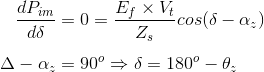
Esta es la condición requerida para la máxima entrada de energía, a la máxima entrada de energía tenemos el ángulo de carga es igual a los 180 grados menos el ángulo de impedancia.
Al sustituir la relación anterior en la relación de potencia de entrada tenemos la potencia máxima de entrada igual a![]()
![]()
Que es la expresión requerida para la máxima potencia de entrada para el motor sincrónico.
Aquí estamos interesados en dibujar los diagramas de fáseres para la máxima potencia de entrada en caso de motor síncrono. A continuación se muestra el diagrama de fases para el motor síncrono en caso de entrada de máxima potencia. Todos los símbolos tienen su significado habitual en el diagrama de fases.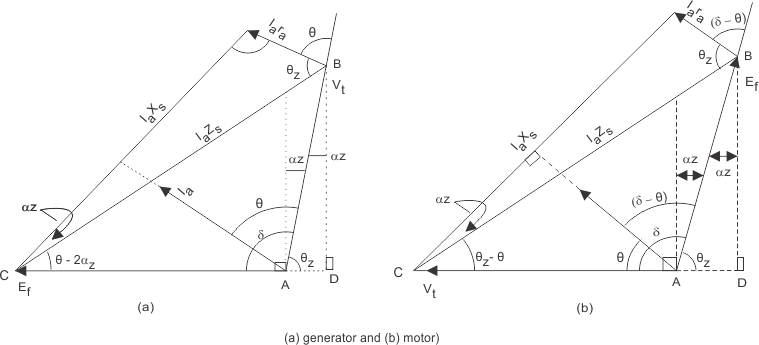

Del diagrama de fases de la máxima potencia de entrada podemos derivar varias condiciones para la factor de potencia y estas condiciones están escritas a continuación:
(a) Cuando (Efcos+Iaracos) es menor que la terminal voltaje …entonces el factor de potencia se debilitará.
(b) Cuando (Efcos+Iaracos) es igual al voltaje terminal, entonces el factor de potencia será la unidad.
(c) Cuando (Efcos+Iaracos) es mayor que el voltaje en los terminales, entonces el factor de potencia será mayor.
Derivemos ahora la expresión para el flujo de energía reactiva en caso de motor sincrónico. Podemos derivar la expresión para la potencia reactiva en el terminal de entrada del motor sincrónico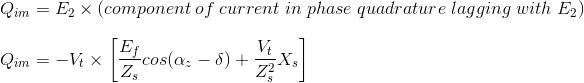
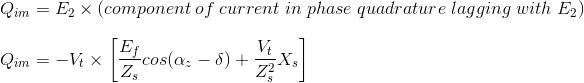
Además podemos escribir esta ecuación como![]()
![]()
De la ecuación anterior en el modo motorizado si tenemos la resistencia de la armadura igual a cero entonces la ecuación anterior se reducirá a![]()
![]()
De la ecuación anterior podemos derivar varias condiciones para el factor de potencia y la potencia reactiva, estas condiciones están escritas a continuación:
(a) Cuando Efporque es menos que terminal voltaje entonces el factor de potencia se retrasará y la potencia reactiva es positiva en el terminal de entrada.
(b) Cuando Efcos es igual a la tensión terminal, entonces el factor de potencia será la unidad y la potencia reactiva es cero en el terminal de entrada del motor sincrónico.
(c) Cuando EfSi la tensión de la red es mayor que la tensión en los terminales, el factor de potencia será mayor y la potencia reactiva será negativa.