A sistema de control es un sistema de dispositivos que gestiona, ordena, dirige o regula el comportamiento de otros dispositivos para conseguir un resultado deseado. En otras palabras, la definición de un sistema de control puede simplificarse como un sistema que controla otros sistemas para lograr un estado deseado. Hay varios tipos de sistemas de controlque puede ser categorizado en términos generales como sistemas de control lineal o sistemas de control no lineales. Estos tipos de sistemas de control se examinan en detalle a continuación.
Sistemas de control lineal
Con el fin de entender la sistema de control linealprimero debemos entender el principio de la superposición. El principio de teorema de superposición incluye dos de las propiedades importantes y se explican a continuación:
Homogeneidad: Se dice que un sistema es homogéneo, si multiplicamos la entrada por alguna constante A, la salida también se multiplicará por el mismo valor de la constante (es decir, A).
Aditividad: Supongamos que tenemos un sistema S y que estamos dando la entrada a este sistema como un1 por primera vez y estamos obteniendo la salida como b1 correspondiente a la entrada a1. En la segunda vez que estamos dando entrada a2 y en correspondencia con esto estamos obteniendo la salida como b2.
Ahora supongamos que esta vez estamos dando entrada como una suma de las entradas anteriores (es decir, un1 + a2) y que corresponden a esta entrada suponen que estamos obteniendo la salida como (b1 + b2) entonces podemos decir que el sistema S sigue la propiedad de la aditividad. Ahora somos capaces de definir el sistemas de control lineal como esos tipos de sistemas de control que siguen el principio de homogeneidad y aditividad.
Ejemplos de Sistema de Control Lineal
Considere una red puramente resistiva con una fuente constante de corriente continua. Este circuito sigue el principio de homogeneidad y aditividad. Todos los efectos no deseados son descuidados y asumiendo el comportamiento ideal de cada elemento de la red, decimos que obtendremos un comportamiento lineal voltaje y actual característica. Este es el ejemplo de una sistema de control lineal.
Sistemas de control no lineales
Podemos simplemente definir una sistema de control no lineal como un sistema de control que no sigue el principio de homogeneidad. En la vida real, todos los sistemas de control son sistemas no lineales (los sistemas de control lineales sólo existen en teoría). El describiendo la función es un procedimiento aproximado para analizar ciertos problemas de control no lineal.
Ejemplos de sistema no lineal
Un ejemplo bien conocido de un sistema no lineal es una curva de magnetización o la curva de no carga de una máquina de DC. Discutiremos brevemente la curva sin carga de las máquinas de corriente continua aquí: No curva de carga nos da la relación entre el flujo de la brecha de aire y el bobinado de campo mmf. Está muy claro en la curva que se da a continuación que en un principio, hay una relación lineal entre el devanado mmf y el flujo de la brecha de aire pero después de esto, ha llegado la saturación que muestra el comportamiento no lineal de la curva o las características del sistema de control no lineal.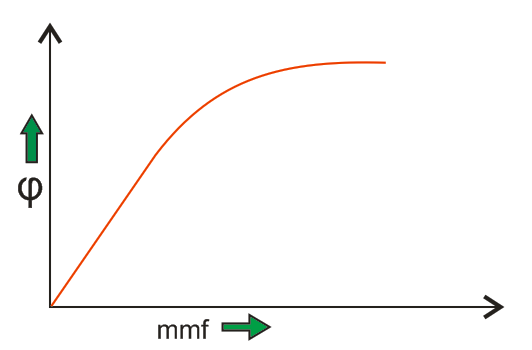

Sistema analógico o continuo
En estos tipos de sistemas de control, tenemos una señal continua como entrada al sistema. Estas señales son la función continua del tiempo. Podemos tener varias fuentes de señal de entrada continua como fuente de entrada de señal de tipo sinusoidal, fuente de entrada de señal de tipo cuadrado; la señal puede ser en forma de triángulo continuo, etc.
Sistema digital o discreto
En este tipo de sistemas de control, tenemos una señal discreta (o una señal que puede ser en forma de pulso) como entrada al sistema. Estas señales tienen un intervalo de tiempo discreto. Podemos convertir varias fuentes de señal de entrada continua como la fuente de entrada de señal de tipo sinusoidal, la fuente de entrada de señal de tipo cuadrado, etc., en una forma discreta utilizando el interruptor.
Ahora bien, hay varias ventajas del sistema discreto o digital sobre el sistema analógico y estas ventajas se escriben a continuación:
- Los sistemas digitales pueden manejar los sistemas de control no lineales con mayor eficacia que los sistemas de tipo analógico.
- Las necesidades de energía en caso de un sistema discreto o digital son menores en comparación con los sistemas analógicos.
- El sistema digital tiene una mayor tasa de precisión y puede realizar varios cálculos complejos fácilmente en comparación con los sistemas analógicos.
- La fiabilidad del sistema digital es mayor que la de un sistema analógico. También tienen un tamaño pequeño y compacto.
- El sistema digital trabaja en las operaciones lógicas lo que aumenta su precisión muchas veces.
- Las pérdidas en caso de sistemas discretos son menores en comparación con los sistemas analógicos en general.
Sistemas de una sola entrada y una sola salida
Estos también son conocidos como SISO tipo de sistema. En éste, el sistema tiene una sola entrada para una sola salida. Varios ejemplos de este tipo de sistema pueden incluir el control de la temperatura, el sistema de control de posición, etc.
Sistemas de entrada múltiple y salida múltiple
Estos también son conocidos como sistemas del tipo MIMO. En éste, el sistema tiene múltiples salidas para múltiples entradas. Varios ejemplos de este tipo de sistema pueden incluir el sistema de tipo PLC, etc.
Sistema de parámetros agrupados
En estos tipos de sistemas de control, los diversos componentes activos y pasivos se supone que se concentran en un punto y por eso se llaman sistemas de tipo de parámetros agrupados. El análisis de este tipo de sistema es muy fácil e incluye ecuaciones diferenciales.
Sistema de parámetros distribuidos
En estos tipos de sistemas de control, los diversos activos (como inductores y condensadores) y los parámetros pasivos (resistencia) se supone que están distribuidos uniformemente a lo largo de la longitud y es por eso que se denominan tipo de sistema de parámetros distribuidos. El análisis de este tipo de sistema es ligeramente difícil, ya que incluye ecuaciones diferenciales parciales.