Ya hemos discutido el Series de Fourier en forma exponencial. En este artículo discutiremos otra forma de las series de Fourier, es decir. Serie de Fourier trigonométrica.
Representación de series de Fourier en forma trigonométrica
Las series de Fourier en forma trigonométrica puede derivarse fácilmente de su forma exponencial. La representación de la compleja serie exponencial de Fourier de una señal periódica x(t) con el período fundamental To está dada por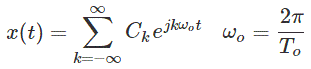
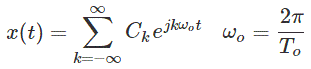
Dado que el seno y el coseno pueden expresarse en forma exponencial. Así, manipulando las series exponenciales de Fourier, podemos obtener su forma trigonométrica.
El series de Fourier trigonométricas La representación de una señal periódica x (t) con el período fundamental T, viene dada por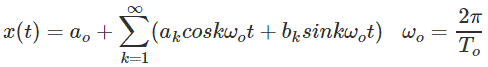
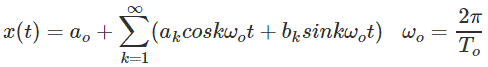
Donde unk y bk son los coeficientes de Fourier dados por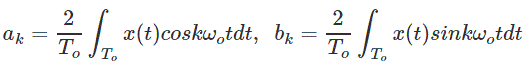
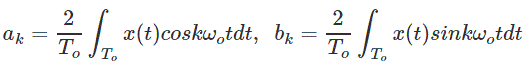
a0 es el componente de cc de la señal y está dada por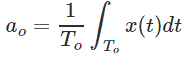
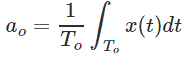
Propiedades de las series de Fourier
1. Si x(t) es una función uniforme es decir, x(- t) = x(t), entonces bk = 0 y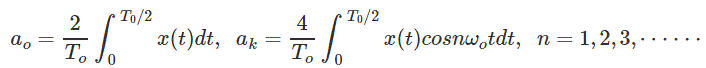
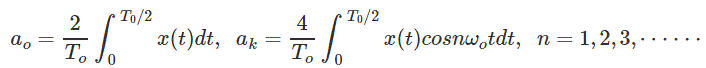
2. Si x(t) es una función uniforme es decir, x(- t) = x(t), entonces a0 = 0, ak = 0 y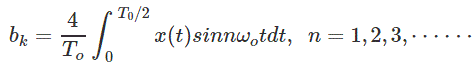
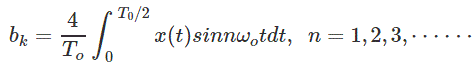
3. Si x(t) es la mitad de la función simétrica es decir, x (t) = -x(t T)0/2), entonces a0 = 0, ak = bk = 0 para k incluso,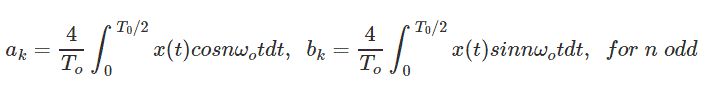
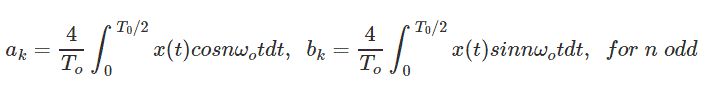
4. Linearidad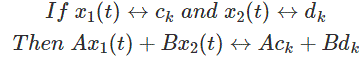
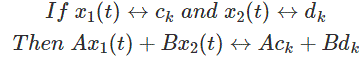
5. El cambio de tiempo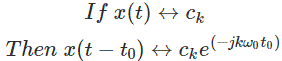
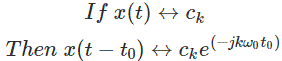
6. Inversión del tiempo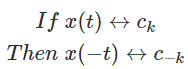
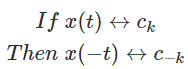
7. Multiplicación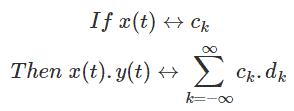
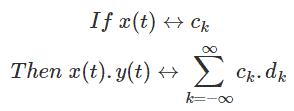
8. Conjugación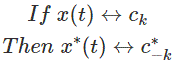
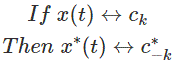
9. Diferenciación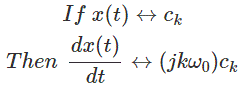
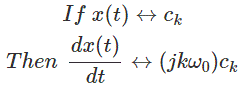
10. Integración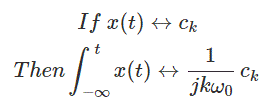
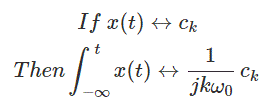
11. Convolución periódica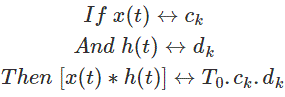
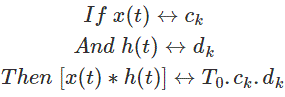
Relación entre los coeficientes de la forma exponencial y los coeficientes de la forma trigonométrica
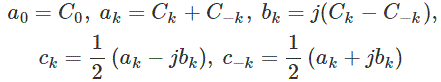
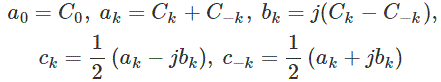
Cuando x (t) es real, entonces a, y b, son reales, tenemos![]()
![]()
Efecto del desplazamiento del eje de la señal
- Al desplazar la forma de onda hacia la derecha izquierda con respecto al eje temporal de referencia t = 0, sólo cambian los valores de fase del espectro, pero el espectro de magnitud permanece igual.
- Al desplazar la forma de onda hacia arriba o hacia abajo el eje de tiempo w.r.t. cambia sólo el valor DC de la función.