A árbol de la red eléctrica es un conjunto de ramas que contiene todos los nodos de la red pero no forma ningún camino cerrado. Es similar a lo que un topología de la red es a una red de comunicaciones.
Expliquemos el árbol de la red eléctrica como se ha definido anteriormente.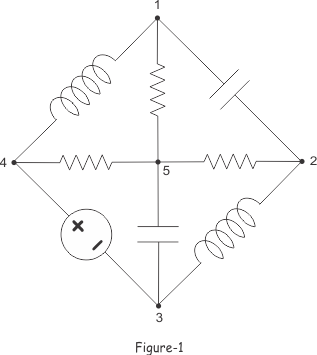

La anterior figura-1, muestra una red eléctrica con cinco nodos 1,2,3,4 y 5.
Ahora, si quitamos las ramas 1-2, 2-3, 3-4 y 4-1 del circuito, obtendremos, el gráfico como se muestra abajo en la figura-2.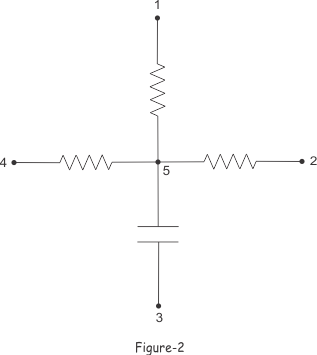

El gráfico anterior, como se muestra en la figura-2, contiene los cinco nodos de la red, pero no de ningún camino cerrado. Este es un ejemplo de árbol de la red eléctrica.
De esta manera, los números de este árbol pueden formarse en un solo El circuito eléctrico…que contiene los mismos cinco nodos sin contener ningún bucle cerrado.
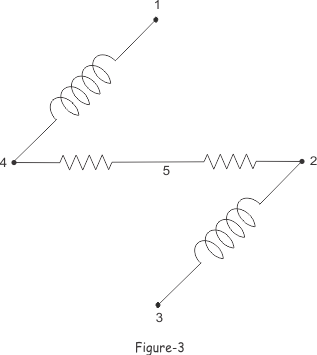

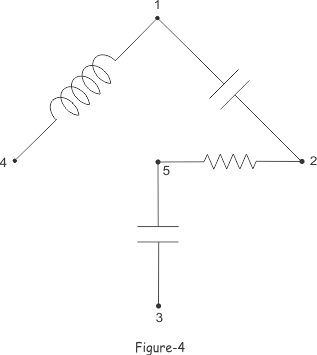

Las ramas de un árbol también se conocen como ramitas.
En las figuras 2, 3 y 4 podemos ver que hay cuatro ramas de árbol en cada árbol de esa red eléctrica. El número de nodos en la red es de 5.
Así que, en este caso,![]()
![]()
Esta es una ecuación general para todos los árboles de cualquier red eléctrica. La ecuación general se escribe normalmente como,
Donde, l es el número de ramas de un árbol y n es el número de nodos de la red de la que se forman los árboles.
Árboles de la red eléctrica
Cuando se forma un gráfico de una red eléctrica, se toman algunas ramas selectivas. Las ramas de la red que no están en formación de árbol se denominan enlaces o acordes. El gráfico formado por estos eslabones o acordes se llama cotree. El árbol puede cerrarse o abrirse dependiendo de los eslabones.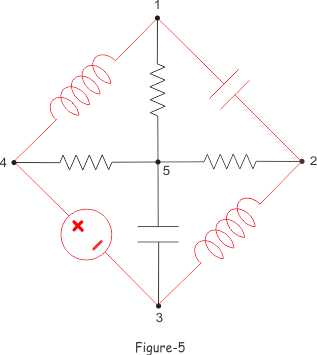

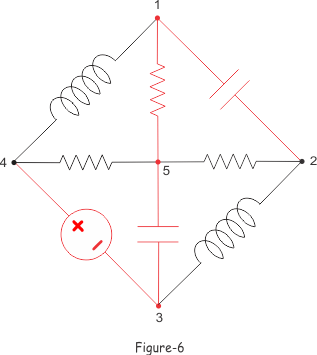

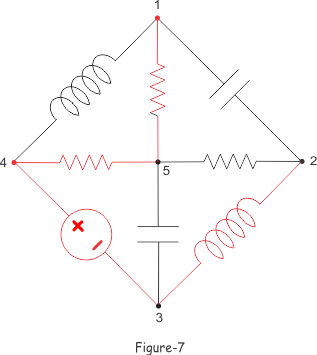

Los árboles se muestran en las figuras anteriores por el color rojo. En la figura 5, la figura 6 y la figura 7 se encuentra que la suma del número de ramas de un árbol y su árbol es el número total de ramas de la red eléctrica.
Así que, si el número de enlaces de un árbol es l, entonces
Donde, l es el número de ramitas en el árbol y b es el número de ramas en una red. Así que,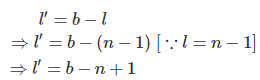
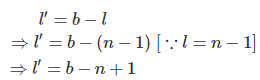
Donde, n es el número de nodos en la red eléctrica.
Propiedades del Árbol de la Red Eléctrica
- Un árbol consiste en todos los nodos de la red eléctrica.
- Un árbol tiene el número de ramas que es menos de 1 del número de nodos de la red eléctrica.
- Un árbol no debe tener ningún camino cerrado en ninguna parte de él.
- Puede haber muchos árboles diferentes posibles en la misma red eléctrica.
- La suma del número de ramas de un árbol y el número de ramas de su árbol es igual al número total de ramas de su red eléctrica.
- El número de independientes Ley de tensión de Kirchhoff se pueden formar ecuaciones para que una red eléctrica sea igual a su número de enlaces o acordes de cotree.
- El número de independientes Ley actual de Kirchhoff se pueden formar ecuaciones para que una red eléctrica sea igual al número de ramitas



