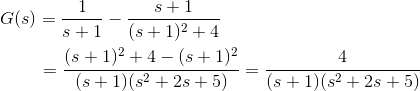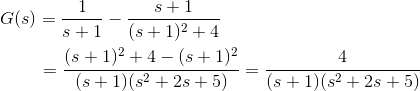A función de transferencia representa la relación entre la señal de salida de un sistema de control y la señal de entrada, para todos los posibles valores de entrada. Un diagrama de bloques es una visualización del sistema de control que utiliza bloques para representar la función de transferencia, y flechas que representan las diversas señales de entrada y salida.
Para cualquier sistema de control, existe una entrada de referencia conocida como excitación o causa que opera a través de una operación de transferencia (es decir, la función de transferencia) para producir un efecto que resulta en una salida o respuesta controlada.
Así pues, la relación de causa y efecto entre la salida y la entrada se relaciona entre sí mediante una función de transferencia.![]()
![]()
En un Laplace Transformarsi la entrada está representada por R(s) y la salida por C(s), entonces la función de transferencia será:![]()
![]()
Es decir, la función de transferencia del sistema multiplicada por la función de entrada da la función de salida del sistema.
¿Qué es una función de transferencia
La función de transferencia de un sistema de control se define como la relación entre la transformación Laplace de la variable de salida y la transformación Laplace de la variable de entrada, suponiendo que todas las condiciones iniciales sean cero.![]()
![]()
El procedimiento para determinar la función de transferencia de un sistema de control es el siguiente:
- Formamos las ecuaciones para el sistema.
- Ahora tomamos la transformación de Laplace de las ecuaciones del sistema, asumiendo las condiciones iniciales como cero.
- Especifique la salida y entrada del sistema.
- Por último, tomamos la relación de la transformación Laplace de la salida y la transformación Laplace de la entrada que es la función de transferencia requerida.
No es necesario que la salida y la entrada de un sistema de control sean de la misma categoría. Por ejemplo, en motores eléctricos la entrada es una señal eléctrica mientras que la salida es una señal mecánica ya que la energía eléctrica necesaria para hacer girar los motores. De manera similar, en un generador eléctrico, la entrada es una señal mecánica y la salida es una señal eléctrica, ya que se requiere energía mecánica para producir electricidad en un generador.
Pero para el análisis matemático, de un sistema todo tipo de señales deben ser representadas en una forma similar. Esto se hace transformando todo tipo de señales a su forma de Laplace. También la función de transferencia de un sistema se representa en forma Laplace dividiendo la función de transferencia Laplace de salida a la función de transferencia Laplace de entrada. Por lo tanto, un diagrama de bloques básico de un sistema de control puede ser representado como![]()
![]()
![]()
![]()
Donde r(t) y c(t) son función del dominio del tiempo de la señal de entrada y de salida respectivamente.
Métodos para obtener una función de transferencia
Hay dos formas principales de obtener una función de transferencia para el sistema de control. Las formas son:
- Método del diagrama de bloques: No es conveniente derivar una función de transferencia completa para un sistema de control complejo. Por lo tanto, la función de transferencia de cada elemento de un sistema de control está representada por un diagrama de bloques. Se aplican técnicas de reducción del diagrama de bloques para obtener la función de transferencia deseada.
- Gráficos de flujo de señales: La forma modificada de un diagrama de bloques es una gráfico de flujo de señales. El diagrama de bloques da una representación pictórica de un sistema de control. El gráfico de flujo de señales acorta aún más la representación de un sistema de control.
Polos y ceros de la función de transferencia
Generalmente, una función puede ser representada en su forma polinómica. Por ejemplo,

Ahora, de manera similar, la función de transferencia de un sistema de control también puede representarse como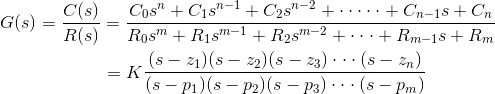
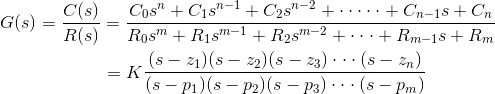
Donde K se conoce como el factor de ganancia de la función de transferencia.
Ahora en la función anterior si s = z1o s = z2o s = z3,.s = znel valor de la función de transferencia se convierte en cero. Estos z1, z2, z3,.znson raíces del polinomio numerador. En cuanto a estas raíces del polinomio numerador, la función de transferencia se convierte en cero, estas raíces se llaman ceros de la función de transferencia.
Ahora, si s = p1o s = p2o s = p3,.s = pmel valor de la función de transferencia se vuelve infinito. Por lo tanto, las raíces del denominador se llaman los polos de la función.
Ahora reescribamos la función de transferencia en su forma polinómica.![]()
![]()
Ahora, consideremos s aproximaciones al infinito ya que las raíces son todas finitas, pueden ser ignoradas comparadas con el infinito s. Por lo tanto![]()
![]()
Por lo tanto, cuando s y n > m, la función tendrá también valor de infinito, es decir, la función de transferencia tiene polos en el infinito s, y la multiplicidad u orden de tales polos es n m.
De nuevo, cuando s y n < m, la función de transferencia tendrá valor cero, lo que significa que la función de transferencia tiene ceros en el infinito s, y la multiplicidad u orden de tales ceros es m n.
Concepto de la función de transferencia
La función de transferencia se expresa generalmente en la Transformada Laplace y no es más que la relación entre la entrada y la salida de un sistema. Consideremos que un sistema consiste en una serie conectada resistencia (R) y inductancia (L) a través de un fuente de tensión (V).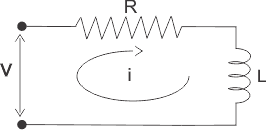

En este circuito, la corriente i es la respuesta debida a la aplicación voltaje (V) como causa. Por lo tanto, el voltaje y actual del circuito pueden considerarse como entrada y salida del sistema respectivamente.
Del circuito, tenemos,![]()
![]()
Ahora aplicando la Transformación Laplace, tenemos,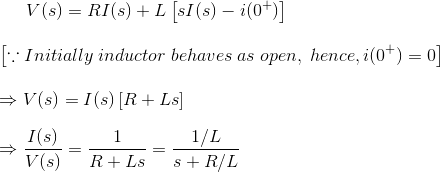
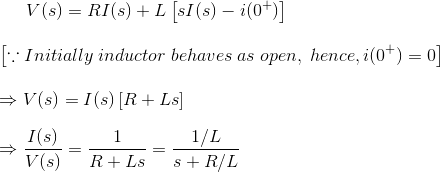
La función de transferencia del sistema, G(s) = I(s)/V(s), la relación entre la salida y la entrada.
1) Expliquemos el concepto de polos y ceros de la función de transferencia a través de un ejemplo.![]()
![]()
Solución
Los ceros de la función son, -1, -2 y los polos de las funciones son -3, -4, -5, -2 + 4j, -2 4j.
Aquí n = 2 y m = 5, ya que n < m y m n = 3, la función tendrá 3 ceros en s . Los polos y los ceros se representan en la siguiente figura 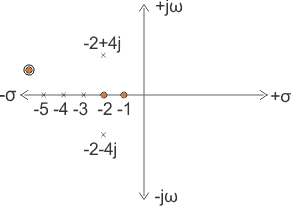

2) Tomemos otro ejemplo de la función de transferencia del sistema de control![]()
![]()
Solución
En la función de transferencia anterior, si el valor del numerador es cero, entonces![]()
![]()
Estos son la ubicación de los ceros de la función.
De manera similar, en la función de transferencia anterior, si el valor del denominador es cero, entonces![]()
![]()
Estos son la ubicación de los polos de la función.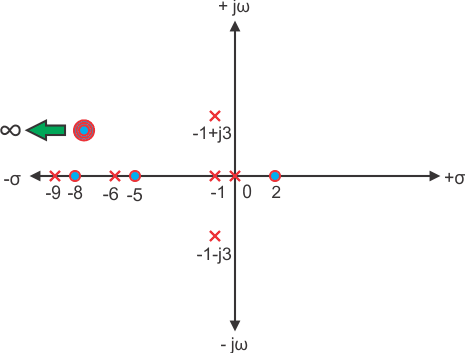

Como el número de ceros debe ser igual al número de polos, los tres ceros restantes se encuentran en s .
Ejemplo de la función de transferencia de una red
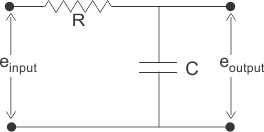
3)

Solución
En la red anterior es obvio que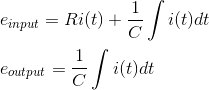
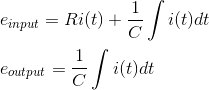
Supongamos,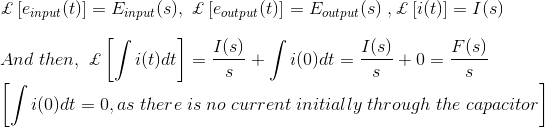
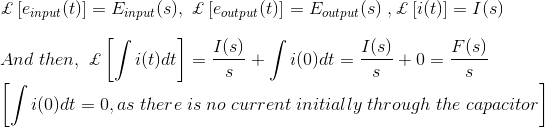
Tomando la transformación de Laplace de las ecuaciones anteriores con la consideración de la condición inicial como cero, obtenemos,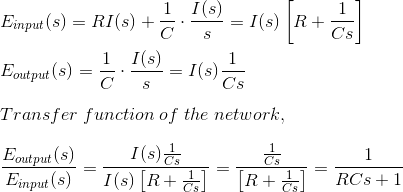
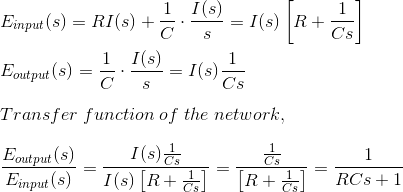
El efecto de la señal de impulso
La señal de impulso unitario se define como![]()
![]()


La transformación de la función de impulso de la unidad es 1.

Ahora, si la señal de entrada es una señal de impulso unitario, entonces,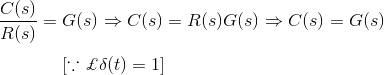
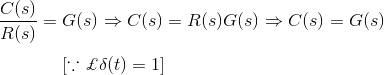
La función de salida es la misma que su función de transferencia.
Ejemplo de función de transferencia
1) La respuesta de impulso de un sistema es

¿Cuál será la función de transferencia del sistema?
Solución
Para la respuesta al impulso, la salida C(s) del sistema es igual a la función de transferencia del sistema.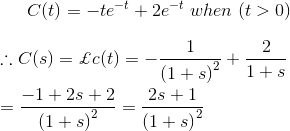
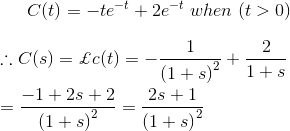
Por lo tanto, la función de transferencia del sistema es![]()
![]()
2) Encontrar los polos y ceros de la función![]()
![]()
Solución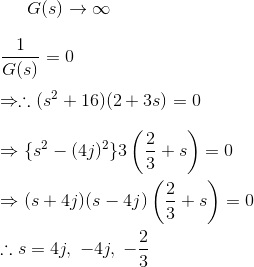
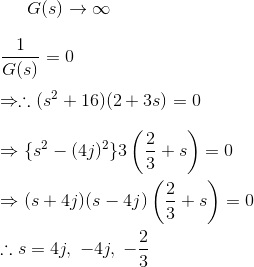
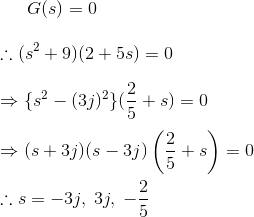
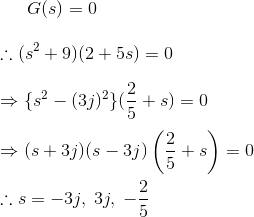
3) Los polos y los ceros están trazados en la llanura como se muestra a continuación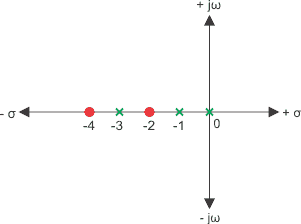

Encuentra la función de transferencia.
Solución
Aquí, los polos son s = 3, 1, 0.
Por lo tanto, el denominador de la función sería,

los ceros son, -4, 2.
Por lo tanto, el numerador de la función sería,

Por lo tanto, la función de transferencia sería,![]()
![]()
Donde, K es el factor de ganancia del sistema de control.
4) Encuentra el factor de ganancia K de una función de transferencia cuyo valor es 2 en s = 2 y la función de transferencia se da como![]()
![]()
Solución
Ahora, según la condición del problema,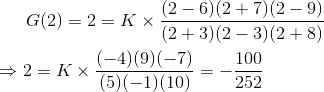
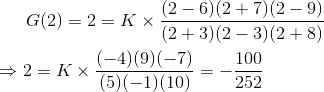
5) Encuentra la función de transferencia de la siguiente red.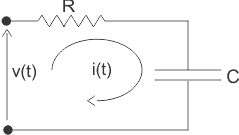

Solución
Del circuito que tenemos,![]()
![]()
Ahora se aplica La transformación de Laplace en ambos lados que tenemos,![]()
![]()
Como el aplicado voltaje es la causa y la correspondiente carga actual es el efecto, el voltaje aplicado puede considerarse como entrada y la corriente de carga puede considerarse como salida.![]()
![]()
6) Encuentra la función de transferencia de la red que se indica a continuación,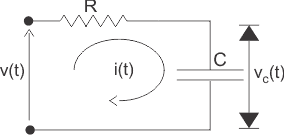

Solución
En la figura anterior, la entrada es el voltaje aplicado v(t) y la salida se mide como el voltaje aparece a través de la condensador C que es vc(t).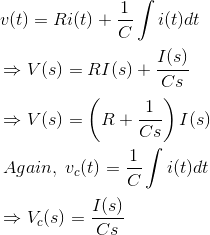
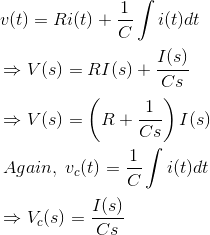
La transformación de Laplace de la función de transferencia es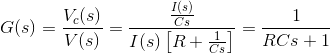
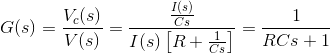
7) Un eje de interior J se gira para un ángulo debido a la torsión aplicada T contra una fricción de cojinete f. Encuentra la función de transferencia del sistema.
Solución
La forma de ecuación diferencial de la declaración anterior es![]()
![]()
Tomando la transformación de Laplace de ambos lados del sistema,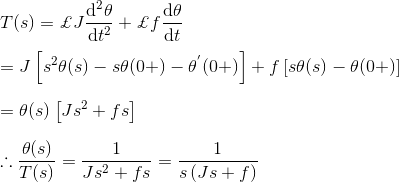
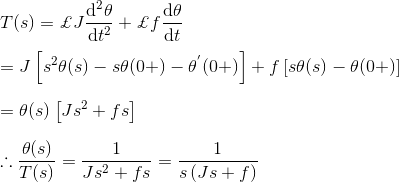
Como el par aplicado es de entrada y el desplazamiento angular de salida es de salida del sistema.
8) La respuesta de impulso del sistema viene dada por c(t) = 1 te-2t + sin3t. Encuentra esa función de transferencia del sistema
Solución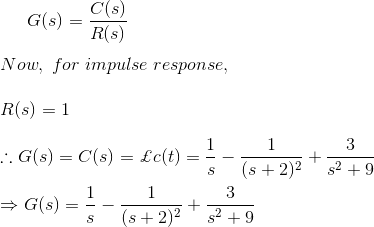
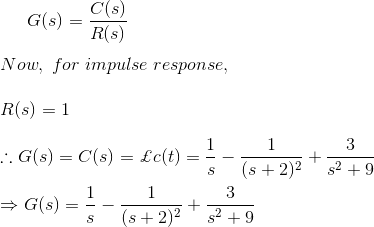
9) Encuentra la función de transferencia de la respuesta de impulso de un sistema dada por

Solución