Sabemos que cuando un motor eléctrico y la unidad funciona, hay una generación de calor dentro del motor. La cantidad de calor generada dentro del motor debe ser conocida con la mayor precisión posible. Por eso modelado térmico del motor es necesario. El material de los motores y la forma y tamaño de los mismos no son únicos, pero la generación de calor no se altera mucho dependiendo de estas características. Por lo tanto, un modelo térmico simple de cualquier motor se puede obtener asumiendo que es un cuerpo homogéneo. El objetivo principal de este modelado es elegir la potencia adecuada de un motor para que el motor eléctrico no excede su límite de seguridad durante la operación.
En el tiempo t, dejemos que el motor tenga los siguientes parámetros
p1 = Calor desarrollado, en julios/segundo o vatios
p2 = Calor disipado al medio de enfriamiento, vatios
W = Peso de las partes activas de la máquina.
h = Calor específico, Jules por Kg por oC.
A = Superficie de enfriamiento, m2
d = Coeficiente de transferencia de calor, Joules/Sec/m2/oC
= Aumento de la temperatura media oC
Ahora, si el tiempo dt, que el aumento de la temperatura de la máquina sea d,
Por lo tanto, el calor absorbido en la máquina = (El calor generado en el interior de la máquina El calor se disipó a la medicina de refrigeración circundante)
Donde, d = p1dt p2dt.(i)
Ya que, p2 = dA.(ii)
Sustituyendo (ii) en (i), obtenemos![]()
![]()
Aquí, C se llama la capacidad térmica de la máquina en vatios.oC y D es la constante de disipación de calor en vatios.oC.
Cuando adquirimos la ecuación diferencial de primer orden de la ecuación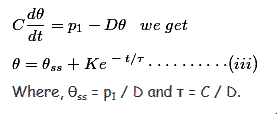
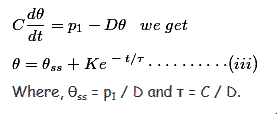
Obtenemos el valor de K poniendo t = 0 en la ecuación (iii) y obtenemos la solución como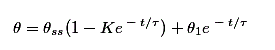
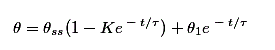
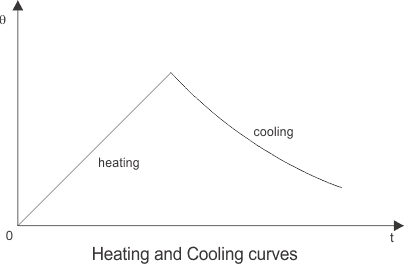
Así, a partir de la ecuación anterior podemos averiguar el aumento de la temperatura dentro de una máquina en funcionamiento, que está muy cerca de ser exacta y si trazamos un gráfico para la variación del riesgo de temperatura con el tiempo durante el calentamiento y el enfriamiento y por lo tanto el modelado térmico de un motor se completa.