

Este teorema fue introducido en el año 1952 por el ingeniero eléctrico holandés Bernard D.H. Tellegen. Este es un teorema muy útil en el análisis de redes. De acuerdo con Teorema de Tellegenla suma de las potencias instantáneas para el número n de ramas de una red eléctrica es cero. ¿Está confundido? Expliquémoslo. Supongamos que n número de ramas en una red eléctrica tiene i1, i2, i3, . in respectivas corrientes instantáneas a través de ellos. Estas corrientes satisfacen Ley actual de Kirchhoffs.
De nuevo, supongamos que estas ramas tienen voltajes instantáneos a través de ellas son v1, v2, v3, .. vn respectivamente. Si estos voltajes a través de estos elementos satisfacen Ley de tensión de Kirchhoff entonces,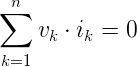
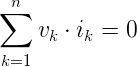
vk es la instantánea voltaje a través de la kth branch y yok es la corriente instantánea que fluye a través de esta rama. Teorema de Tellegen es aplicable a redes agrupadas que consisten en redes lineales, no lineales, variantes de tiempo, variantes de tiempo y elementos activos y pasivos.
Este teorema puede explicarse fácilmente con el siguiente ejemplo.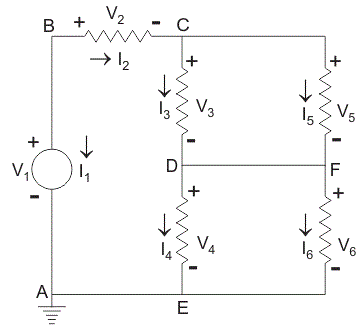

En la red mostrada, se han seleccionado direcciones de referencia arbitrarias para todas las corrientes de rama, y se han indicado las correspondientes tensiones de rama, con una dirección de referencia positiva en la cola de la actual flecha.
Para esta red, asumiremos que un conjunto de voltajes de rama satisfacen la ley de voltaje de Kirchhoff y un conjunto de corriente de rama satisface la ley de corriente de Kirchhoff en cada nodo.
Entonces mostraremos que estos voltajes y corrientes arbitrarias asumidas satisfacen la ecuación.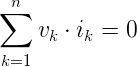
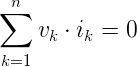
Y es la condición de Teorema de Tellegen.
En la red que se muestra en la figura, dejemos que v1, v2 y v3 ser de 7, 2 y 3 voltios respectivamente. Aplicando Ley de tensión de Kirchhoff alrededor del bucle ABCDEA. Vemos que v4 = Se requieren 2 voltios. Alrededor del bucle CDFC, v5 se requiere que sea de 3 voltios y alrededor del bucle DFED, v6 se requiere que sea 2. A continuación aplicamos Ley actual de Kirchhoffs sucesivamente a los nodos B, C y D.
En el nodo B deja quei = 5 A, entonces se requiere que i2 = 5 A. En el nodo C deja i3 = 3 A y luego i5 se requiere que sea de 8. En el nodo D ssume i4 para tener 4 años, entonces yo6 se requiere que tenga 9 años. Llevar a cabo la operación de la ecuación,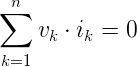
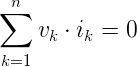
Lo conseguimos,
Por lo tanto Teorema de Tellegen se verifica.
