Ahora estamos familiarizados con los fundamentos de varios sistemas de números usados en electrónica digital. Ahora vamos a mirar rápidamente a través del sistema de números principales que es sistema numérico binario. En el sistema numérico binario 0 y 1 pueden representar todos los números. Antes de discutir sobre 1s complemento veamos primero algunas cosas diferentes.
Veamos los números del 0 al 7


Ahora hemos dado esto como ejemplo para ilustrar la representación de los números binarios. Esto se hace para representar los números positivos. ¿Pero qué pasa si queremos representar los números negativos en el sistema numérico binario.
El concepto de signo negativo no existe en el sistema numérico binario. Aunque ha habido disputas sobre la representación de los números negativos en el sistema numérico binario. Y para ello se han desarrollado varios métodos. Los más populares de todos ellos son 1s complemento y 2s complemento. Aunque 2s complemento domina el complemento 1s en popularidad, pero también se utiliza debido a un diseño algo más simple en el hardware debido a un concepto más simple. Ahora veremos el método del complemento 1s.
Representación numérica
El complemento 1s es un método muy fácil para representar números negativos en el sistema numérico binario. Para representar cualquier número que sea negativo primero tenemos que considerar el valor binario de su magnitud positiva en el sistema binario, luego tenemos que simplemente convertir los 1s con 0 y los 0s con 1 y obtendremos el complemento de 1s de ese número que es también el valor negativo de ese número. Como podemos ver, este método es realmente un método de complementación. Tendremos una idea clara si miramos algunos ejemplos.


Ejemplo
Primero consideremos los números positivos de 0 -7


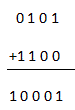
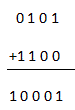
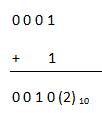
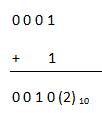
Ahora el 1s complemento de estos números será como sigue
Sustracción utilizando el complemento 1s
El método de sustracción binaria se vuelve muy fácil con la ayuda del complemento 1s. Ahora veamos un ejemplo para entender la resta con la ayuda del complemento 1s.
Supongamos que A = (5)10 = (0 1 0 1)2
Y B = (3)10 = (0 0 1 1)2
Y queremos averiguar que A B
Para esto primero tenemos que calcular 1s complemento de B
1s complemento de B = 1 1 0 0
Ahora tenemos que sumar el resultado con A
Ahora en el resultado podemos ver que hay un bit desbordante que tenemos que añadir con el resultado restante
Este es el resultado deseado.
Y cuando no haya ningún dígito desbordante, el resultado obtenido en la etapa anterior será la respuesta.